mirror of
https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git
synced 2024-12-27 15:41:16 +08:00
Merge branch 'master' into improve-bubble-sort
This commit is contained in:
commit
07f5ecf025
@ -10,6 +10,8 @@ Each algorithm and data structure have its own separate README
|
||||
with related explanations and links for further reading and YouTube
|
||||
videos.
|
||||
|
||||
Read this in other languages: [Chinese](https://github.com/trekhleb/javascript-algorithms/blob/master/README.zh-CN.md)
|
||||
|
||||
## Data Structures
|
||||
|
||||
Data structure is a particular way of organizing and storing data in a computer so that it can
|
||||
@ -190,7 +192,7 @@ Below is the list of some of the most used Big O notations and their performance
|
||||
| **O(1)** | 1 | 1 | 1 |
|
||||
| **O(log N)** | 3 | 6 | 9 |
|
||||
| **O(N)** | 10 | 100 | 1000 |
|
||||
| **O(N log N)** | 30 | 60 | 9000 |
|
||||
| **O(N log N)** | 30 | 600 | 9000 |
|
||||
| **O(N^2)** | 100 | 10000 | 1000000 |
|
||||
| **O(2^N)** | 1024 | 1.26e+29 | 1.07e+301 |
|
||||
| **O(N!)** | 3628800 | 9.3e+157 | 4.02e+2567 |
|
||||
|
||||
212
README.zh-CN.md
Normal file
212
README.zh-CN.md
Normal file
@ -0,0 +1,212 @@
|
||||
# JavaScript 算法与数据结构
|
||||
|
||||
[](https://travis-ci.org/trekhleb/javascript-algorithms)
|
||||
[](https://codecov.io/gh/trekhleb/javascript-algorithms)
|
||||
|
||||
本仓库包含了多种基于 JavaScript 的算法与数据结构。
|
||||
|
||||
每种算法和数据结构都有自己的 README 并提供相关说明以及进一步阅读和 YouTube 视频。
|
||||
|
||||
## 数据结构
|
||||
|
||||
数据结构是在计算机中组织和存储数据的一种特殊方式,它可以高效地访问和修改数据。更确切地说,数据结构是数据值的集合,它们之间的关系、函数或操作可以应用于数据。
|
||||
|
||||
* [链表](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/linked-list)
|
||||
* [队列](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/queue)
|
||||
* [栈](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/stack)
|
||||
* [哈希表](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/hash-table)
|
||||
* [堆](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/heap)
|
||||
* [优先队列](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/priority-queue)
|
||||
* [字典树](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/trie)
|
||||
* [树](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/tree)
|
||||
* [二分查找](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/tree/binary-search-tree)
|
||||
* [AVL 树](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/tree/avl-tree)
|
||||
* 红黑树
|
||||
* 后缀树
|
||||
* 线段树 或 间隔树
|
||||
* 二叉索引树
|
||||
* [图](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/graph) (有向图与无向图)
|
||||
* [并查集](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/disjoint-set)
|
||||
|
||||
## 算法
|
||||
|
||||
算法是如何解决一类问题的明确规范。 算法是一组精确定义操作序列的规则。
|
||||
|
||||
### 算法主题
|
||||
|
||||
* **数学**
|
||||
* [阶乘](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/factorial)
|
||||
* [斐波那契数](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/fibonacci)
|
||||
* [素数检测](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/primality-test) (排除法)
|
||||
* [欧几里得算法](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/euclidean-algorithm) - 计算最大公约数(GCD)
|
||||
* [最小公倍数](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/least-common-multiple) (LCM)
|
||||
* [整数拆分](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/integer-partition)
|
||||
* **集合**
|
||||
* [笛卡尔积](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/cartesian-product) - 多集合结果
|
||||
* [幂集](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/power-set) - 该集合的所有子集
|
||||
* [排列](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/permutations) (有/无重复)
|
||||
* [组合](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/combinations) (有/无重复)
|
||||
* [洗牌算法](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/fisher-yates) - 随机置换有限序列
|
||||
* [最长公共子序列](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/longest-common-subsequnce) (LCS)
|
||||
* [最长递增子序列](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/longest-increasing-subsequence)
|
||||
* [Shortest Common Supersequence](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/shortest-common-supersequence) (SCS)
|
||||
* [背包问题](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/knapsack-problem) - "0/1" and "Unbound" ones
|
||||
* [最大子数列问题](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/maximum-subarray) - BF算法 与 动态编程
|
||||
* **字符串**
|
||||
* [莱温斯坦距离](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/string/levenshtein-distance) - 两个序列之间的最小编辑距离
|
||||
* [汉明距离](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/string/hamming-distance) - 符号不同的位置数
|
||||
* [克努斯-莫里斯-普拉特算法](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/string/knuth-morris-pratt) - 子串搜索
|
||||
* [字符串快速查找](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/string/rabin-karp) - 子串搜索
|
||||
* [最长公共子串](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/string/longest-common-substring)
|
||||
* **搜索**
|
||||
* [二分查找](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/search/binary-search)
|
||||
* **排序**
|
||||
* [冒泡排序](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sorting/bubble-sort)
|
||||
* [选择排序](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sorting/selection-sort)
|
||||
* [插入排序](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sorting/insertion-sort)
|
||||
* [堆排序](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sorting/heap-sort)
|
||||
* [归并排序](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sorting/merge-sort)
|
||||
* [快速排序](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sorting/quick-sort)
|
||||
* [希尔排序](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sorting/shell-sort)
|
||||
* **树**
|
||||
* [深度优先搜索](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/tree/depth-first-search) (DFS)
|
||||
* [广度优先搜索](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/tree/breadth-first-search) (BFS)
|
||||
* **图**
|
||||
* [深度优先搜索](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/depth-first-search) (DFS)
|
||||
* [广度优先搜索](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/breadth-first-search) (BFS)
|
||||
* [戴克斯特拉算法m](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/dijkstra) - 找到所有图顶点的最短路径
|
||||
* [贝尔曼-福特算法](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/bellman-ford) - 找到所有图顶点的最短路径
|
||||
* [判圈算法](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/detect-cycle) - 对于有向图和无向图(基于DFS和不相交集的版本)
|
||||
* [普林演算法](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/prim) - 寻找加权无向图的最小生成树(MST)
|
||||
* [克鲁斯克尔演算法](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/kruskal) - 寻找加权无向图的最小生成树(MST)
|
||||
* [拓撲排序](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/topological-sorting) - DFS 方法
|
||||
* [关节点](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/articulation-points) - Tarjan算法(基于DFS)
|
||||
* [桥](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/bridges) - 基于DFS的算法
|
||||
* [欧拉路径与一笔画问题](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/eulerian-path) - Fleury的算法 - 一次访问每个边缘
|
||||
* [哈密顿图](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/hamiltonian-cycle) - 恰好访问每个顶点一次
|
||||
* [强连通分量](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/strongly-connected-components) - Kosaraju算法
|
||||
* [旅行推销员问题](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/travelling-salesman) - 尽可能以最短的路线访问每个城市并返回原始城市
|
||||
* **未分类**
|
||||
* [汉诺塔](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/uncategorized/hanoi-tower)
|
||||
* [八皇后问题](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/uncategorized/n-queens)
|
||||
* [骑士巡逻](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/uncategorized/knight-tour)
|
||||
|
||||
### 算法范式
|
||||
|
||||
算法范式是基于类的设计的通用方法或方法的算法。 这是一个比算法概念更高的抽象,就像一个
|
||||
算法是比计算机程序更高的抽象。
|
||||
|
||||
* **BF算法** - 查找所有可能性并选择最佳解决方案
|
||||
* [最大子数列](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/maximum-subarray)
|
||||
* [旅行推销员问题](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/travelling-salesman) - 尽可能以最短的路线访问每个城市并返回原始城市
|
||||
|
||||
* **贪心法** - 在当前选择最佳选项,不考虑以后情况
|
||||
* [背包问题](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/knapsack-problem)
|
||||
* [戴克斯特拉算法](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/dijkstra) - 找到所有图顶点的最短路径
|
||||
* [普里姆算法](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/prim) - 寻找加权无向图的最小生成树(MST)
|
||||
* [克鲁斯卡尔算法](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/kruskal) - 寻找加权无向图的最小生成树(MST)
|
||||
* **分治法** - 将问题分成较小的部分,然后解决这些部分
|
||||
* [二分查找](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/search/binary-search)
|
||||
* [汉诺塔](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/uncategorized/hanoi-tower)
|
||||
* [欧几里得算法](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/euclidean-algorithm) - 计算最大公约数(GCD)
|
||||
* [排列](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/permutations) (有/无重复)
|
||||
* [组合](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/combinations) (有/无重复)
|
||||
* [归并排序](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sorting/merge-sort)
|
||||
* [Quicksort](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sorting/quick-sort)
|
||||
* [树深度优先搜索](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/tree/depth-first-search) (DFS)
|
||||
* [图深度优先搜索](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/depth-first-search) (DFS)
|
||||
* **动态编程** - 使用以前找到的子解决方案构建解决方案
|
||||
* [斐波那契数](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/fibonacci)
|
||||
* [莱温斯坦距离](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/string/levenshtein-distance) - 两个序列之间的最小编辑距离
|
||||
* [最长公共子序列](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/longest-common-subsequnce) (LCS)
|
||||
* [最长公共子串](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/string/longest-common-substring)
|
||||
* [最长递增子序列](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/longest-increasing-subsequence)
|
||||
* [最短公共子序列](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/shortest-common-supersequence)
|
||||
* [0-1背包问题](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/knapsack-problem)
|
||||
* [整数拆分](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/integer-partition)
|
||||
* [最大子数列](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/maximum-subarray)
|
||||
* [贝尔曼-福特算法](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/bellman-ford) - 找到所有图顶点的最短路径
|
||||
* **回溯法** - 类似于 BF算法 试图产生所有可能的解决方案,但每次生成解决方案测试如果它满足所有条件,那么只有继续生成后续解决方案。 否则回溯并继续寻找不同路径的解决方案。
|
||||
* [哈密顿图](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/hamiltonian-cycle) - 恰好访问每个顶点一次
|
||||
* [八皇后问题](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/uncategorized/n-queens)
|
||||
* [骑士巡逻](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/uncategorized/knight-tour)
|
||||
* **B & B**
|
||||
|
||||
## 如何使用本仓库
|
||||
|
||||
**安装依赖**
|
||||
```
|
||||
npm install
|
||||
```
|
||||
|
||||
**执行测试**
|
||||
```
|
||||
npm test
|
||||
```
|
||||
|
||||
**按照名称执行测试**
|
||||
```
|
||||
npm test -- -t 'LinkedList'
|
||||
```
|
||||
|
||||
**Playground**
|
||||
|
||||
你可以在`./src/playground/playground.js`文件中操作数据结构与算法,并在`./src/playground/__test__/playground.test.js`中编写测试。
|
||||
|
||||
然后,只需运行以下命令来测试你的 Playground 是否按无误:
|
||||
|
||||
```
|
||||
npm test -- -t 'playground'
|
||||
```
|
||||
|
||||
## 有用的信息
|
||||
|
||||
### 引用
|
||||
|
||||
[▶ YouTube](https://www.youtube.com/playlist?list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
|
||||
|
||||
### 大O符号
|
||||
|
||||
大O符号中指定的算法的增长顺序。
|
||||
|
||||
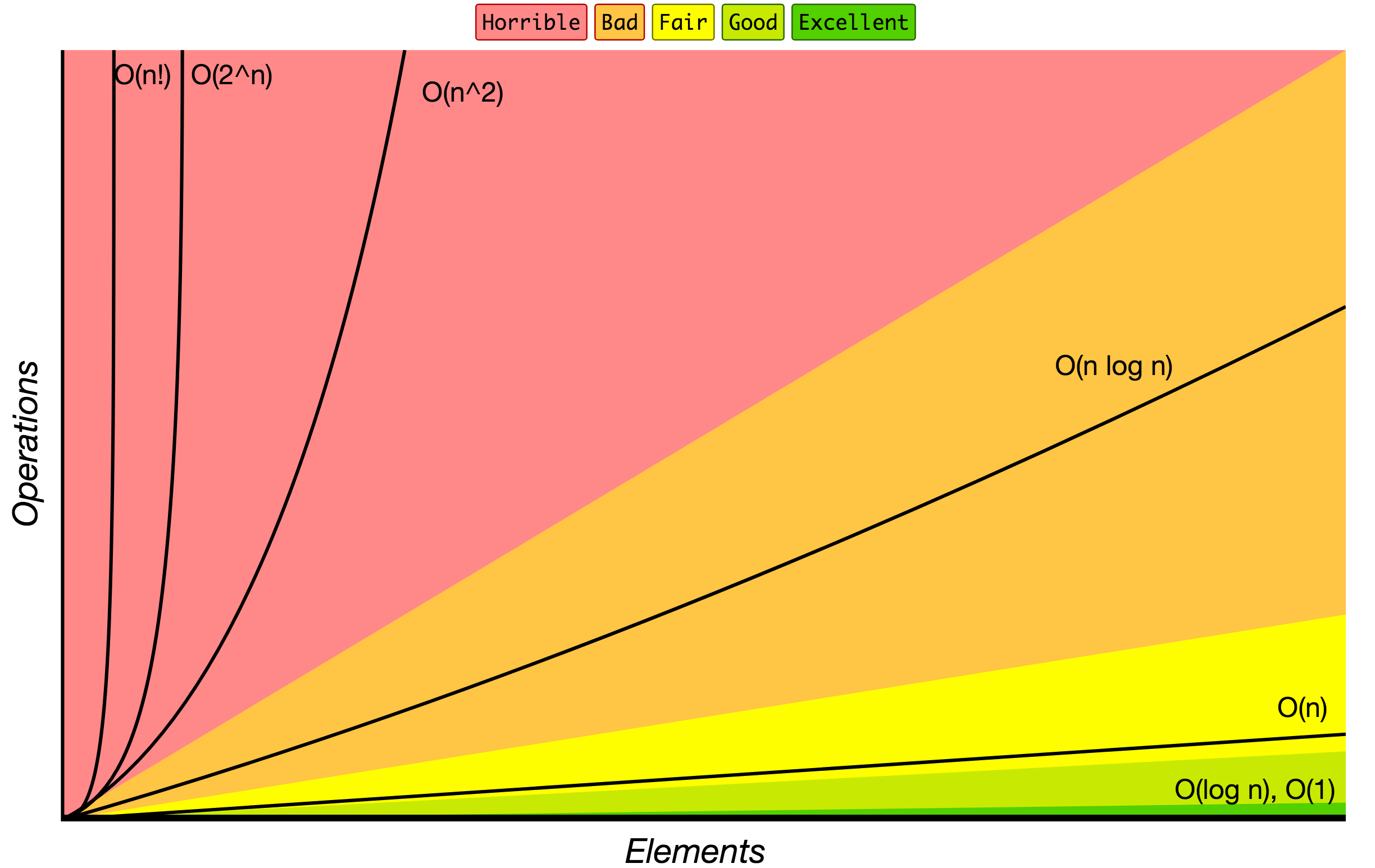
|
||||
|
||||
源: [Big O Cheat Sheet](http://bigocheatsheet.com/).
|
||||
|
||||
以下是一些最常用的 大O标记法 列表以及它们与不同大小输入数据的性能比较。
|
||||
|
||||
| 大O标记法 | 计算10个元素 | 计算100个元素 | 计算1000个元素 |
|
||||
| -------------- | ---------------------------- | ----------------------------- | ------------------------------- |
|
||||
| **O(1)** | 1 | 1 | 1 |
|
||||
| **O(log N)** | 3 | 6 | 9 |
|
||||
| **O(N)** | 10 | 100 | 1000 |
|
||||
| **O(N log N)** | 30 | 60 | 9000 |
|
||||
| **O(N^2)** | 100 | 10000 | 1000000 |
|
||||
| **O(2^N)** | 1024 | 1.26e+29 | 1.07e+301 |
|
||||
| **O(N!)** | 3628800 | 9.3e+157 | 4.02e+2567 |
|
||||
|
||||
### 数据结构操作的复杂性
|
||||
|
||||
| 数据结构 | 连接 | 查找 | 插入 | 删除 |
|
||||
| ----------------------- | :-------: | :-------: | :-------: | :-------: |
|
||||
| **数组** | 1 | n | n | n |
|
||||
| **栈** | n | n | 1 | 1 |
|
||||
| **队列** | n | n | 1 | 1 |
|
||||
| **链表** | n | n | 1 | 1 |
|
||||
| **哈希表** | - | n | n | n |
|
||||
| **二分查找树** | n | n | n | n |
|
||||
| **B树** | log(n) | log(n) | log(n) | log(n) |
|
||||
| **红黑树** | log(n) | log(n) | log(n) | log(n) |
|
||||
| **AVL树** | log(n) | log(n) | log(n) | log(n) |
|
||||
|
||||
### 数组排序算法的复杂性
|
||||
|
||||
| 名称 | 最优 | 平均 | 最坏 | 内存 | 稳定 |
|
||||
| --------------------- | :-------: | :-------: | :-----------: | :-------: | :-------: |
|
||||
| **冒泡排序** | n | n^2 | n^2 | 1 | Yes |
|
||||
| **插入排序** | n | n^2 | n^2 | 1 | Yes |
|
||||
| **选择排序** | n^2 | n^2 | n^2 | 1 | No |
|
||||
| **堆排序** | n log(n) | n log(n) | n log(n) | 1 | No |
|
||||
| **归并排序** | n log(n) | n log(n) | n log(n) | n | Yes |
|
||||
| **快速排序** | n log(n) | n log(n) | n^2 | log(n) | No |
|
||||
| **希尔排序** | n log(n) | 取决于差距序列 | n (log(n))^2 | 1 | No |
|
||||
@ -22,7 +22,7 @@ export default function binarySearch(sortedArray, seekElement, comparatorCallbac
|
||||
}
|
||||
|
||||
// Decide which half to choose for seeking next: left or right one.
|
||||
if (comparator.lessThen(sortedArray[middleIndex], seekElement)) {
|
||||
if (comparator.lessThan(sortedArray[middleIndex], seekElement)) {
|
||||
// Go to the right half of the array.
|
||||
startIndex = middleIndex + 1;
|
||||
} else {
|
||||
|
||||
@ -18,7 +18,7 @@ export default class BubbleSort extends Sort {
|
||||
this.callbacks.visitingCallback(array[j]);
|
||||
|
||||
// Swap elements if they are in wrong order.
|
||||
if (this.comparator.lessThen(array[j + 1], array[j])) {
|
||||
if (this.comparator.lessThan(array[j + 1], array[j])) {
|
||||
const tmp = array[j + 1];
|
||||
array[j + 1] = array[j];
|
||||
array[j] = tmp;
|
||||
|
||||
@ -15,7 +15,7 @@ export default class InsertionSort extends Sort {
|
||||
// If this is the case then swap that elements.
|
||||
while (
|
||||
array[currentIndex - 1] &&
|
||||
this.comparator.lessThen(array[currentIndex], array[currentIndex - 1])
|
||||
this.comparator.lessThan(array[currentIndex], array[currentIndex - 1])
|
||||
) {
|
||||
// Call visiting callback.
|
||||
this.callbacks.visitingCallback(array[currentIndex - 1]);
|
||||
|
||||
@ -31,7 +31,7 @@ export default class MergeSort extends Sort {
|
||||
let minimumElement = null;
|
||||
|
||||
// Find minimum element of two arrays.
|
||||
if (this.comparator.lessThenOrEqual(leftArray[0], rightArray[0])) {
|
||||
if (this.comparator.lessThanOrEqual(leftArray[0], rightArray[0])) {
|
||||
minimumElement = leftArray.shift();
|
||||
} else {
|
||||
minimumElement = rightArray.shift();
|
||||
|
||||
@ -27,7 +27,7 @@ export default class QuickSort extends Sort {
|
||||
|
||||
if (this.comparator.equal(currentElement, pivotElement)) {
|
||||
centerArray.push(currentElement);
|
||||
} else if (this.comparator.lessThen(currentElement, pivotElement)) {
|
||||
} else if (this.comparator.lessThan(currentElement, pivotElement)) {
|
||||
leftArray.push(currentElement);
|
||||
} else {
|
||||
rightArray.push(currentElement);
|
||||
|
||||
@ -16,7 +16,7 @@ export default class SelectionSort extends Sort {
|
||||
// Call visiting callback.
|
||||
this.callbacks.visitingCallback(array[j]);
|
||||
|
||||
if (this.comparator.lessThen(array[j], array[minIndex])) {
|
||||
if (this.comparator.lessThan(array[j], array[minIndex])) {
|
||||
minIndex = j;
|
||||
}
|
||||
}
|
||||
|
||||
@ -20,7 +20,7 @@ export default class ShellSort extends Sort {
|
||||
this.callbacks.visitingCallback(array[currentIndex]);
|
||||
|
||||
// Compare and swap array elements if needed.
|
||||
if (this.comparator.lessThen(array[gapShiftedIndex], array[currentIndex])) {
|
||||
if (this.comparator.lessThan(array[gapShiftedIndex], array[currentIndex])) {
|
||||
const tmp = array[currentIndex];
|
||||
array[currentIndex] = array[gapShiftedIndex];
|
||||
array[gapShiftedIndex] = tmp;
|
||||
|
||||
@ -4,7 +4,7 @@
|
||||
* @return {number[][]}
|
||||
*/
|
||||
function getPossibleMoves(chessboard, position) {
|
||||
// Generate all knight moves (event those that goes beyond the board).
|
||||
// Generate all knight moves (even those that go beyond the board).
|
||||
const possibleMoves = [
|
||||
[position[0] - 1, position[1] - 2],
|
||||
[position[0] - 2, position[1] - 1],
|
||||
|
||||
@ -167,7 +167,7 @@ export default class MinHeap {
|
||||
leftChild !== null &&
|
||||
(
|
||||
parentItem === null ||
|
||||
this.compare.lessThen(parentItem, this.heapContainer[indexToRemove])
|
||||
this.compare.lessThan(parentItem, this.heapContainer[indexToRemove])
|
||||
)
|
||||
) {
|
||||
this.heapifyDown(indexToRemove);
|
||||
@ -209,7 +209,7 @@ export default class MinHeap {
|
||||
|
||||
while (
|
||||
this.hasParent(currentIndex) &&
|
||||
this.compare.lessThen(this.heapContainer[currentIndex], this.parent(currentIndex))
|
||||
this.compare.lessThan(this.heapContainer[currentIndex], this.parent(currentIndex))
|
||||
) {
|
||||
this.swap(currentIndex, this.getParentIndex(currentIndex));
|
||||
currentIndex = this.getParentIndex(currentIndex);
|
||||
@ -228,14 +228,14 @@ export default class MinHeap {
|
||||
while (this.hasLeftChild(currentIndex)) {
|
||||
if (
|
||||
this.hasRightChild(currentIndex) &&
|
||||
this.compare.lessThen(this.rightChild(currentIndex), this.leftChild(currentIndex))
|
||||
this.compare.lessThan(this.rightChild(currentIndex), this.leftChild(currentIndex))
|
||||
) {
|
||||
nextIndex = this.getRightChildIndex(currentIndex);
|
||||
} else {
|
||||
nextIndex = this.getLeftChildIndex(currentIndex);
|
||||
}
|
||||
|
||||
if (this.compare.lessThen(this.heapContainer[currentIndex], this.heapContainer[nextIndex])) {
|
||||
if (this.compare.lessThan(this.heapContainer[currentIndex], this.heapContainer[nextIndex])) {
|
||||
break;
|
||||
}
|
||||
|
||||
|
||||
@ -23,20 +23,20 @@ export default class Comparator {
|
||||
return this.compare(a, b) === 0;
|
||||
}
|
||||
|
||||
lessThen(a, b) {
|
||||
lessThan(a, b) {
|
||||
return this.compare(a, b) < 0;
|
||||
}
|
||||
|
||||
greaterThen(a, b) {
|
||||
greaterThan(a, b) {
|
||||
return this.compare(a, b) > 0;
|
||||
}
|
||||
|
||||
lessThenOrEqual(a, b) {
|
||||
return this.lessThen(a, b) || this.equal(a, b);
|
||||
lessThanOrEqual(a, b) {
|
||||
return this.lessThan(a, b) || this.equal(a, b);
|
||||
}
|
||||
|
||||
greaterThenOrEqual(a, b) {
|
||||
return this.greaterThen(a, b) || this.equal(a, b);
|
||||
greaterThanOrEqual(a, b) {
|
||||
return this.greaterThan(a, b) || this.equal(a, b);
|
||||
}
|
||||
|
||||
reverse() {
|
||||
|
||||
@ -7,19 +7,19 @@ describe('Comparator', () => {
|
||||
expect(comparator.equal(0, 0)).toBeTruthy();
|
||||
expect(comparator.equal(0, 1)).toBeFalsy();
|
||||
expect(comparator.equal('a', 'a')).toBeTruthy();
|
||||
expect(comparator.lessThen(1, 2)).toBeTruthy();
|
||||
expect(comparator.lessThen(-1, 2)).toBeTruthy();
|
||||
expect(comparator.lessThen('a', 'b')).toBeTruthy();
|
||||
expect(comparator.lessThen('a', 'ab')).toBeTruthy();
|
||||
expect(comparator.lessThen(10, 2)).toBeFalsy();
|
||||
expect(comparator.lessThenOrEqual(10, 2)).toBeFalsy();
|
||||
expect(comparator.lessThenOrEqual(1, 1)).toBeTruthy();
|
||||
expect(comparator.lessThenOrEqual(0, 0)).toBeTruthy();
|
||||
expect(comparator.greaterThen(0, 0)).toBeFalsy();
|
||||
expect(comparator.greaterThen(10, 0)).toBeTruthy();
|
||||
expect(comparator.greaterThenOrEqual(10, 0)).toBeTruthy();
|
||||
expect(comparator.greaterThenOrEqual(10, 10)).toBeTruthy();
|
||||
expect(comparator.greaterThenOrEqual(0, 10)).toBeFalsy();
|
||||
expect(comparator.lessThan(1, 2)).toBeTruthy();
|
||||
expect(comparator.lessThan(-1, 2)).toBeTruthy();
|
||||
expect(comparator.lessThan('a', 'b')).toBeTruthy();
|
||||
expect(comparator.lessThan('a', 'ab')).toBeTruthy();
|
||||
expect(comparator.lessThan(10, 2)).toBeFalsy();
|
||||
expect(comparator.lessThanOrEqual(10, 2)).toBeFalsy();
|
||||
expect(comparator.lessThanOrEqual(1, 1)).toBeTruthy();
|
||||
expect(comparator.lessThanOrEqual(0, 0)).toBeTruthy();
|
||||
expect(comparator.greaterThan(0, 0)).toBeFalsy();
|
||||
expect(comparator.greaterThan(10, 0)).toBeTruthy();
|
||||
expect(comparator.greaterThanOrEqual(10, 0)).toBeTruthy();
|
||||
expect(comparator.greaterThanOrEqual(10, 10)).toBeTruthy();
|
||||
expect(comparator.greaterThanOrEqual(0, 10)).toBeFalsy();
|
||||
});
|
||||
|
||||
it('should compare with custom comparator function', () => {
|
||||
@ -33,18 +33,18 @@ describe('Comparator', () => {
|
||||
|
||||
expect(comparator.equal('a', 'b')).toBeTruthy();
|
||||
expect(comparator.equal('a', '')).toBeFalsy();
|
||||
expect(comparator.lessThen('b', 'aa')).toBeTruthy();
|
||||
expect(comparator.greaterThenOrEqual('a', 'aa')).toBeFalsy();
|
||||
expect(comparator.greaterThenOrEqual('aa', 'a')).toBeTruthy();
|
||||
expect(comparator.greaterThenOrEqual('a', 'a')).toBeTruthy();
|
||||
expect(comparator.lessThan('b', 'aa')).toBeTruthy();
|
||||
expect(comparator.greaterThanOrEqual('a', 'aa')).toBeFalsy();
|
||||
expect(comparator.greaterThanOrEqual('aa', 'a')).toBeTruthy();
|
||||
expect(comparator.greaterThanOrEqual('a', 'a')).toBeTruthy();
|
||||
|
||||
comparator.reverse();
|
||||
|
||||
expect(comparator.equal('a', 'b')).toBeTruthy();
|
||||
expect(comparator.equal('a', '')).toBeFalsy();
|
||||
expect(comparator.lessThen('b', 'aa')).toBeFalsy();
|
||||
expect(comparator.greaterThenOrEqual('a', 'aa')).toBeTruthy();
|
||||
expect(comparator.greaterThenOrEqual('aa', 'a')).toBeFalsy();
|
||||
expect(comparator.greaterThenOrEqual('a', 'a')).toBeTruthy();
|
||||
expect(comparator.lessThan('b', 'aa')).toBeFalsy();
|
||||
expect(comparator.greaterThanOrEqual('a', 'aa')).toBeTruthy();
|
||||
expect(comparator.greaterThanOrEqual('aa', 'a')).toBeFalsy();
|
||||
expect(comparator.greaterThanOrEqual('a', 'a')).toBeTruthy();
|
||||
});
|
||||
});
|
||||
|
||||
Loading…
Reference in New Issue
Block a user