mirror of
https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git
synced 2024-12-26 07:01:18 +08:00
Implement Discrete Fourier Transform function.
This commit is contained in:
parent
53a0b6168d
commit
12d649e372
@ -73,6 +73,7 @@ a set of rules that precisely define a sequence of operations.
|
||||
* `B` [Radian & Degree](src/algorithms/math/radian) - radians to degree and backwards conversion
|
||||
* `A` [Integer Partition](src/algorithms/math/integer-partition)
|
||||
* `A` [Liu Hui π Algorithm](src/algorithms/math/liu-hui) - approximate π calculations based on N-gons
|
||||
* `A` [Fourier Transform (DFT, FFT)](src/algorithms/math/fourier-transform) - decompose a function of time (a signal) into the frequencies that make it up
|
||||
* **Sets**
|
||||
* `B` [Cartesian Product](src/algorithms/sets/cartesian-product) - product of multiple sets
|
||||
* `B` [Fisher–Yates Shuffle](src/algorithms/sets/fisher-yates) - random permutation of a finite sequence
|
||||
|
||||
@ -78,12 +78,49 @@ Rather than jumping into the symbols, let's experience the key idea firsthand. H
|
||||
- *Why?* Recipes are easier to analyze, compare, and modify than the smoothie itself.
|
||||
- *How do we get the smoothie back?* Blend the ingredients.
|
||||
|
||||
**Think With Circles, Not Just Sinusoids**
|
||||
|
||||
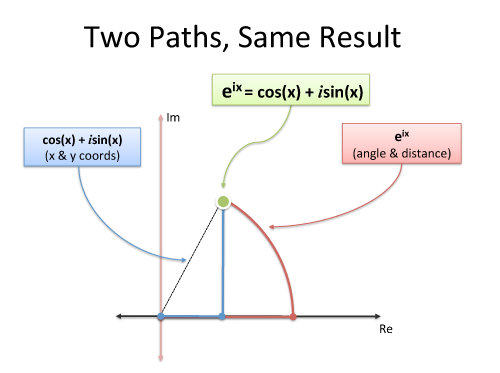
The Fourier Transform is about circular paths (not 1-d sinusoids) and Euler's
|
||||
formula is a clever way to generate one:
|
||||
|
||||
|
||||
|
||||
Must we use imaginary exponents to move in a circle? Nope. But it's convenient
|
||||
and compact. And sure, we can describe our path as coordinated motion in two
|
||||
dimensions (real and imaginary), but don't forget the big picture: we're just
|
||||
moving in a circle.
|
||||
|
||||
**Discovering The Full Transform**
|
||||
|
||||
The big insight: our signal is just a bunch of time spikes! If we merge the
|
||||
recipes for each time spike, we should get the recipe for the full signal.
|
||||
|
||||
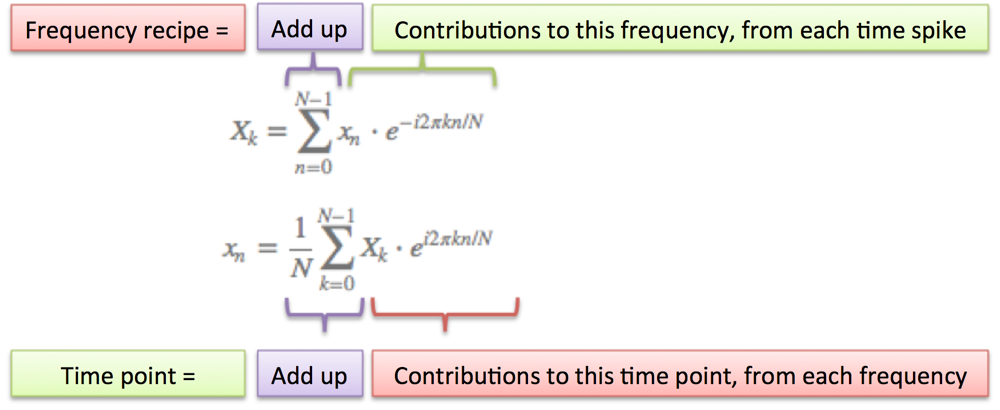
The Fourier Transform builds the recipe frequency-by-frequency:
|
||||
|
||||
|
||||
|
||||
A few notes:
|
||||
|
||||
- N = number of time samples we have
|
||||
- n = current sample we're considering (0 ... N-1)
|
||||
- x<sub>n</sub> = value of the signal at time n
|
||||
- k = current frequency we're considering (0 Hertz up to N-1 Hertz)
|
||||
- X<sub>k</sub> = amount of frequency k in the signal (amplitude and phase, a complex number)
|
||||
- The 1/N factor is usually moved to the reverse transform (going from frequencies back to time). This is allowed, though I prefer 1/N in the forward transform since it gives the actual sizes for the time spikes. You can get wild and even use 1/sqrt(N) on both transforms (going forward and back creates the 1/N factor).
|
||||
- n/N is the percent of the time we've gone through. 2 * pi * k is our speed in radians / sec. e^-ix is our backwards-moving circular path. The combination is how far we've moved, for this speed and time.
|
||||
- The raw equations for the Fourier Transform just say "add the complex numbers". Many programming languages cannot handle complex numbers directly, so you convert everything to rectangular coordinates and add those.
|
||||
|
||||
Stuart Riffle has a great interpretation of the Fourier Transform:
|
||||
|
||||
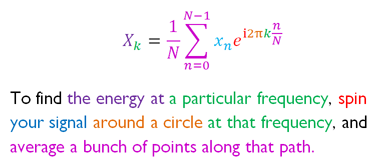
|
||||
|
||||
## References
|
||||
|
||||
- [An Interactive Guide To The Fourier Transform](https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/)
|
||||
- [YouTube by Better Explained](https://www.youtube.com/watch?v=iN0VG9N2q0U&t=0s&index=77&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
|
||||
- [YouTube by 3Blue1Brown](https://www.youtube.com/watch?v=spUNpyF58BY&t=0s&index=76&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
|
||||
- [Wikipedia, FT](https://en.wikipedia.org/wiki/Fourier_transform)
|
||||
- [Wikipedia, DFT](https://www.wikiwand.com/en/Discrete_Fourier_transform)
|
||||
- [Wikipedia, DTFT](https://en.wikipedia.org/wiki/Discrete-time_Fourier_transform)
|
||||
- [Wikipedia, FFT](https://www.wikiwand.com/en/Fast_Fourier_transform)
|
||||
- Wikipedia
|
||||
- [FT](https://en.wikipedia.org/wiki/Fourier_transform)
|
||||
- [DFT](https://www.wikiwand.com/en/Discrete_Fourier_transform)
|
||||
- [DTFT](https://en.wikipedia.org/wiki/Discrete-time_Fourier_transform)
|
||||
- [FFT](https://www.wikiwand.com/en/Fast_Fourier_transform)
|
||||
|
||||
@ -1,9 +1,143 @@
|
||||
import discreteFourierTransform from '../discreteFourierTransform';
|
||||
|
||||
describe('discreteFourierTransform', () => {
|
||||
it('should calculate split signal into frequencies', () => {
|
||||
const frequencies = discreteFourierTransform([1, 0, 0, 0]);
|
||||
/**
|
||||
* Helper class of the output Signal.
|
||||
*/
|
||||
class Sgnl {
|
||||
constructor(frequency, amplitude, phase) {
|
||||
this.frequency = frequency;
|
||||
this.amplitude = amplitude;
|
||||
this.phase = phase;
|
||||
}
|
||||
}
|
||||
|
||||
expect(frequencies).toBeDefined();
|
||||
describe('discreteFourierTransform', () => {
|
||||
it('should split signal into frequencies', () => {
|
||||
const testCases = [
|
||||
{
|
||||
inputAmplitudes: [1],
|
||||
outputSignals: [
|
||||
new Sgnl(0, 1, 0),
|
||||
],
|
||||
},
|
||||
{
|
||||
inputAmplitudes: [1, 0],
|
||||
outputSignals: [
|
||||
new Sgnl(0, 0.5, 0),
|
||||
new Sgnl(1, 0.5, 0),
|
||||
],
|
||||
},
|
||||
{
|
||||
inputAmplitudes: [2, 0],
|
||||
outputSignals: [
|
||||
new Sgnl(0, 1, 0),
|
||||
new Sgnl(1, 1, 0),
|
||||
],
|
||||
},
|
||||
{
|
||||
inputAmplitudes: [1, 0, 0],
|
||||
outputSignals: [
|
||||
new Sgnl(0, 0.33, 0),
|
||||
new Sgnl(1, 0.33, 0),
|
||||
new Sgnl(2, 0.33, 0),
|
||||
],
|
||||
},
|
||||
{
|
||||
inputAmplitudes: [1, 0, 0, 0],
|
||||
outputSignals: [
|
||||
new Sgnl(0, 0.25, 0),
|
||||
new Sgnl(1, 0.25, 0),
|
||||
new Sgnl(2, 0.25, 0),
|
||||
new Sgnl(3, 0.25, 0),
|
||||
],
|
||||
},
|
||||
{
|
||||
inputAmplitudes: [0, 1, 0, 0],
|
||||
outputSignals: [
|
||||
new Sgnl(0, 0.25, 0),
|
||||
new Sgnl(1, 0.25, -90),
|
||||
new Sgnl(2, 0.25, 180),
|
||||
new Sgnl(3, 0.25, 90),
|
||||
],
|
||||
},
|
||||
{
|
||||
inputAmplitudes: [0, 0, 1, 0],
|
||||
outputSignals: [
|
||||
new Sgnl(0, 0.25, 0),
|
||||
new Sgnl(1, 0.25, 180),
|
||||
new Sgnl(2, 0.25, 0),
|
||||
new Sgnl(3, 0.25, 180),
|
||||
],
|
||||
},
|
||||
{
|
||||
inputAmplitudes: [0, 0, 0, 2],
|
||||
outputSignals: [
|
||||
new Sgnl(0, 0.5, 0),
|
||||
new Sgnl(1, 0.5, 90),
|
||||
new Sgnl(2, 0.5, 180),
|
||||
new Sgnl(3, 0.5, -90),
|
||||
],
|
||||
},
|
||||
{
|
||||
inputAmplitudes: [0, 1, 0, 2],
|
||||
outputSignals: [
|
||||
new Sgnl(0, 0.75, 0),
|
||||
new Sgnl(1, 0.25, 90),
|
||||
new Sgnl(2, 0.75, 180),
|
||||
new Sgnl(3, 0.25, -90),
|
||||
],
|
||||
},
|
||||
{
|
||||
inputAmplitudes: [4, 1, 0, 2],
|
||||
outputSignals: [
|
||||
new Sgnl(0, 1.75, 0),
|
||||
new Sgnl(1, 1.03, 14),
|
||||
new Sgnl(2, 0.25, 0),
|
||||
new Sgnl(3, 1.03, -14),
|
||||
],
|
||||
},
|
||||
{
|
||||
inputAmplitudes: [4, 1, -3, 2],
|
||||
outputSignals: [
|
||||
new Sgnl(0, 1, 0),
|
||||
new Sgnl(1, 1.77, 8),
|
||||
new Sgnl(2, 0.5, 180),
|
||||
new Sgnl(3, 1.77, -8),
|
||||
],
|
||||
},
|
||||
{
|
||||
inputAmplitudes: [1, 2, 3, 4],
|
||||
outputSignals: [
|
||||
new Sgnl(0, 2.5, 0),
|
||||
new Sgnl(1, 0.71, 135),
|
||||
new Sgnl(2, 0.5, 180),
|
||||
new Sgnl(3, 0.71, -135),
|
||||
],
|
||||
},
|
||||
];
|
||||
|
||||
testCases.forEach((testCase) => {
|
||||
const { inputAmplitudes, outputSignals } = testCase;
|
||||
|
||||
// Try to split input signal into sequence of pure sinusoids.
|
||||
const signals = discreteFourierTransform(inputAmplitudes);
|
||||
|
||||
// Check the signal has been split into proper amount of sub-signals.
|
||||
expect(signals.length).toBe(outputSignals.length);
|
||||
|
||||
// Now go through all the signals and check their frequency, amplitude and phase.
|
||||
signals.forEach((signal, frequency) => {
|
||||
// Get polar form of calculated sub-signal since it is more convenient to analyze.
|
||||
const signalPolarForm = signal.getPolarForm(false);
|
||||
|
||||
// Get template data we want to test against.
|
||||
const signalTemplate = outputSignals[frequency];
|
||||
|
||||
// Check all signal parameters.
|
||||
expect(frequency).toBe(signalTemplate.frequency);
|
||||
expect(signalPolarForm.radius).toBeCloseTo(signalTemplate.amplitude, 2);
|
||||
expect(signalPolarForm.phase).toBeCloseTo(signalTemplate.phase, 0);
|
||||
});
|
||||
});
|
||||
});
|
||||
});
|
||||
|
||||
@ -1,55 +1,55 @@
|
||||
import ComplexNumber from '../complex-number/ComplexNumber';
|
||||
|
||||
/**
|
||||
* @param {number[]} data
|
||||
* @return {*[]}
|
||||
* @param {number[]} inputSignalAmplitudes - Input signal amplitudes over time (i.e. [1, 0, 4]).
|
||||
* @return {ComplexNumber[]} - Array of complex number. Each of the number represents the frequency
|
||||
* or signal. All signals together will form input signal over discrete time periods. Each signal's
|
||||
* complex number has radius (amplitude) and phase (angle) in polar form that describes the signal.
|
||||
*
|
||||
* @see https://gist.github.com/anonymous/129d477ddb1c8025c9ac
|
||||
* @see https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/
|
||||
*/
|
||||
export default function discreteFourierTransform(data) {
|
||||
const N = data.length;
|
||||
const frequencies = [];
|
||||
export default function discreteFourierTransform(inputSignalAmplitudes) {
|
||||
const N = inputSignalAmplitudes.length;
|
||||
const outpuFrequencies = [];
|
||||
|
||||
// for every frequency...
|
||||
for (let frequency = 0; frequency < N; frequency += 1) {
|
||||
let re = 0;
|
||||
let im = 0;
|
||||
// For every frequency discrete...
|
||||
for (let frequencyValue = 0; frequencyValue < N; frequencyValue += 1) {
|
||||
let signal = new ComplexNumber();
|
||||
|
||||
// for every point in time...
|
||||
// For every discrete point in time...
|
||||
for (let t = 0; t < N; t += 1) {
|
||||
// Spin the signal _backwards_ at each frequency (as radians/s, not Hertz)
|
||||
const rate = -1 * (2 * Math.PI) * frequency;
|
||||
const rate = -1 * (2 * Math.PI) * frequencyValue;
|
||||
|
||||
// How far around the circle have we gone at time=t?
|
||||
const time = t / N;
|
||||
const distance = rate * time;
|
||||
|
||||
// Data-point * e^(-i*2*pi*f) is complex, store each part.
|
||||
const rePart = data[t] * Math.cos(distance);
|
||||
const imPart = data[t] * Math.sin(distance);
|
||||
const dataPointContribution = new ComplexNumber({
|
||||
re: inputSignalAmplitudes[t] * Math.cos(distance),
|
||||
im: inputSignalAmplitudes[t] * Math.sin(distance),
|
||||
});
|
||||
|
||||
// add this data point's contribution
|
||||
re += rePart;
|
||||
im += imPart;
|
||||
// Add this data point's contribution.
|
||||
signal = signal.add(dataPointContribution);
|
||||
}
|
||||
|
||||
// Close to zero? You're zero.
|
||||
if (Math.abs(re) < 1e-10) {
|
||||
re = 0;
|
||||
if (Math.abs(signal.re) < 1e-10) {
|
||||
signal.re = 0;
|
||||
}
|
||||
|
||||
if (Math.abs(im) < 1e-10) {
|
||||
im = 0;
|
||||
if (Math.abs(signal.im) < 1e-10) {
|
||||
signal.im = 0;
|
||||
}
|
||||
|
||||
// Average contribution at this frequency
|
||||
re /= N;
|
||||
im /= N;
|
||||
signal = signal.divide(N);
|
||||
|
||||
frequencies[frequency] = {
|
||||
re,
|
||||
im,
|
||||
frequency,
|
||||
amp: Math.sqrt((re ** 2) + (im ** 2)),
|
||||
phase: Math.atan2(im, re) * 180 / Math.PI, // in degrees
|
||||
};
|
||||
outpuFrequencies[frequencyValue] = signal;
|
||||
}
|
||||
|
||||
return frequencies;
|
||||
return outpuFrequencies;
|
||||
}
|
||||
|
||||
Loading…
Reference in New Issue
Block a user