Add red-black tree.

2024-11-10 11:09:43 +08:00 · 2018-06-02 08:15:40 +03:00 · 2018-06-02 08:15:40 +03:00 · 19789c6a94
commit 19789c6a94
parent 48f7ea1ad5
4 changed files with 697 additions and 1 deletions
--- a/README.md
+++ b/README.md
@ -31,7 +31,7 @@ the data.
 * [Tree](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/tree)
    * [Binary Search Tree](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/tree/binary-search-tree)
    * [AVL Tree](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/tree/avl-tree)
-    * Red-Black Tree
+    * [Red-Black Tree](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/tree/red-black-tree)
    * Suffix Tree
    * Segment Tree or Interval Tree
    * Binary Indexed Tree or Fenwick Tree
--- a/src/data-structures/tree/red-black-tree/README.md
+++ b/src/data-structures/tree/red-black-tree/README.md
@ -0,0 +1,93 @@
+# Red–Black Tree
+
+A red–black tree is a kind of self-balancing binary search 
+tree in computer science. Each node of the binary tree has 
+an extra bit, and that bit is often interpreted as the 
+color (red or black) of the node. These color bits are used 
+to ensure the tree remains approximately balanced during 
+insertions and deletions.
+
+Balance is preserved by painting each node of the tree with 
+one of two colors in a way that satisfies certain properties,
+which collectively constrain how unbalanced the tree can 
+become in the worst case. When the tree is modified, the 
+new tree is subsequently rearranged and repainted to 
+restore the coloring properties. The properties are 
+designed in such a way that this rearranging and recoloring 
+can be performed efficiently.
+
+The balancing of the tree is not perfect, but it is good 
+enough to allow it to guarantee searching in `O(log n)` time,
+where `n` is the total number of elements in the tree. 
+The insertion and deletion operations, along with the tree 
+rearrangement and recoloring, are also performed 
+in `O(log n)` time.
+
+An example of a red–black tree:
+
+![red-black tree](https://upload.wikimedia.org/wikipedia/commons/6/66/Red-black_tree_example.svg)
+
+## Properties
+
+In addition to the requirements imposed on a binary search 
+tree the following must be satisfied by a red–black tree:
+
+- Each node is either red or black.
+- The root is black. This rule is sometimes omitted. 
+Since the root can always be changed from red to black, 
+but not necessarily vice versa, this rule has little 
+effect on analysis.
+- All leaves (NIL) are black.
+- If a node is red, then both its children are black.
+- Every path from a given node to any of its descendant 
+NIL nodes contains the same number of black nodes.
+
+Some definitions: the number of black nodes from the root 
+to a node is the node's **black depth**; the uniform 
+number of black nodes in all paths from root to the leaves 
+is called the **black-height** of the red–black tree.
+
+These constraints enforce a critical property of red–black 
+trees: _the path from the root to the farthest leaf is no more than twice as long as the path from the root to the nearest leaf_. 
+The result is that the tree is roughly height-balanced. 
+Since operations such as inserting, deleting, and finding 
+values require worst-case time proportional to the height 
+of the tree, this theoretical upper bound on the height 
+allows red–black trees to be efficient in the worst case, 
+unlike ordinary binary search trees.
+
+## Balancing during insertion
+
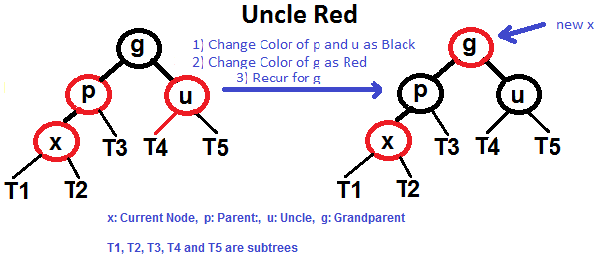
+### If uncle is RED
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase2.png)
+
+### If uncle is BLACK
+
+- Left Left Case (`p` is left child of `g` and `x` is left child of `p`)
+- Left Right Case (`p` is left child of `g` and `x` is right child of `p`)
+- Right Right Case (`p` is right child of `g` and `x` is right child of `p`)
+- Right Left Case (`p` is right child of `g` and `x` is left child of `p`)
+
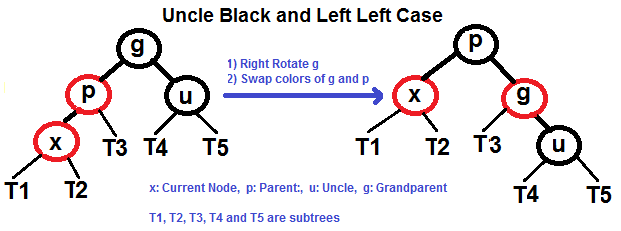
+#### Left Left Case (See g, p and x)
+
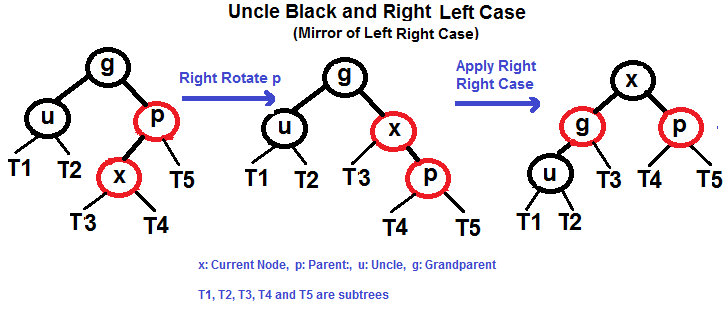
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3a1.png)
+
+#### Left Right Case (See g, p and x)
+
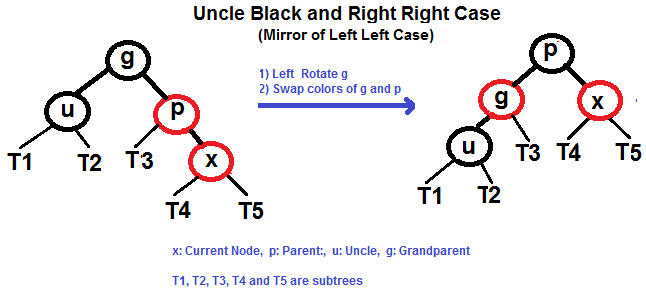
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3d.png)
+
+#### Right Right Case (See g, p and x)
+
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3c.png)
+
+#### Right Left Case (See g, p and x)
+
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3c.png)
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Red%E2%80%93black_tree)
+- [Red Black Tree Insertion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=UaLIHuR1t8Q&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=63)
+- [Red Black Tree Deletion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=CTvfzU_uNKE&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=64)
+- [Red Black Tree Insertion on GeeksForGeeks](https://www.geeksforgeeks.org/red-black-tree-set-2-insert/)
+- [Red Black Tree Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/RedBlack.html)
--- a/src/data-structures/tree/red-black-tree/RedBlackTree.js
+++ b/src/data-structures/tree/red-black-tree/RedBlackTree.js
@ -0,0 +1,315 @@
+import BinarySearchTree from '../binary-search-tree/BinarySearchTree';
+
+// Possible colors of red-black tree nodes.
+const RED_BLACK_TREE_COLORS = {
+  red: 'red',
+  black: 'black',
+};
+
+// Color property name in meta information of the nodes.
+const COLOR_PROP_NAME = 'color';
+
+export default class RedBlackTree extends BinarySearchTree {
+  /**
+   * @param {*} value
+   * @return {BinarySearchTreeNode}
+   */
+  insert(value) {
+    const insertedNode = super.insert(value);
+
+    // if (!this.root.left && !this.root.right) {
+    if (this.nodeComparator.equal(insertedNode, this.root)) {
+      // Make root to always be black.
+      this.makeNodeBlack(insertedNode);
+    } else {
+      // Make all newly inserted nodes to be red.
+      this.makeNodeRed(insertedNode);
+    }
+
+    // Check all conditions and balance the node.
+    this.balance(insertedNode);
+
+    return insertedNode;
+  }
+
+  /**
+   * @param {BinarySearchTreeNode} node
+   */
+  balance(node) {
+    // If it is a root node then nothing to balance here.
+    if (this.nodeComparator.equal(node, this.root)) {
+      return;
+    }
+
+    // If the parent is black then done. Nothing to balance here.
+    if (this.isNodeBlack(node.parent)) {
+      return;
+    }
+
+    const grandParent = node.parent.parent;
+
+    if (node.uncle && this.isNodeRed(node.uncle)) {
+      // If node has red uncle then we need to do RECOLORING.
+
+      // Recolor parent and uncle to black.
+      this.makeNodeBlack(node.uncle);
+      this.makeNodeBlack(node.parent);
+
+      if (!this.nodeComparator.equal(grandParent, this.root)) {
+        // Recolor grand-parent to red if it is not root.
+        this.makeNodeRed(grandParent);
+      } else {
+        // If grand-parent is black root don't do anything.
+        // Since root already has two black sibling that we've just recolored.
+        return;
+      }
+
+      // Now do further checking for recolored grand-parent.
+      this.balance(grandParent);
+    } else if (!node.uncle || this.isNodeBlack(node.uncle)) {
+      // If node uncle is black or absent then we need to do ROTATIONS.
+
+      if (grandParent) {
+        // Grand parent that we will receive after rotations.
+        let newGrandParent;
+
+        if (this.nodeComparator.equal(grandParent.left, node.parent)) {
+          // Left case.
+          if (this.nodeComparator.equal(node.parent.left, node)) {
+            // Left-left case.
+            newGrandParent = this.leftLeftRotation(grandParent);
+          } else {
+            // Left-right case.
+            newGrandParent = this.leftRightRotation(grandParent);
+          }
+        } else {
+          // Right case.
+          if (this.nodeComparator.equal(node.parent.right, node)) {
+            // Right-right case.
+            newGrandParent = this.rightRightRotation(grandParent);
+          } else {
+            // Right-left case.
+            newGrandParent = this.rightLeftRotation(grandParent);
+          }
+        }
+
+        // Set newGrandParent as a root if it doesn't have parent.
+        if (newGrandParent && newGrandParent.parent === null) {
+          this.root = newGrandParent;
+
+          // Recolor root into black.
+          this.makeNodeBlack(this.root);
+        }
+
+        // Check if new grand parent don't violate red-black-tree rules.
+        this.balance(newGrandParent);
+      }
+    }
+  }
+
+  /**
+   * Left Left Case (p is left child of g and x is left child of p)
+   * @param {BinarySearchTreeNode|BinaryTreeNode} grandParentNode
+   * @return {BinarySearchTreeNode}
+   */
+  leftLeftRotation(grandParentNode) {
+    // Memorize the parent of grand-parent node.
+    const grandGrandParent = grandParentNode.parent;
+
+    // Check what type of sibling is our grandParentNode is (left or right).
+    let grandParentNodeIsLeft;
+    if (grandGrandParent) {
+      grandParentNodeIsLeft = this.nodeComparator.equal(grandGrandParent.left, grandParentNode);
+    }
+
+    // Memorize grandParentNode's left node.
+    const parentNode = grandParentNode.left;
+
+    // Memorize parent's right node since we're going to transfer it to
+    // grand parent's left subtree.
+    const parentRightNode = parentNode.right;
+
+    // Make grandParentNode to be right child of parentNode.
+    parentNode.setRight(grandParentNode);
+
+    // Move child's right subtree to grandParentNode's left subtree.
+    grandParentNode.setLeft(parentRightNode);
+
+    // Put parentNode node in place of grandParentNode.
+    if (grandGrandParent) {
+      if (grandParentNodeIsLeft) {
+        grandGrandParent.setLeft(parentNode);
+      } else {
+        grandGrandParent.setRight(parentNode);
+      }
+    } else {
+      // Make parent node a root
+      parentNode.parent = null;
+    }
+
+    // Swap colors of granParent and parent nodes.
+    this.swapNodeColors(parentNode, grandParentNode);
+
+    // Return new root node.
+    return parentNode;
+  }
+
+  /**
+   * Left Right Case (p is left child of g and x is right child of p)
+   * @param {BinarySearchTreeNode|BinaryTreeNode} grandParentNode
+   * @return {BinarySearchTreeNode}
+   */
+  leftRightRotation(grandParentNode) {
+    // Memorize left and left-right nodes.
+    const parentNode = grandParentNode.left;
+    const childNode = parentNode.right;
+
+    // We need to memorize child left node to prevent losing
+    // left child subtree. Later it will be re-assigned to
+    // parent's right sub-tree.
+    const childLeftNode = childNode.left;
+
+    // Make parentNode to be a left child of childNode node.
+    childNode.setLeft(parentNode);
+
+    // Move child's left subtree to parent's right subtree.
+    parentNode.setRight(childLeftNode);
+
+    // Put left-right node in place of left node.
+    grandParentNode.setLeft(childNode);
+
+    // Now we're ready to do left-left rotation.
+    return this.leftLeftRotation(grandParentNode);
+  }
+
+  /**
+   * Right Right Case (p is right child of g and x is right child of p)
+   * @param {BinarySearchTreeNode|BinaryTreeNode} grandParentNode
+   * @return {BinarySearchTreeNode}
+   */
+  rightRightRotation(grandParentNode) {
+    // Memorize the parent of grand-parent node.
+    const grandGrandParent = grandParentNode.parent;
+
+    // Check what type of sibling is our grandParentNode is (left or right).
+    let grandParentNodeIsLeft;
+    if (grandGrandParent) {
+      grandParentNodeIsLeft = this.nodeComparator.equal(grandGrandParent.left, grandParentNode);
+    }
+
+    // Memorize grandParentNode's right node.
+    const parentNode = grandParentNode.right;
+
+    // Memorize parent's left node since we're going to transfer it to
+    // grand parent's right subtree.
+    const parentLeftNode = parentNode.left;
+
+    // Make grandParentNode to be left child of parentNode.
+    parentNode.setLeft(grandParentNode);
+
+    // Transfer all left nodes from parent to right sub-tree of grandparent.
+    grandParentNode.setRight(parentLeftNode);
+
+    // Put parentNode node in place of grandParentNode.
+    if (grandGrandParent) {
+      if (grandParentNodeIsLeft) {
+        grandGrandParent.setLeft(parentNode);
+      } else {
+        grandGrandParent.setRight(parentNode);
+      }
+    } else {
+      // Make parent node a root.
+      parentNode.parent = null;
+    }
+
+    // Swap colors of granParent and parent nodes.
+    this.swapNodeColors(parentNode, grandParentNode);
+
+    // Return new root node.
+    return parentNode;
+  }
+
+  /**
+   * Right Left Case (p is right child of g and x is left child of p)
+   * @param {BinarySearchTreeNode|BinaryTreeNode} grandParentNode
+   * @return {BinarySearchTreeNode}
+   */
+  rightLeftRotation(grandParentNode) {
+    // Memorize right and right-left nodes.
+    const parentNode = grandParentNode.right;
+    const childNode = parentNode.left;
+
+    // We need to memorize child right node to prevent losing
+    // right child subtree. Later it will be re-assigned to
+    // parent's left sub-tree.
+    const childRightNode = childNode.right;
+
+    // Make parentNode to be a right child of childNode.
+    childNode.setRight(parentNode);
+
+    // Move child's right subtree to parent's left subtree.
+    parentNode.setLeft(childRightNode);
+
+    // Put childNode node in place of parentNode.
+    grandParentNode.setRight(childNode);
+
+    // Now we're ready to do right-right rotation.
+    return this.rightRightRotation(grandParentNode);
+  }
+
+  /**
+   * @param {BinarySearchTreeNode|BinaryTreeNode} node
+   * @return {BinarySearchTreeNode}
+   */
+  makeNodeRed(node) {
+    node.meta.set(COLOR_PROP_NAME, RED_BLACK_TREE_COLORS.red);
+
+    return node;
+  }
+
+  /**
+   * @param {BinarySearchTreeNode|BinaryTreeNode} node
+   * @return {BinarySearchTreeNode}
+   */
+  makeNodeBlack(node) {
+    node.meta.set(COLOR_PROP_NAME, RED_BLACK_TREE_COLORS.black);
+
+    return node;
+  }
+
+  /**
+   * @param {BinarySearchTreeNode|BinaryTreeNode} node
+   * @return {boolean}
+   */
+  isNodeRed(node) {
+    return node.meta.get(COLOR_PROP_NAME) === RED_BLACK_TREE_COLORS.red;
+  }
+
+  /**
+   * @param {BinarySearchTreeNode|BinaryTreeNode} node
+   * @return {boolean}
+   */
+  isNodeBlack(node) {
+    return node.meta.get(COLOR_PROP_NAME) === RED_BLACK_TREE_COLORS.black;
+  }
+
+  /**
+   * @param {BinarySearchTreeNode|BinaryTreeNode} node
+   * @return {boolean}
+   */
+  isNodeColored(node) {
+    return this.isNodeRed(node) || this.isNodeBlack(node);
+  }
+
+  /**
+   * @param {BinarySearchTreeNode|BinaryTreeNode} firstNode
+   * @param {BinarySearchTreeNode|BinaryTreeNode} secondNode
+   */
+  swapNodeColors(firstNode, secondNode) {
+    const firstColor = firstNode.meta.get(COLOR_PROP_NAME);
+    const secondColor = secondNode.meta.get(COLOR_PROP_NAME);
+
+    firstNode.meta.set(COLOR_PROP_NAME, secondColor);
+    secondNode.meta.set(COLOR_PROP_NAME, firstColor);
+  }
+}
--- a/src/data-structures/tree/red-black-tree/test/RedBlackTree.test.js
+++ b/src/data-structures/tree/red-black-tree/test/RedBlackTree.test.js
@ -0,0 +1,288 @@
+import RedBlackTree from '../RedBlackTree';
+
+describe('RedBlackTree', () => {
+  it('should always color first inserted node as black', () => {
+    const tree = new RedBlackTree();
+
+    const firstInsertedNode = tree.insert(10);
+
+    expect(tree.isNodeColored(firstInsertedNode)).toBeTruthy();
+    expect(tree.isNodeBlack(firstInsertedNode)).toBeTruthy();
+    expect(tree.isNodeRed(firstInsertedNode)).toBeFalsy();
+
+    expect(tree.toString()).toBe('10');
+    expect(tree.root.height).toBe(0);
+  });
+
+  it('should always color new leaf node as red', () => {
+    const tree = new RedBlackTree();
+
+    const firstInsertedNode = tree.insert(10);
+    const secondInsertedNode = tree.insert(15);
+    const thirdInsertedNode = tree.insert(5);
+
+    expect(tree.isNodeBlack(firstInsertedNode)).toBeTruthy();
+    expect(tree.isNodeRed(secondInsertedNode)).toBeTruthy();
+    expect(tree.isNodeRed(thirdInsertedNode)).toBeTruthy();
+
+    expect(tree.toString()).toBe('5,10,15');
+    expect(tree.root.height).toBe(1);
+  });
+
+  it('should balance itself', () => {
+    const tree = new RedBlackTree();
+
+    tree.insert(5);
+    tree.insert(10);
+    tree.insert(15);
+    tree.insert(20);
+    tree.insert(25);
+    tree.insert(30);
+
+    expect(tree.toString()).toBe('5,10,15,20,25,30');
+    expect(tree.root.height).toBe(3);
+  });
+
+  it('should balance itself when parent is black', () => {
+    const tree = new RedBlackTree();
+
+    const node1 = tree.insert(10);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+
+    const node2 = tree.insert(-10);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+    expect(tree.isNodeRed(node2)).toBeTruthy();
+
+    const node3 = tree.insert(20);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+    expect(tree.isNodeRed(node2)).toBeTruthy();
+    expect(tree.isNodeRed(node3)).toBeTruthy();
+
+    const node4 = tree.insert(-20);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+    expect(tree.isNodeBlack(node2)).toBeTruthy();
+    expect(tree.isNodeBlack(node3)).toBeTruthy();
+    expect(tree.isNodeRed(node4)).toBeTruthy();
+
+    const node5 = tree.insert(25);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+    expect(tree.isNodeBlack(node2)).toBeTruthy();
+    expect(tree.isNodeBlack(node3)).toBeTruthy();
+    expect(tree.isNodeRed(node4)).toBeTruthy();
+    expect(tree.isNodeRed(node5)).toBeTruthy();
+
+    const node6 = tree.insert(6);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+    expect(tree.isNodeBlack(node2)).toBeTruthy();
+    expect(tree.isNodeBlack(node3)).toBeTruthy();
+    expect(tree.isNodeRed(node4)).toBeTruthy();
+    expect(tree.isNodeRed(node5)).toBeTruthy();
+    expect(tree.isNodeRed(node6)).toBeTruthy();
+
+    expect(tree.toString()).toBe('-20,-10,6,10,20,25');
+    expect(tree.root.height).toBe(2);
+
+    const node7 = tree.insert(4);
+
+    expect(tree.root.left.value).toEqual(node2.value);
+
+    expect(tree.toString()).toBe('-20,-10,4,6,10,20,25');
+    expect(tree.root.height).toBe(3);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+    expect(tree.isNodeRed(node2)).toBeTruthy();
+    expect(tree.isNodeBlack(node3)).toBeTruthy();
+    expect(tree.isNodeBlack(node4)).toBeTruthy();
+    expect(tree.isNodeBlack(node4)).toBeTruthy();
+    expect(tree.isNodeRed(node5)).toBeTruthy();
+    expect(tree.isNodeBlack(node6)).toBeTruthy();
+    expect(tree.isNodeRed(node7)).toBeTruthy();
+  });
+
+  it('should balance itself when uncle is red', () => {
+    const tree = new RedBlackTree();
+
+    const node1 = tree.insert(10);
+    const node2 = tree.insert(-10);
+    const node3 = tree.insert(20);
+    const node4 = tree.insert(-20);
+    const node5 = tree.insert(6);
+    const node6 = tree.insert(15);
+    const node7 = tree.insert(25);
+    const node8 = tree.insert(2);
+    const node9 = tree.insert(8);
+
+    expect(tree.toString()).toBe('-20,-10,2,6,8,10,15,20,25');
+    expect(tree.root.height).toBe(3);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+    expect(tree.isNodeRed(node2)).toBeTruthy();
+    expect(tree.isNodeBlack(node3)).toBeTruthy();
+    expect(tree.isNodeBlack(node4)).toBeTruthy();
+    expect(tree.isNodeBlack(node5)).toBeTruthy();
+    expect(tree.isNodeRed(node6)).toBeTruthy();
+    expect(tree.isNodeRed(node7)).toBeTruthy();
+    expect(tree.isNodeRed(node8)).toBeTruthy();
+    expect(tree.isNodeRed(node9)).toBeTruthy();
+
+    const node10 = tree.insert(4);
+
+    expect(tree.toString()).toBe('-20,-10,2,4,6,8,10,15,20,25');
+    expect(tree.root.height).toBe(3);
+
+    expect(tree.root.value).toBe(node5.value);
+
+    expect(tree.isNodeBlack(node5)).toBeTruthy();
+    expect(tree.isNodeRed(node1)).toBeTruthy();
+    expect(tree.isNodeRed(node2)).toBeTruthy();
+    expect(tree.isNodeRed(node10)).toBeTruthy();
+    expect(tree.isNodeRed(node6)).toBeTruthy();
+    expect(tree.isNodeRed(node7)).toBeTruthy();
+    expect(tree.isNodeBlack(node4)).toBeTruthy();
+    expect(tree.isNodeBlack(node8)).toBeTruthy();
+    expect(tree.isNodeBlack(node9)).toBeTruthy();
+    expect(tree.isNodeBlack(node3)).toBeTruthy();
+  });
+
+  it('should do left-left rotation', () => {
+    const tree = new RedBlackTree();
+
+    const node1 = tree.insert(10);
+    const node2 = tree.insert(-10);
+    const node3 = tree.insert(20);
+    const node4 = tree.insert(7);
+    const node5 = tree.insert(15);
+
+    expect(tree.toString()).toBe('-10,7,10,15,20');
+    expect(tree.root.height).toBe(2);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+    expect(tree.isNodeBlack(node2)).toBeTruthy();
+    expect(tree.isNodeBlack(node3)).toBeTruthy();
+    expect(tree.isNodeRed(node4)).toBeTruthy();
+    expect(tree.isNodeRed(node5)).toBeTruthy();
+
+    const node6 = tree.insert(13);
+
+    expect(tree.toString()).toBe('-10,7,10,13,15,20');
+    expect(tree.root.height).toBe(2);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+    expect(tree.isNodeBlack(node2)).toBeTruthy();
+    expect(tree.isNodeBlack(node5)).toBeTruthy();
+    expect(tree.isNodeRed(node4)).toBeTruthy();
+    expect(tree.isNodeRed(node6)).toBeTruthy();
+    expect(tree.isNodeRed(node3)).toBeTruthy();
+  });
+
+  it('should do left-right rotation', () => {
+    const tree = new RedBlackTree();
+
+    const node1 = tree.insert(10);
+    const node2 = tree.insert(-10);
+    const node3 = tree.insert(20);
+    const node4 = tree.insert(7);
+    const node5 = tree.insert(15);
+
+    expect(tree.toString()).toBe('-10,7,10,15,20');
+    expect(tree.root.height).toBe(2);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+    expect(tree.isNodeBlack(node2)).toBeTruthy();
+    expect(tree.isNodeBlack(node3)).toBeTruthy();
+    expect(tree.isNodeRed(node4)).toBeTruthy();
+    expect(tree.isNodeRed(node5)).toBeTruthy();
+
+    const node6 = tree.insert(17);
+
+    expect(tree.toString()).toBe('-10,7,10,15,17,20');
+    expect(tree.root.height).toBe(2);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+    expect(tree.isNodeBlack(node2)).toBeTruthy();
+    expect(tree.isNodeBlack(node6)).toBeTruthy();
+    expect(tree.isNodeRed(node4)).toBeTruthy();
+    expect(tree.isNodeRed(node5)).toBeTruthy();
+    expect(tree.isNodeRed(node3)).toBeTruthy();
+  });
+
+  it('should do recoloring, left-left and left-right rotation', () => {
+    const tree = new RedBlackTree();
+
+    const node1 = tree.insert(10);
+    const node2 = tree.insert(-10);
+    const node3 = tree.insert(20);
+    const node4 = tree.insert(-20);
+    const node5 = tree.insert(6);
+    const node6 = tree.insert(15);
+    const node7 = tree.insert(30);
+    const node8 = tree.insert(1);
+    const node9 = tree.insert(9);
+
+    expect(tree.toString()).toBe('-20,-10,1,6,9,10,15,20,30');
+    expect(tree.root.height).toBe(3);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+    expect(tree.isNodeRed(node2)).toBeTruthy();
+    expect(tree.isNodeBlack(node3)).toBeTruthy();
+    expect(tree.isNodeBlack(node4)).toBeTruthy();
+    expect(tree.isNodeBlack(node5)).toBeTruthy();
+    expect(tree.isNodeRed(node6)).toBeTruthy();
+    expect(tree.isNodeRed(node7)).toBeTruthy();
+    expect(tree.isNodeRed(node8)).toBeTruthy();
+    expect(tree.isNodeRed(node9)).toBeTruthy();
+
+    tree.insert(4);
+
+    expect(tree.toString()).toBe('-20,-10,1,4,6,9,10,15,20,30');
+    expect(tree.root.height).toBe(3);
+  });
+
+  it('should do right-left rotation', () => {
+    const tree = new RedBlackTree();
+
+    const node1 = tree.insert(10);
+    const node2 = tree.insert(-10);
+    const node3 = tree.insert(20);
+    const node4 = tree.insert(-20);
+    const node5 = tree.insert(6);
+    const node6 = tree.insert(30);
+
+    expect(tree.toString()).toBe('-20,-10,6,10,20,30');
+    expect(tree.root.height).toBe(2);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+    expect(tree.isNodeBlack(node2)).toBeTruthy();
+    expect(tree.isNodeBlack(node3)).toBeTruthy();
+    expect(tree.isNodeRed(node4)).toBeTruthy();
+    expect(tree.isNodeRed(node5)).toBeTruthy();
+    expect(tree.isNodeRed(node6)).toBeTruthy();
+
+    const node7 = tree.insert(25);
+
+    const rightNode = tree.root.right;
+    const rightLeftNode = rightNode.left;
+    const rightRightNode = rightNode.right;
+
+    expect(rightNode.value).toBe(node7.value);
+    expect(rightLeftNode.value).toBe(node3.value);
+    expect(rightRightNode.value).toBe(node6.value);
+
+    expect(tree.toString()).toBe('-20,-10,6,10,20,25,30');
+    expect(tree.root.height).toBe(2);
+
+    expect(tree.isNodeBlack(node1)).toBeTruthy();
+    expect(tree.isNodeBlack(node2)).toBeTruthy();
+    expect(tree.isNodeBlack(node7)).toBeTruthy();
+    expect(tree.isNodeRed(node4)).toBeTruthy();
+    expect(tree.isNodeRed(node5)).toBeTruthy();
+    expect(tree.isNodeRed(node3)).toBeTruthy();
+    expect(tree.isNodeRed(node6)).toBeTruthy();
+  });
+});