mirror of
https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git
synced 2024-11-10 11:09:43 +08:00
Merge d2bb607d56 into ca3d16dcce
This commit is contained in:
commit
1f2b2c151d
45
src/algorithms/uncategorized/huffman-coding/README.md
Normal file
45
src/algorithms/uncategorized/huffman-coding/README.md
Normal file
@ -0,0 +1,45 @@
|
|||||||
|
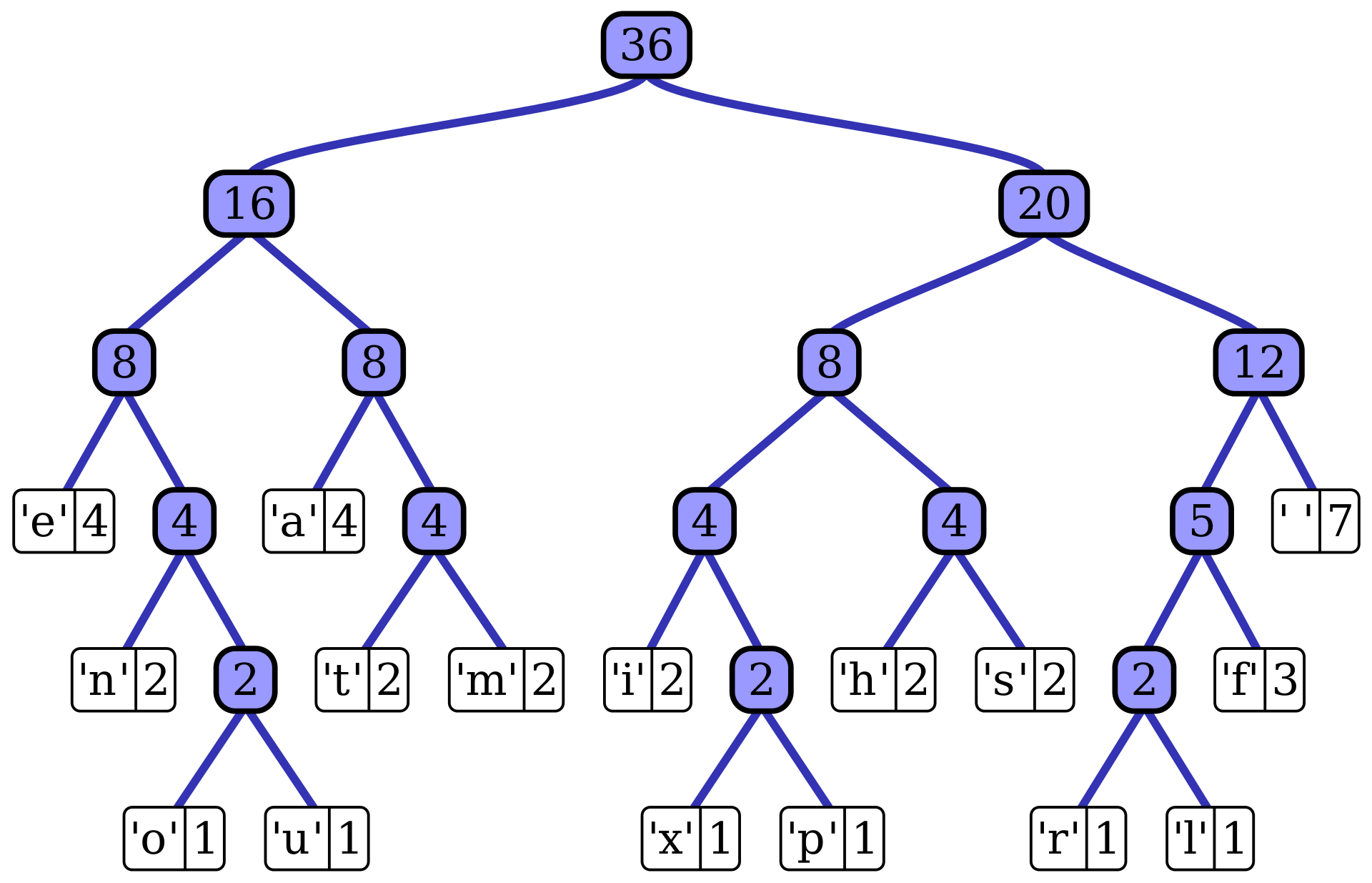
# Huffman Coding Algorithm
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
In computer science and information theory,
|
||||||
|
a Huffman code is a particular type of optimal prefix code
|
||||||
|
that is commonly used for lossless data compression.
|
||||||
|
The process of finding and/or using such a code proceeds by means of Huffman coding, an algorithm developed by David A.
|
||||||
|
Huffman while he was a Sc.D. student at MIT, and published in the 1952
|
||||||
|
paper "A Method for the Construction of Minimum-Redundancy Codes".
|
||||||
|
|
||||||
|
The output from Huffman's algorithm can be viewed as a variable-length code table
|
||||||
|
for encoding a source symbol (such as a character in a file).
|
||||||
|
The algorithm derives this table from the estimated probability or frequency of occurrence (weight)
|
||||||
|
for each possible value of the source symbol.
|
||||||
|
As in other entropy encoding methods,
|
||||||
|
more common symbols are generally represented using fewer bits than less common symbols.
|
||||||
|
Huffman's method can be efficiently implemented,
|
||||||
|
finding a code in time linear to the number of input weights if these weights are sorted.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
## Encode : Compression
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
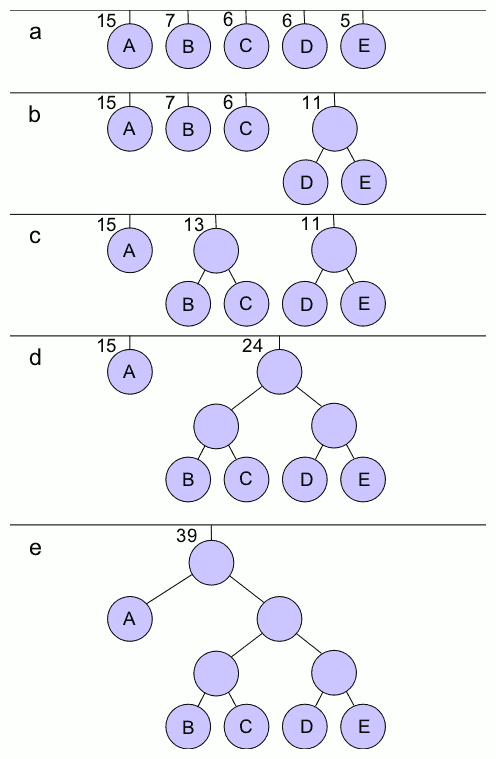
The simplest construction algorithm uses a priority queue where the node with lowest probability is given highest priority:
|
||||||
|
|
||||||
|
1. Create a leaf node for each symbol and add it to the priority queue.
|
||||||
|
2. While there is more than one node in the queue:
|
||||||
|
1. Remove the two nodes of highest priority (lowest probability) from the queue
|
||||||
|
2. Create a new internal node with these two nodes as children and with probability equal to the sum of the two nodes' probabilities.
|
||||||
|
3. Add the new node to the queue.
|
||||||
|
3. The remaining node is the root node and the tree is complete.
|
||||||
|
Since efficient priority queue data structures require `O(log n)` time per insertion, and a tree with `n` leaves has `2n−1` nodes, this algorithm operates in `O(n log n)` time, where `n` is the number of symbols.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
## References
|
||||||
|
|
||||||
|
- [Wikipedia](https://en.wikipedia.org/wiki/Huffman_coding)
|
||||||
|
- [GitHub](https://gist.github.com/1995eaton/86f10f4d0247b4e4e65e)
|
||||||
@ -0,0 +1,133 @@
|
|||||||
|
var Heap = function(fn) {
|
||||||
|
this.fn = fn || function(e) {
|
||||||
|
return e;
|
||||||
|
};
|
||||||
|
this.items = [];
|
||||||
|
};
|
||||||
|
|
||||||
|
Heap.prototype = {
|
||||||
|
swap: function(i, j) {
|
||||||
|
this.items[i] = [
|
||||||
|
this.items[j],
|
||||||
|
this.items[j] = this.items[i]
|
||||||
|
][0];
|
||||||
|
},
|
||||||
|
bubble: function(index) {
|
||||||
|
var parent = ~~((index - 1) / 2);
|
||||||
|
if (this.item(parent) < this.item(index)) {
|
||||||
|
this.swap(index, parent);
|
||||||
|
this.bubble(parent);
|
||||||
|
}
|
||||||
|
},
|
||||||
|
item: function(index) {
|
||||||
|
return this.fn(this.items[index]);
|
||||||
|
},
|
||||||
|
pop: function() {
|
||||||
|
return this.items.pop();
|
||||||
|
},
|
||||||
|
sift: function(index, end) {
|
||||||
|
var child = index * 2 + 1;
|
||||||
|
if (child < end) {
|
||||||
|
if (child + 1 < end && this.item(child + 1) > this.item(child)) {
|
||||||
|
child++;
|
||||||
|
}
|
||||||
|
if (this.item(index) < this.item(child)) {
|
||||||
|
this.swap(index, child);
|
||||||
|
return this.sift(child, end);
|
||||||
|
}
|
||||||
|
}
|
||||||
|
},
|
||||||
|
push: function() {
|
||||||
|
var lastIndex = this.items.length;
|
||||||
|
for (var i = 0; i < arguments.length; i++) {
|
||||||
|
this.items.push(arguments[i]);
|
||||||
|
this.bubble(lastIndex++);
|
||||||
|
}
|
||||||
|
},
|
||||||
|
get length() {
|
||||||
|
return this.items.length;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
|
||||||
|
var Huffman = {
|
||||||
|
// encode function
|
||||||
|
encode: function(data) {
|
||||||
|
var prob = {};
|
||||||
|
var tree = new Heap(function(e) {
|
||||||
|
return e[0];
|
||||||
|
});
|
||||||
|
for (var i = 0; i < data.length; i++) {
|
||||||
|
if (prob.hasOwnProperty(data[i])) {
|
||||||
|
prob[data[i]]++;
|
||||||
|
} else {
|
||||||
|
prob[data[i]] = 1;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
Object.keys(prob).sort(function(a, b) {
|
||||||
|
return ~~(Math.random() * 2);
|
||||||
|
}).forEach(function(e) {
|
||||||
|
tree.push([prob[e], e]);
|
||||||
|
});
|
||||||
|
while (tree.length > 1) {
|
||||||
|
var first = tree.pop(),
|
||||||
|
second = tree.pop();
|
||||||
|
tree.push([first[0] + second[0], [first[1], second[1]]]);
|
||||||
|
}
|
||||||
|
var dict = {};
|
||||||
|
var recurse = function(root, string) {
|
||||||
|
if (root.constructor === Array) {
|
||||||
|
recurse(root[0], string + '0');
|
||||||
|
recurse(root[1], string + '1');
|
||||||
|
} else {
|
||||||
|
dict[root] = string;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
tree.items = tree.pop()[1];
|
||||||
|
recurse(tree.items, '');
|
||||||
|
var result = '';
|
||||||
|
for (var i = 0; i < data.length; i++) {
|
||||||
|
result += dict[data.charAt(i)];
|
||||||
|
}
|
||||||
|
var header = Object.keys(dict).map(function(e) {
|
||||||
|
return e.charCodeAt(0) + '|' + dict[e];
|
||||||
|
}).join('-') + '/';
|
||||||
|
return header + result;
|
||||||
|
},
|
||||||
|
|
||||||
|
// decode function
|
||||||
|
decode: function(string) {
|
||||||
|
string = string.split('/');
|
||||||
|
var data = string[1].split(''),
|
||||||
|
header = {};
|
||||||
|
string[0].split('-').forEach(function(e) {
|
||||||
|
var values = e.split('|');
|
||||||
|
header[values[1]] = String.fromCharCode(values[0]);
|
||||||
|
});
|
||||||
|
var result = '';
|
||||||
|
while (data.length) {
|
||||||
|
var i = 0,
|
||||||
|
cur = '';
|
||||||
|
while (data.length) {
|
||||||
|
cur += data.shift();
|
||||||
|
if (header.hasOwnProperty(cur)) {
|
||||||
|
result += header[cur];
|
||||||
|
break;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
return result;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
|
||||||
|
|
||||||
|
/**** test code ****/
|
||||||
|
var test = 'OSS1234L1OSSTEST'
|
||||||
|
console.log("1. test string = ",test);
|
||||||
|
|
||||||
|
// test encode
|
||||||
|
var enc = Huffman.encode(test);
|
||||||
|
console.log("2. encoded string = ",enc);
|
||||||
|
|
||||||
|
// test decode
|
||||||
|
var dec = Huffman.decode(enc);
|
||||||
|
console.log("3. decoded string = ",dec);
|
||||||
119
src/algorithms/uncategorized/huffman-coding/huffmanCoding.js
Normal file
119
src/algorithms/uncategorized/huffman-coding/huffmanCoding.js
Normal file
@ -0,0 +1,119 @@
|
|||||||
|
var Heap = function(fn) {
|
||||||
|
this.fn = fn || function(e) {
|
||||||
|
return e;
|
||||||
|
};
|
||||||
|
this.items = [];
|
||||||
|
};
|
||||||
|
|
||||||
|
Heap.prototype = {
|
||||||
|
swap: function(i, j) {
|
||||||
|
this.items[i] = [
|
||||||
|
this.items[j],
|
||||||
|
this.items[j] = this.items[i]
|
||||||
|
][0];
|
||||||
|
},
|
||||||
|
bubble: function(index) {
|
||||||
|
var parent = ~~((index - 1) / 2);
|
||||||
|
if (this.item(parent) < this.item(index)) {
|
||||||
|
this.swap(index, parent);
|
||||||
|
this.bubble(parent);
|
||||||
|
}
|
||||||
|
},
|
||||||
|
item: function(index) {
|
||||||
|
return this.fn(this.items[index]);
|
||||||
|
},
|
||||||
|
pop: function() {
|
||||||
|
return this.items.pop();
|
||||||
|
},
|
||||||
|
sift: function(index, end) {
|
||||||
|
var child = index * 2 + 1;
|
||||||
|
if (child < end) {
|
||||||
|
if (child + 1 < end && this.item(child + 1) > this.item(child)) {
|
||||||
|
child++;
|
||||||
|
}
|
||||||
|
if (this.item(index) < this.item(child)) {
|
||||||
|
this.swap(index, child);
|
||||||
|
return this.sift(child, end);
|
||||||
|
}
|
||||||
|
}
|
||||||
|
},
|
||||||
|
push: function() {
|
||||||
|
var lastIndex = this.items.length;
|
||||||
|
for (var i = 0; i < arguments.length; i++) {
|
||||||
|
this.items.push(arguments[i]);
|
||||||
|
this.bubble(lastIndex++);
|
||||||
|
}
|
||||||
|
},
|
||||||
|
get length() {
|
||||||
|
return this.items.length;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
|
||||||
|
var Huffman = {
|
||||||
|
// encode function
|
||||||
|
encode: function(data) {
|
||||||
|
var prob = {};
|
||||||
|
var tree = new Heap(function(e) {
|
||||||
|
return e[0];
|
||||||
|
});
|
||||||
|
for (var i = 0; i < data.length; i++) {
|
||||||
|
if (prob.hasOwnProperty(data[i])) {
|
||||||
|
prob[data[i]]++;
|
||||||
|
} else {
|
||||||
|
prob[data[i]] = 1;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
Object.keys(prob).sort(function(a, b) {
|
||||||
|
return ~~(Math.random() * 2);
|
||||||
|
}).forEach(function(e) {
|
||||||
|
tree.push([prob[e], e]);
|
||||||
|
});
|
||||||
|
while (tree.length > 1) {
|
||||||
|
var first = tree.pop(),
|
||||||
|
second = tree.pop();
|
||||||
|
tree.push([first[0] + second[0], [first[1], second[1]]]);
|
||||||
|
}
|
||||||
|
var dict = {};
|
||||||
|
var recurse = function(root, string) {
|
||||||
|
if (root.constructor === Array) {
|
||||||
|
recurse(root[0], string + '0');
|
||||||
|
recurse(root[1], string + '1');
|
||||||
|
} else {
|
||||||
|
dict[root] = string;
|
||||||
|
}
|
||||||
|
};
|
||||||
|
tree.items = tree.pop()[1];
|
||||||
|
recurse(tree.items, '');
|
||||||
|
var result = '';
|
||||||
|
for (var i = 0; i < data.length; i++) {
|
||||||
|
result += dict[data.charAt(i)];
|
||||||
|
}
|
||||||
|
var header = Object.keys(dict).map(function(e) {
|
||||||
|
return e.charCodeAt(0) + '|' + dict[e];
|
||||||
|
}).join('-') + '/';
|
||||||
|
return header + result;
|
||||||
|
},
|
||||||
|
// decode function
|
||||||
|
decode: function(string) {
|
||||||
|
string = string.split('/');
|
||||||
|
var data = string[1].split(''),
|
||||||
|
header = {};
|
||||||
|
string[0].split('-').forEach(function(e) {
|
||||||
|
var values = e.split('|');
|
||||||
|
header[values[1]] = String.fromCharCode(values[0]);
|
||||||
|
});
|
||||||
|
var result = '';
|
||||||
|
while (data.length) {
|
||||||
|
var i = 0,
|
||||||
|
cur = '';
|
||||||
|
while (data.length) {
|
||||||
|
cur += data.shift();
|
||||||
|
if (header.hasOwnProperty(cur)) {
|
||||||
|
result += header[cur];
|
||||||
|
break;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
}
|
||||||
|
return result;
|
||||||
|
}
|
||||||
|
};
|
||||||
Loading…
Reference in New Issue
Block a user