Add Matrices section with basic Matrix operations (multiplication, transposition, etc.)

README.md

@@ -77,6 +77,7 @@ a set of rules that precisely define a sequence of operations.
   * `B` [Radian & Degree](src/algorithms/math/radian) - radians to degree and backwards conversion
   * `B` [Fast Powering](src/algorithms/math/fast-powering)
   * `B` [Horner's method](src/algorithms/math/horner-method) - polynomial evaluation
+  * `B` [Matrices](src/algorithms/math/matrix) - matrices and basic matrix operations (multiplication, transposition, etc.)
   * `A` [Integer Partition](src/algorithms/math/integer-partition)
   * `A` [Square Root](src/algorithms/math/square-root) - Newton's method
   * `A` [Liu Hui π Algorithm](src/algorithms/math/liu-hui) - approximate π calculations based on N-gons

src/algorithms/cryptography/hill-cipher/hillCipher.js

@@ -1,3 +1,5 @@
+import * as mtrx from '../../math/matrix/Matrix';
+
 // The code of an 'A' character (equals to 65).
 const alphabetCodeShift = 'A'.codePointAt(0);
 const englishAlphabetSize = 26;
@@ -15,33 +17,36 @@ const generateKeyMatrix = (keyString) => {
       'Invalid key string length. The square root of the key string must be an integer',
     );
   }
-  const keyMatrix = [];
   let keyStringIndex = 0;
-  for (let i = 0; i < matrixSize; i += 1) {
-    const keyMatrixRow = [];
-    for (let j = 0; j < matrixSize; j += 1) {
+  return mtrx.generate(
+    [matrixSize, matrixSize],
+    // Callback to get a value of each matrix cell.
+    // The order the matrix is being filled in is from left to right, from top to bottom.
+    () => {
       // A → 0, B → 1, ..., a → 32, b → 33, ...
       const charCodeShifted = (keyString.codePointAt(keyStringIndex)) % alphabetCodeShift;
-      keyMatrixRow.push(charCodeShifted);
       keyStringIndex += 1;
-    }
-    keyMatrix.push(keyMatrixRow);
-  }
-  return keyMatrix;
+      return charCodeShifted;
+    },
+  );
 };
 
 /**
  * Generates a message vector from a given message.
  *
  * @param {string} message - the message to encrypt.
- * @return {number[]} messageVector
+ * @return {number[][]} messageVector
  */
 const generateMessageVector = (message) => {
-  const messageVector = [];
-  for (let i = 0; i < message.length; i += 1) {
-    messageVector.push(message.codePointAt(i) % alphabetCodeShift);
-  }
-  return messageVector;
+  return mtrx.generate(
+    [message.length, 1],
+    // Callback to get a value of each matrix cell.
+    // The order the matrix is being filled in is from left to right, from top to bottom.
+    (cellIndices) => {
+      const rowIndex = cellIndices[0];
+      return message.codePointAt(rowIndex) % alphabetCodeShift;
+    },
+  );
 };
 
 /**
@@ -59,19 +64,17 @@ export function hillCipherEncrypt(message, keyString) {
   }
 
   const keyMatrix = generateKeyMatrix(keyString);
+  const messageVector = generateMessageVector(message);
 
   // keyString.length must equal to square of message.length
   if (keyMatrix.length !== message.length) {
     throw new Error('Invalid key string length. The key length must be a square of message length');
   }
 
-  const messageVector = generateMessageVector(message);
+  const cipherVector = mtrx.dot(keyMatrix, messageVector);
   let cipherString = '';
-  for (let row = 0; row < keyMatrix.length; row += 1) {
-    let item = 0;
-    for (let column = 0; column < keyMatrix.length; column += 1) {
-      item += keyMatrix[row][column] * messageVector[column];
-    }
+  for (let row = 0; row < cipherVector.length; row += 1) {
+    const item = cipherVector[row];
     cipherString += String.fromCharCode((item % englishAlphabetSize) + alphabetCodeShift);
   }
 

src/algorithms/math/matrix/Matrix.js

@@ -0,0 +1,309 @@
+/**
+ * @typedef {number} Cell
+ * @typedef {Cell[][]|Cell[][][]} Matrix
+ * @typedef {number[]} Shape
+ * @typedef {number[]} CellIndices
+ */
+
+/**
+ * Gets the matrix's shape.
+ *
+ * @param {Matrix} m
+ * @returns {Shape}
+ */
+export const shape = (m) => {
+  const shapes = [];
+  let dimension = m;
+  while (dimension && Array.isArray(dimension)) {
+    shapes.push(dimension.length);
+    dimension = (dimension.length && [...dimension][0]) || null;
+  }
+  return shapes;
+};
+
+/**
+ * Checks if matrix has a correct type.
+ *
+ * @param {Matrix} m
+ * @throws {Error}
+ */
+const validateType = (m) => {
+  if (
+    !m
+    || !Array.isArray(m)
+    || !Array.isArray(m[0])
+  ) {
+    throw new Error('Invalid matrix format');
+  }
+};
+
+/**
+ * Checks if matrix is two dimensional.
+ *
+ * @param {Matrix} m
+ * @throws {Error}
+ */
+const validate2D = (m) => {
+  validateType(m);
+  const aShape = shape(m);
+  if (aShape.length !== 2) {
+    throw new Error('Matrix is not of 2D shape');
+  }
+};
+
+/**
+ * Validates that matrices are of the same shape.
+ *
+ * @param {Matrix} a
+ * @param {Matrix} b
+ * @trows {Error}
+ */
+const validateSameShape = (a, b) => {
+  validateType(a);
+  validateType(b);
+
+  const aShape = shape(a);
+  const bShape = shape(b);
+
+  if (aShape.length !== bShape.length) {
+    throw new Error('Matrices have different dimensions');
+  }
+
+  while (aShape.length && bShape.length) {
+    if (aShape.pop() !== bShape.pop()) {
+      throw new Error('Matrices have different shapes');
+    }
+  }
+};
+
+/**
+ * Generates the matrix of specific shape with specific values.
+ *
+ * @param {Shape} mShape - the shape of the matrix to generate
+ * @param {function({CellIndex}): Cell} fill - cell values of a generated matrix.
+ * @returns {Matrix}
+ */
+export const generate = (mShape, fill) => {
+  /**
+   * Generates the matrix recursively.
+   *
+   * @param {Shape} recShape - the shape of the matrix to generate
+   * @param {CellIndices} recIndices
+   * @returns {Matrix}
+   */
+  const generateRecursively = (recShape, recIndices) => {
+    if (recShape.length === 1) {
+      return Array(recShape[0])
+        .fill(null)
+        .map((cellValue, cellIndex) => fill([...recIndices, cellIndex]));
+    }
+    const m = [];
+    for (let i = 0; i < recShape[0]; i += 1) {
+      m.push(generateRecursively(recShape.slice(1), [...recIndices, i]));
+    }
+    return m;
+  };
+
+  return generateRecursively(mShape, []);
+};
+
+/**
+ * Generates the matrix of zeros of specified shape.
+ *
+ * @param {Shape} mShape - shape of the matrix
+ * @returns {Matrix}
+ */
+export const zeros = (mShape) => {
+  return generate(mShape, () => 0);
+};
+
+/**
+ * @param {Matrix} a
+ * @param {Matrix} b
+ * @return Matrix
+ * @throws {Error}
+ */
+export const dot = (a, b) => {
+  // Validate inputs.
+  validate2D(a);
+  validate2D(b);
+
+  // Check dimensions.
+  const aShape = shape(a);
+  const bShape = shape(b);
+  if (aShape[1] !== bShape[0]) {
+    throw new Error('Matrices have incompatible shape for multiplication');
+  }
+
+  // Perform matrix multiplication.
+  const outputShape = [aShape[0], bShape[1]];
+  const c = zeros(outputShape);
+
+  for (let bCol = 0; bCol < b[0].length; bCol += 1) {
+    for (let aRow = 0; aRow < a.length; aRow += 1) {
+      let cellSum = 0;
+      for (let aCol = 0; aCol < a[aRow].length; aCol += 1) {
+        cellSum += a[aRow][aCol] * b[aCol][bCol];
+      }
+      c[aRow][bCol] = cellSum;
+    }
+  }
+
+  return c;
+};
+
+/**
+ * Transposes the matrix.
+ *
+ * @param {Matrix} m
+ * @returns Matrix
+ * @throws {Error}
+ */
+export const t = (m) => {
+  validate2D(m);
+  const mShape = shape(m);
+  const transposed = zeros([mShape[1], mShape[0]]);
+  for (let row = 0; row < m.length; row += 1) {
+    for (let col = 0; col < m[0].length; col += 1) {
+      transposed[col][row] = m[row][col];
+    }
+  }
+  return transposed;
+};
+
+/**
+ * Traverses the matrix.
+ *
+ * @param {Matrix} m
+ * @param {function(indices: CellIndices, c: Cell)} visit
+ */
+const walk = (m, visit) => {
+  /**
+   * Traverses the matrix recursively.
+   *
+   * @param {Matrix} recM
+   * @param {CellIndices} cellIndices
+   * @return {Matrix}
+   */
+  const recWalk = (recM, cellIndices) => {
+    const recMShape = shape(recM);
+
+    if (recMShape.length === 1) {
+      for (let i = 0; i < recM.length; i += 1) {
+        visit([...cellIndices, i], recM[i]);
+      }
+    }
+    for (let i = 0; i < recM.length; i += 1) {
+      recWalk(recM[i], [...cellIndices, i]);
+    }
+  };
+
+  recWalk(m, []);
+};
+
+/**
+ * Gets the matrix cell value at specific index.
+ *
+ * @param {Matrix} m - Matrix that contains the cell that needs to be updated
+ * @param {CellIndices} cellIndices - Array of cell indices
+ * @return {Cell}
+ */
+const getCellAtIndex = (m, cellIndices) => {
+  // We start from the row at specific index.
+  let cell = m[cellIndices[0]];
+  // Going deeper into the next dimensions but not to the last one to preserve
+  // the pointer to the last dimension array.
+  for (let dimIdx = 1; dimIdx < cellIndices.length - 1; dimIdx += 1) {
+    cell = cell[cellIndices[dimIdx]];
+  }
+  // At this moment the cell variable points to the array at the last needed dimension.
+  return cell[cellIndices[cellIndices.length - 1]];
+};
+
+/**
+ * Update the matrix cell at specific index.
+ *
+ * @param {Matrix} m - Matrix that contains the cell that needs to be updated
+ * @param {CellIndices} cellIndices - Array of cell indices
+ * @param {Cell} cellValue - New cell value
+ */
+const updateCellAtIndex = (m, cellIndices, cellValue) => {
+  // We start from the row at specific index.
+  let cell = m[cellIndices[0]];
+  // Going deeper into the next dimensions but not to the last one to preserve
+  // the pointer to the last dimension array.
+  for (let dimIdx = 1; dimIdx < cellIndices.length - 1; dimIdx += 1) {
+    cell = cell[cellIndices[dimIdx]];
+  }
+  // At this moment the cell variable points to the array at the last needed dimension.
+  cell[cellIndices[cellIndices.length - 1]] = cellValue;
+};
+
+/**
+ * Adds two matrices element-wise.
+ *
+ * @param {Matrix} a
+ * @param {Matrix} b
+ * @return {Matrix}
+ */
+export const add = (a, b) => {
+  validateSameShape(a, b);
+  const result = zeros(shape(a));
+
+  walk(a, (cellIndices, cellValue) => {
+    updateCellAtIndex(result, cellIndices, cellValue);
+  });
+
+  walk(b, (cellIndices, cellValue) => {
+    const currentCellValue = getCellAtIndex(result, cellIndices);
+    updateCellAtIndex(result, cellIndices, currentCellValue + cellValue);
+  });
+
+  return result;
+};
+
+/**
+ * Multiplies two matrices element-wise.
+ *
+ * @param {Matrix} a
+ * @param {Matrix} b
+ * @return {Matrix}
+ */
+export const mul = (a, b) => {
+  validateSameShape(a, b);
+  const result = zeros(shape(a));
+
+  walk(a, (cellIndices, cellValue) => {
+    updateCellAtIndex(result, cellIndices, cellValue);
+  });
+
+  walk(b, (cellIndices, cellValue) => {
+    const currentCellValue = getCellAtIndex(result, cellIndices);
+    updateCellAtIndex(result, cellIndices, currentCellValue * cellValue);
+  });
+
+  return result;
+};
+
+/**
+ * Subtract two matrices element-wise.
+ *
+ * @param {Matrix} a
+ * @param {Matrix} b
+ * @return {Matrix}
+ */
+export const sub = (a, b) => {
+  validateSameShape(a, b);
+  const result = zeros(shape(a));
+
+  walk(a, (cellIndices, cellValue) => {
+    updateCellAtIndex(result, cellIndices, cellValue);
+  });
+
+  walk(b, (cellIndices, cellValue) => {
+    const currentCellValue = getCellAtIndex(result, cellIndices);
+    updateCellAtIndex(result, cellIndices, currentCellValue - cellValue);
+  });
+
+  return result;
+};

src/algorithms/math/matrix/README.md

@@ -0,0 +1,63 @@
+# Matrices
+
+In mathematics, a **matrix** (plural **matrices**) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns. For example, the dimension of the matrix below is `2 × 3` (read "two by three"), because there are two rows and three columns:
+
+```
+| 1  9 -13 |
+| 20 5 -6  |
+```
+
+![An `m × n` matrix](https://upload.wikimedia.org/wikipedia/commons/b/bf/Matris.png)
+
+An `m × n` matrix: the `m` rows are horizontal, and the `n` columns are vertical. Each element of a matrix is often denoted by a variable with two subscripts. For example, <i>a<sub>2,1</sub></i> represents the element at the second row and first column of the matrix
+
+## Operations on matrices
+
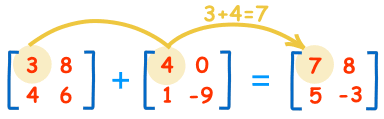
+### Addition
+
+To add two matrices: add the numbers in the matching positions:
+
+![Matrices addition](https://www.mathsisfun.com/algebra/images/matrix-addition.gif)
+
+The two matrices must be the same size, i.e. the rows must match in size, and the columns must match in size.
+
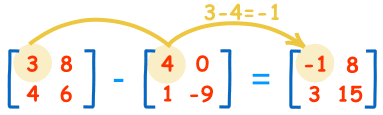
+### Subtracting
+
+To subtract two matrices: subtract the numbers in the matching positions:
+
+![Matrices subtraction](https://www.mathsisfun.com/algebra/images/matrix-subtraction.gif)
+
+### Multiply by a Constant
+
+We can multiply a matrix by a constant (the value 2 in this case):
+
+![Matrices multiplication be a constant](https://www.mathsisfun.com/algebra/images/matrix-multiply-constant.gif)
+
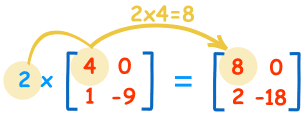
+### Multiplying by Another Matrix
+
+To multiply a matrix by another matrix we need to do the [dot product](https://www.mathsisfun.com/algebra/vectors-dot-product.html) of rows and columns.
+
+To work out the answer for the **1st row** and **1st column**:
+
+![Matrices multiplication - 1st step](https://www.mathsisfun.com/algebra/images/matrix-multiply-a.svg)
+
+Here it is for the 1st row and 2nd column:
+
+![Matrices multiplication - 2st step](https://www.mathsisfun.com/algebra/images/matrix-multiply-b.svg)
+
+If we'll do the same for the rest of the rows and columns we'll get the following resulting matrix:
+
+![Matrices multiplication - Result](https://www.mathsisfun.com/algebra/images/matrix-multiply-c.svg)
+
+### Transposing
+
+To "transpose" a matrix, swap the rows and columns.
+
+We put a "T" in the top right-hand corner to mean transpose:
+
+![Transposing](https://www.mathsisfun.com/algebra/images/matrix-transpose.gif)
+
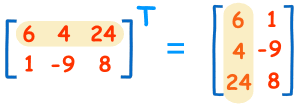
+## References
+
+- [Matrices on MathIsFun](https://www.mathsisfun.com/algebra/matrix-introduction.html)
+- [Matrix on Wikipedia](https://en.wikipedia.org/wiki/Matrix_(mathematics))

src/algorithms/math/matrix/__tests__/Matrix.test.js

@@ -0,0 +1,455 @@
+import * as mtrx from '../Matrix';
+
+describe('Matrix', () => {
+  it('should throw when trying to add matrices of invalid shapes', () => {
+    expect(
+      () => mtrx.dot([0], [1]),
+    ).toThrowError('Invalid matrix format');
+    expect(
+      () => mtrx.dot([[0]], [1]),
+    ).toThrowError('Invalid matrix format');
+    expect(
+      () => mtrx.dot([[[0]]], [[1]]),
+    ).toThrowError('Matrix is not of 2D shape');
+    expect(
+      () => mtrx.dot([[0]], [[1], [2]]),
+    ).toThrowError('Matrices have incompatible shape for multiplication');
+  });
+
+  it('should calculate matrices dimensions', () => {
+    expect(mtrx.shape([])).toEqual([0]);
+
+    expect(mtrx.shape([
+      [],
+    ])).toEqual([1, 0]);
+
+    expect(mtrx.shape([
+      [0],
+    ])).toEqual([1, 1]);
+
+    expect(mtrx.shape([
+      [0, 0],
+    ])).toEqual([1, 2]);
+
+    expect(mtrx.shape([
+      [0, 0],
+      [0, 0],
+    ])).toEqual([2, 2]);
+
+    expect(mtrx.shape([
+      [0, 0, 0],
+      [0, 0, 0],
+    ])).toEqual([2, 3]);
+
+    expect(mtrx.shape([
+      [0, 0],
+      [0, 0],
+      [0, 0],
+    ])).toEqual([3, 2]);
+
+    expect(mtrx.shape([
+      [0, 0, 0],
+      [0, 0, 0],
+      [0, 0, 0],
+    ])).toEqual([3, 3]);
+
+    expect(mtrx.shape([
+      [0],
+      [0],
+      [0],
+    ])).toEqual([3, 1]);
+
+    expect(mtrx.shape([
+      [[0], [0], [0]],
+      [[0], [0], [0]],
+      [[0], [0], [0]],
+    ])).toEqual([3, 3, 1]);
+
+    expect(mtrx.shape([
+      [[0, 0, 0], [0, 0, 0], [0, 0, 0]],
+      [[0, 0, 0], [0, 0, 0], [0, 0, 0]],
+      [[0, 0, 0], [0, 0, 0], [0, 0, 0]],
+    ])).toEqual([3, 3, 3]);
+  });
+
+  it('should generate the matrix of zeros', () => {
+    expect(mtrx.zeros([1, 0])).toEqual([
+      [],
+    ]);
+
+    expect(mtrx.zeros([1, 1])).toEqual([
+      [0],
+    ]);
+
+    expect(mtrx.zeros([1, 3])).toEqual([
+      [0, 0, 0],
+    ]);
+
+    expect(mtrx.zeros([3, 3])).toEqual([
+      [0, 0, 0],
+      [0, 0, 0],
+      [0, 0, 0],
+    ]);
+
+    expect(mtrx.zeros([3, 3, 1])).toEqual([
+      [[0], [0], [0]],
+      [[0], [0], [0]],
+      [[0], [0], [0]],
+    ]);
+  });
+
+  it('should generate the matrix with custom values', () => {
+    expect(mtrx.generate([1, 0], () => 1)).toEqual([
+      [],
+    ]);
+
+    expect(mtrx.generate([1, 1], () => 1)).toEqual([
+      [1],
+    ]);
+
+    expect(mtrx.generate([1, 3], () => 1)).toEqual([
+      [1, 1, 1],
+    ]);
+
+    expect(mtrx.generate([3, 3], () => 1)).toEqual([
+      [1, 1, 1],
+      [1, 1, 1],
+      [1, 1, 1],
+    ]);
+
+    expect(mtrx.generate([3, 3, 1], () => 1)).toEqual([
+      [[1], [1], [1]],
+      [[1], [1], [1]],
+      [[1], [1], [1]],
+    ]);
+  });
+
+  it('should generate a custom matrix based on specific cell indices', () => {
+    const indicesCallback = jest.fn((indices) => {
+      return indices[0] * 10 + indices[1];
+    });
+    const m = mtrx.generate([3, 3], indicesCallback);
+
+    expect(indicesCallback).toHaveBeenCalledTimes(3 * 3);
+    expect(indicesCallback.mock.calls[0][0]).toEqual([0, 0]);
+    expect(indicesCallback.mock.calls[1][0]).toEqual([0, 1]);
+    expect(indicesCallback.mock.calls[2][0]).toEqual([0, 2]);
+    expect(indicesCallback.mock.calls[3][0]).toEqual([1, 0]);
+    expect(indicesCallback.mock.calls[4][0]).toEqual([1, 1]);
+    expect(indicesCallback.mock.calls[5][0]).toEqual([1, 2]);
+    expect(indicesCallback.mock.calls[6][0]).toEqual([2, 0]);
+    expect(indicesCallback.mock.calls[7][0]).toEqual([2, 1]);
+    expect(indicesCallback.mock.calls[8][0]).toEqual([2, 2]);
+    expect(m).toEqual([
+      [0, 1, 2],
+      [10, 11, 12],
+      [20, 21, 22],
+    ]);
+  });
+
+  it('should multiply two matrices', () => {
+    let c;
+    c = mtrx.dot(
+      [
+        [1, 2],
+        [3, 4],
+      ],
+      [
+        [5, 6],
+        [7, 8],
+      ],
+    );
+    expect(mtrx.shape(c)).toEqual([2, 2]);
+    expect(c).toEqual([
+      [19, 22],
+      [43, 50],
+    ]);
+
+    c = mtrx.dot(
+      [
+        [1, 2],
+        [3, 4],
+      ],
+      [
+        [5],
+        [6],
+      ],
+    );
+    expect(mtrx.shape(c)).toEqual([2, 1]);
+    expect(c).toEqual([
+      [17],
+      [39],
+    ]);
+
+    c = mtrx.dot(
+      [
+        [1, 2, 3],
+        [4, 5, 6],
+      ],
+      [
+        [7, 8],
+        [9, 10],
+        [11, 12],
+      ],
+    );
+    expect(mtrx.shape(c)).toEqual([2, 2]);
+    expect(c).toEqual([
+      [58, 64],
+      [139, 154],
+    ]);
+
+    c = mtrx.dot(
+      [
+        [3, 4, 2],
+      ],
+      [
+        [13, 9, 7, 5],
+        [8, 7, 4, 6],
+        [6, 4, 0, 3],
+      ],
+    );
+    expect(mtrx.shape(c)).toEqual([1, 4]);
+    expect(c).toEqual([
+      [83, 63, 37, 45],
+    ]);
+  });
+
+  it('should transpose matrices', () => {
+    expect(mtrx.t([[1, 2, 3]])).toEqual([
+      [1],
+      [2],
+      [3],
+    ]);
+
+    expect(mtrx.t([
+      [1],
+      [2],
+      [3],
+    ])).toEqual([
+      [1, 2, 3],
+    ]);
+
+    expect(mtrx.t([
+      [1, 2, 3],
+      [4, 5, 6],
+    ])).toEqual([
+      [1, 4],
+      [2, 5],
+      [3, 6],
+    ]);
+
+    expect(mtrx.t([
+      [1, 2, 3],
+      [4, 5, 6],
+      [7, 8, 9],
+    ])).toEqual([
+      [1, 4, 7],
+      [2, 5, 8],
+      [3, 6, 9],
+    ]);
+  });
+
+  it('should throw when trying to transpose non 2D matrix', () => {
+    expect(() => {
+      mtrx.t([[[1]]]);
+    }).toThrowError('Matrix is not of 2D shape');
+  });
+
+  it('should add two matrices', () => {
+    expect(mtrx.add([[1]], [[2]])).toEqual([[3]]);
+
+    expect(mtrx.add(
+      [[1, 2, 3]],
+      [[4, 5, 6]],
+    ))
+      .toEqual(
+        [[5, 7, 9]],
+      );
+
+    expect(mtrx.add(
+      [[1], [2], [3]],
+      [[4], [5], [6]],
+    ))
+      .toEqual(
+        [[5], [7], [9]],
+      );
+
+    expect(mtrx.add(
+      [
+        [1, 2, 3],
+        [4, 5, 6],
+        [7, 8, 9],
+      ],
+      [
+        [10, 11, 12],
+        [13, 14, 15],
+        [16, 17, 18],
+      ],
+    ))
+      .toEqual(
+        [
+          [11, 13, 15],
+          [17, 19, 21],
+          [23, 25, 27],
+        ],
+      );
+
+    expect(mtrx.add(
+      [
+        [[1], [2], [3]],
+        [[4], [5], [6]],
+        [[7], [8], [9]],
+      ],
+      [
+        [[10], [11], [12]],
+        [[13], [14], [15]],
+        [[16], [17], [18]],
+      ],
+    ))
+      .toEqual(
+        [
+          [[11], [13], [15]],
+          [[17], [19], [21]],
+          [[23], [25], [27]],
+        ],
+      );
+  });
+
+  it('should throw when trying to add matrices of different shape', () => {
+    expect(() => mtrx.add([[0]], [[[0]]])).toThrowError(
+      'Matrices have different dimensions',
+    );
+
+    expect(() => mtrx.add([[0]], [[0, 0]])).toThrowError(
+      'Matrices have different shapes',
+    );
+  });
+
+  it('should do element wise multiplication two matrices', () => {
+    expect(mtrx.mul([[2]], [[3]])).toEqual([[6]]);
+
+    expect(mtrx.mul(
+      [[1, 2, 3]],
+      [[4, 5, 6]],
+    ))
+      .toEqual(
+        [[4, 10, 18]],
+      );
+
+    expect(mtrx.mul(
+      [[1], [2], [3]],
+      [[4], [5], [6]],
+    ))
+      .toEqual(
+        [[4], [10], [18]],
+      );
+
+    expect(mtrx.mul(
+      [
+        [1, 2],
+        [3, 4],
+      ],
+      [
+        [5, 6],
+        [7, 8],
+      ],
+    ))
+      .toEqual(
+        [
+          [5, 12],
+          [21, 32],
+        ],
+      );
+
+    expect(mtrx.mul(
+      [
+        [[1], [2]],
+        [[3], [4]],
+      ],
+      [
+        [[5], [6]],
+        [[7], [8]],
+      ],
+    ))
+      .toEqual(
+        [
+          [[5], [12]],
+          [[21], [32]],
+        ],
+      );
+  });
+
+  it('should throw when trying to multiply matrices element-wise of different shape', () => {
+    expect(() => mtrx.mul([[0]], [[[0]]])).toThrowError(
+      'Matrices have different dimensions',
+    );
+
+    expect(() => mtrx.mul([[0]], [[0, 0]])).toThrowError(
+      'Matrices have different shapes',
+    );
+  });
+
+  it('should do element wise subtraction two matrices', () => {
+    expect(mtrx.sub([[3]], [[2]])).toEqual([[1]]);
+
+    expect(mtrx.sub(
+      [[10, 12, 14]],
+      [[4, 5, 6]],
+    ))
+      .toEqual(
+        [[6, 7, 8]],
+      );
+
+    expect(mtrx.sub(
+      [[[10], [12], [14]]],
+      [[[4], [5], [6]]],
+    ))
+      .toEqual(
+        [[[6], [7], [8]]],
+      );
+
+    expect(mtrx.sub(
+      [
+        [10, 20],
+        [30, 40],
+      ],
+      [
+        [5, 6],
+        [7, 8],
+      ],
+    ))
+      .toEqual(
+        [
+          [5, 14],
+          [23, 32],
+        ],
+      );
+
+    expect(mtrx.sub(
+      [
+        [[10], [20]],
+        [[30], [40]],
+      ],
+      [
+        [[5], [6]],
+        [[7], [8]],
+      ],
+    ))
+      .toEqual(
+        [
+          [[5], [14]],
+          [[23], [32]],
+        ],
+      );
+  });
+
+  it('should throw when trying to subtract matrices element-wise of different shape', () => {
+    expect(() => mtrx.sub([[0]], [[[0]]])).toThrowError(
+      'Matrices have different dimensions',
+    );
+
+    expect(() => mtrx.sub([[0]], [[0, 0]])).toThrowError(
+      'Matrices have different shapes',
+    );
+  });
+});