mirror of
https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git
synced 2024-12-25 22:46:20 +08:00
Add brute force solution of Rain Terraces problem.
This commit is contained in:
parent
6fc429975f
commit
340a71b7d9
@ -128,7 +128,7 @@ a set of rules that precisely define a sequence of operations.
|
||||
* `B` [Square Matrix Rotation](src/algorithms/uncategorized/square-matrix-rotation) - in-place algorithm
|
||||
* `B` [Jump Game](src/algorithms/uncategorized/jump-game) - backtracking, dynamic programming (top-down + bottom-up) and greedy examples
|
||||
* `B` [Unique Paths](src/algorithms/uncategorized/unique-paths) - backtracking, dynamic programming and Pascal's Triangle based examples
|
||||
* `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - trapping rain water problem
|
||||
* `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - trapping rain water problem (dynamic programming and brute force versions)
|
||||
* `A` [N-Queens Problem](src/algorithms/uncategorized/n-queens)
|
||||
* `A` [Knight's Tour](src/algorithms/uncategorized/knight-tour)
|
||||
|
||||
@ -140,6 +140,7 @@ algorithm is an abstraction higher than a computer program.
|
||||
|
||||
* **Brute Force** - look at all the possibilities and selects the best solution
|
||||
* `B` [Linear Search](src/algorithms/search/linear-search)
|
||||
* `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - trapping rain water problem
|
||||
* `A` [Maximum Subarray](src/algorithms/sets/maximum-subarray)
|
||||
* `A` [Travelling Salesman Problem](src/algorithms/graph/travelling-salesman) - shortest possible route that visits each city and returns to the origin city
|
||||
* **Greedy** - choose the best option at the current time, without any consideration for the future
|
||||
@ -164,6 +165,7 @@ algorithm is an abstraction higher than a computer program.
|
||||
* `B` [Fibonacci Number](src/algorithms/math/fibonacci)
|
||||
* `B` [Jump Game](src/algorithms/uncategorized/jump-game)
|
||||
* `B` [Unique Paths](src/algorithms/uncategorized/unique-paths)
|
||||
* `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - trapping rain water problem
|
||||
* `A` [Levenshtein Distance](src/algorithms/string/levenshtein-distance) - minimum edit distance between two sequences
|
||||
* `A` [Longest Common Subsequence](src/algorithms/sets/longest-common-subsequence) (LCS)
|
||||
* `A` [Longest Common Substring](src/algorithms/string/longest-common-substring)
|
||||
|
||||
@ -62,16 +62,58 @@ be stored in every element of array. For example, consider the array
|
||||
`[3, 0, 0, 2, 0, 4]`, We can trap "3*2 units" of water between 3 an 2, "1 unit"
|
||||
on top of bar 2 and "3 units" between 2 and 4. See below diagram also.
|
||||
|
||||
A **simple solution** is to traverse every array element and find the highest
|
||||
bars on left and right sides. Take the smaller of two heights. The difference
|
||||
between smaller height and height of current element is the amount of water
|
||||
that can be stored in this array element. Time complexity of this solution
|
||||
is `O(n2)`.
|
||||
### Approach 1: Brute force
|
||||
|
||||
An **efficient solution** is to pre-compute highest bar on left and right of
|
||||
every bar in `O(n)` time. Then use these pre-computed values to find the
|
||||
amount of water in every array element.
|
||||
**Intuition**
|
||||
|
||||
For each element in the array, we find the maximum level of water it can trap
|
||||
after the rain, which is equal to the minimum of maximum height of bars on both
|
||||
the sides minus its own height.
|
||||
|
||||
**Steps**
|
||||
|
||||
- Initialize `answer = 0`
|
||||
- Iterate the array from left to right:
|
||||
- Initialize `max_left = 0 and `max_right = 0`
|
||||
- Iterate from the current element to the beginning of array updating: `max_left = max(max_left, height[j])`
|
||||
- Iterate from the current element to the end of array updating: `max_right = max(max_right, height[j])`
|
||||
- Add `min(max_left, max_right) − height[i]` to `answer`
|
||||
|
||||
**Complexity Analysis**
|
||||
|
||||
Time complexity: `O(n^2)`. For each element of array, we iterate the left and right parts.
|
||||
|
||||
Auxiliary space complexity: `O(1)` extra space.
|
||||
|
||||
### Approach 2: Dynamic Programming
|
||||
|
||||
**Intuition**
|
||||
|
||||
In brute force, we iterate over the left and right parts again and again just to
|
||||
find the highest bar size up to that index. But, this could be stored. Voila,
|
||||
dynamic programming.
|
||||
|
||||
So we may pre-compute highest bar on left and right of every bar in `O(n)` time.
|
||||
Then use these pre-computed values to find the amount of water in every array element.
|
||||
|
||||
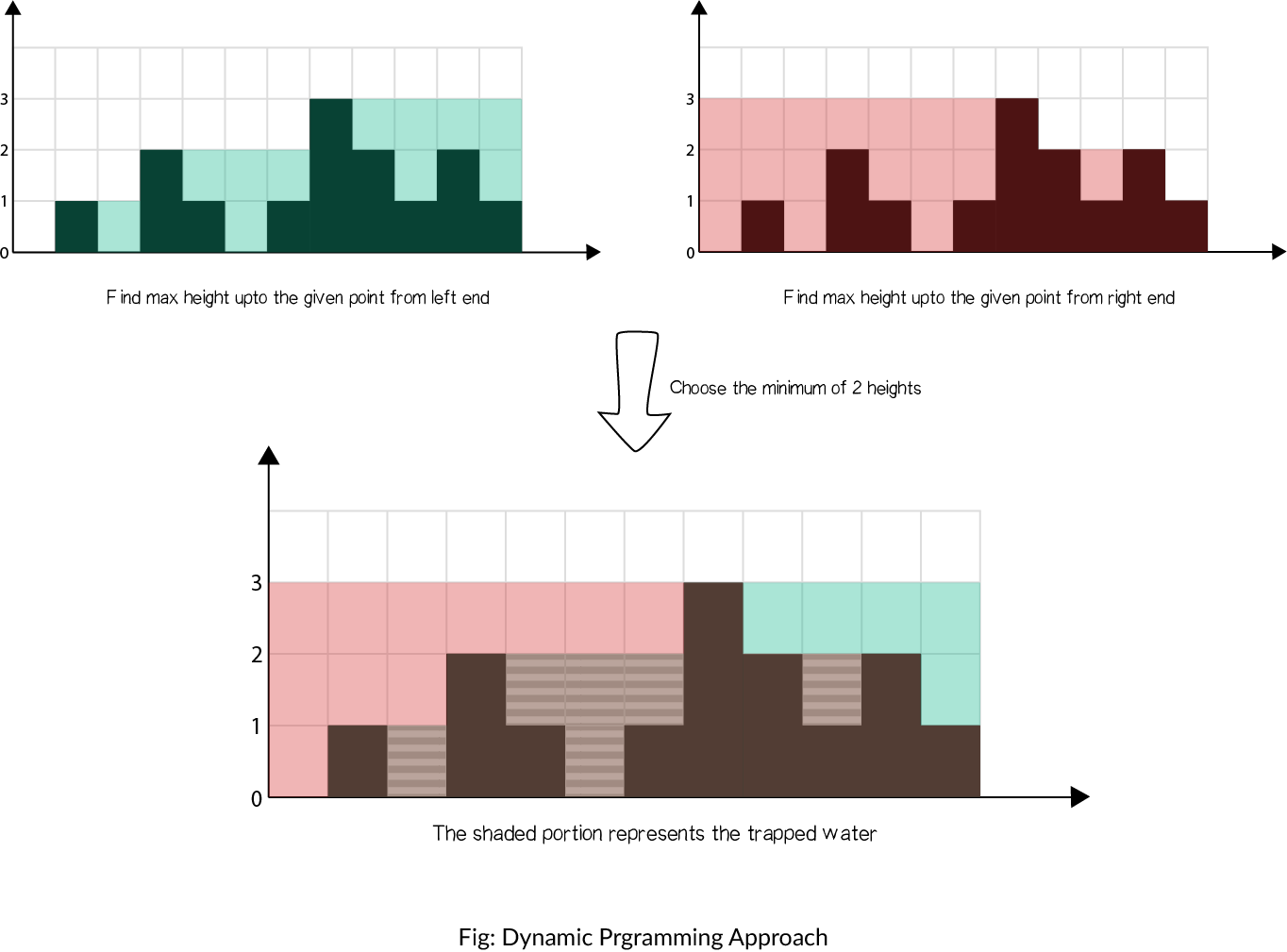
The concept is illustrated as shown:
|
||||
|
||||
|
||||
|
||||
**Steps**
|
||||
|
||||
- Find maximum height of bar from the left end up to an index `i` in the array `left_max`.
|
||||
- Find maximum height of bar from the right end up to an index `i` in the array `right_max`.
|
||||
- Iterate over the `height` array and update `answer`:
|
||||
- Add `min(max_left[i], max_right[i]) − height[i]` to `answer`.
|
||||
|
||||
**Complexity Analysis**
|
||||
|
||||
Time complexity: `O(n)`.
|
||||
|
||||
Auxiliary space complexity: `O(n)` extra space.
|
||||
|
||||
## References
|
||||
|
||||
- [GeeksForGeeks](https://www.geeksforgeeks.org/trapping-rain-water/)
|
||||
- [LeetCode](https://leetcode.com/problems/trapping-rain-water/solution/)
|
||||
|
||||
@ -0,0 +1,21 @@
|
||||
import bfRainTerraces from '../bfRainTerraces';
|
||||
|
||||
describe('bfRainTerraces', () => {
|
||||
it('should find the amount of water collected after raining', () => {
|
||||
expect(bfRainTerraces([1])).toBe(0);
|
||||
expect(bfRainTerraces([1, 0])).toBe(0);
|
||||
expect(bfRainTerraces([0, 1])).toBe(0);
|
||||
expect(bfRainTerraces([0, 1, 0])).toBe(0);
|
||||
expect(bfRainTerraces([0, 1, 0, 0])).toBe(0);
|
||||
expect(bfRainTerraces([0, 1, 0, 0, 1, 0])).toBe(2);
|
||||
expect(bfRainTerraces([0, 2, 0, 0, 1, 0])).toBe(2);
|
||||
expect(bfRainTerraces([2, 0, 2])).toBe(2);
|
||||
expect(bfRainTerraces([2, 0, 5])).toBe(2);
|
||||
expect(bfRainTerraces([3, 0, 0, 2, 0, 4])).toBe(10);
|
||||
expect(bfRainTerraces([0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1])).toBe(6);
|
||||
expect(bfRainTerraces([1, 1, 1, 1, 1])).toBe(0);
|
||||
expect(bfRainTerraces([1, 2, 3, 4, 5])).toBe(0);
|
||||
expect(bfRainTerraces([4, 1, 3, 1, 2, 1, 2, 1])).toBe(4);
|
||||
expect(bfRainTerraces([0, 2, 4, 3, 4, 2, 4, 0, 8, 7, 0])).toBe(7);
|
||||
});
|
||||
});
|
||||
@ -0,0 +1,21 @@
|
||||
import dpRainTerraces from '../dpRainTerraces';
|
||||
|
||||
describe('dpRainTerraces', () => {
|
||||
it('should find the amount of water collected after raining', () => {
|
||||
expect(dpRainTerraces([1])).toBe(0);
|
||||
expect(dpRainTerraces([1, 0])).toBe(0);
|
||||
expect(dpRainTerraces([0, 1])).toBe(0);
|
||||
expect(dpRainTerraces([0, 1, 0])).toBe(0);
|
||||
expect(dpRainTerraces([0, 1, 0, 0])).toBe(0);
|
||||
expect(dpRainTerraces([0, 1, 0, 0, 1, 0])).toBe(2);
|
||||
expect(dpRainTerraces([0, 2, 0, 0, 1, 0])).toBe(2);
|
||||
expect(dpRainTerraces([2, 0, 2])).toBe(2);
|
||||
expect(dpRainTerraces([2, 0, 5])).toBe(2);
|
||||
expect(dpRainTerraces([3, 0, 0, 2, 0, 4])).toBe(10);
|
||||
expect(dpRainTerraces([0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1])).toBe(6);
|
||||
expect(dpRainTerraces([1, 1, 1, 1, 1])).toBe(0);
|
||||
expect(dpRainTerraces([1, 2, 3, 4, 5])).toBe(0);
|
||||
expect(dpRainTerraces([4, 1, 3, 1, 2, 1, 2, 1])).toBe(4);
|
||||
expect(dpRainTerraces([0, 2, 4, 3, 4, 2, 4, 0, 8, 7, 0])).toBe(7);
|
||||
});
|
||||
});
|
||||
@ -1,21 +0,0 @@
|
||||
import rainTerraces from '../rainTerraces';
|
||||
|
||||
describe('rainTerraces', () => {
|
||||
it('should find the amount of water collected after raining', () => {
|
||||
expect(rainTerraces([1])).toBe(0);
|
||||
expect(rainTerraces([1, 0])).toBe(0);
|
||||
expect(rainTerraces([0, 1])).toBe(0);
|
||||
expect(rainTerraces([0, 1, 0])).toBe(0);
|
||||
expect(rainTerraces([0, 1, 0, 0])).toBe(0);
|
||||
expect(rainTerraces([0, 1, 0, 0, 1, 0])).toBe(2);
|
||||
expect(rainTerraces([0, 2, 0, 0, 1, 0])).toBe(2);
|
||||
expect(rainTerraces([2, 0, 2])).toBe(2);
|
||||
expect(rainTerraces([2, 0, 5])).toBe(2);
|
||||
expect(rainTerraces([3, 0, 0, 2, 0, 4])).toBe(10);
|
||||
expect(rainTerraces([0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1])).toBe(6);
|
||||
expect(rainTerraces([1, 1, 1, 1, 1])).toBe(0);
|
||||
expect(rainTerraces([1, 2, 3, 4, 5])).toBe(0);
|
||||
expect(rainTerraces([4, 1, 3, 1, 2, 1, 2, 1])).toBe(4);
|
||||
expect(rainTerraces([0, 2, 4, 3, 4, 2, 4, 0, 8, 7, 0])).toBe(7);
|
||||
});
|
||||
});
|
||||
33
src/algorithms/uncategorized/rain-terraces/bfRainTerraces.js
Normal file
33
src/algorithms/uncategorized/rain-terraces/bfRainTerraces.js
Normal file
@ -0,0 +1,33 @@
|
||||
/**
|
||||
* BRUTE FORCE approach of solving Trapping Rain Water problem.
|
||||
*
|
||||
* @param {number[]} terraces
|
||||
* @return {number}
|
||||
*/
|
||||
export default function bfRainTerraces(terraces) {
|
||||
let waterAmount = 0;
|
||||
|
||||
for (let terraceIndex = 0; terraceIndex < terraces.length; terraceIndex += 1) {
|
||||
// Get left most high terrace.
|
||||
let leftHighestLevel = 0;
|
||||
for (let leftIndex = terraceIndex - 1; leftIndex >= 0; leftIndex -= 1) {
|
||||
leftHighestLevel = Math.max(leftHighestLevel, terraces[leftIndex]);
|
||||
}
|
||||
|
||||
// Get right most high terrace.
|
||||
let rightHighestLevel = 0;
|
||||
for (let rightIndex = terraceIndex + 1; rightIndex < terraces.length; rightIndex += 1) {
|
||||
rightHighestLevel = Math.max(rightHighestLevel, terraces[rightIndex]);
|
||||
}
|
||||
|
||||
// Add current terrace water amount.
|
||||
const terraceBoundaryLevel = Math.min(leftHighestLevel, rightHighestLevel);
|
||||
if (terraceBoundaryLevel > terraces[terraceIndex]) {
|
||||
// Terrace will be able to store the water if the lowest of two left and right highest
|
||||
// terraces are still higher than the current one.
|
||||
waterAmount += Math.min(leftHighestLevel, rightHighestLevel) - terraces[terraceIndex];
|
||||
}
|
||||
}
|
||||
|
||||
return waterAmount;
|
||||
}
|
||||
@ -1,8 +1,10 @@
|
||||
/**
|
||||
* DYNAMIC PROGRAMMING approach of solving Trapping Rain Water problem.
|
||||
*
|
||||
* @param {number[]} terraces
|
||||
* @return {number}
|
||||
*/
|
||||
export default function rainTerraces(terraces) {
|
||||
export default function dpRainTerraces(terraces) {
|
||||
/*
|
||||
* STEPS
|
||||
*
|
||||
Loading…
Reference in New Issue
Block a user