hxx/javascript-algorithms
1
0
Fork 0
mirror of https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git synced 2024-12-27 15:41:16 +08:00
Code Issues Packages Projects Releases Wiki Activity

Refactor segment tree implementation.

Browse Source
This commit is contained in:
Oleksii Trekhleb 2018-06-05 08:45:00 +03:00
parent 5784a4a95b
commit 434a5649cb
4 changed files with 234 additions and 252 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

1
README.md
View File

@ -32,6 +32,7 @@ the data.
* [Binary Search Tree](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/tree/binary-search-tree) * [Binary Search Tree](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/tree/binary-search-tree)
* [AVL Tree](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/tree/avl-tree) * [AVL Tree](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/tree/avl-tree)
* [Red-Black Tree](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/tree/red-black-tree) * [Red-Black Tree](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/tree/red-black-tree)
* [Segment Tree](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/tree/segment-tree) - with min/max/sum range queries examples
* [Graph](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/graph) (both directed and undirected) * [Graph](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/graph) (both directed and undirected)
* [Disjoint Set](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/disjoint-set) * [Disjoint Set](https://github.com/trekhleb/javascript-algorithms/tree/master/src/data-structures/disjoint-set)

55
src/data-structures/tree/segment-tree/README.md
View File

@ -1,41 +1,23 @@
# Segment Tree # Segment Tree
A segment tree is a data structure designed to perform In computer science, a segment tree also known as a statistic tree
certain array operations efficiently - especially those is a tree data structure used for storing information about intervals,
involving range queries. or segments. It allows querying which of the stored segments contain
a given point. It is, in principle, a static structure; that is,
it's a structure that cannot be modified once it's built. A similar
data structure is the interval tree.
A common application is the [Range Minimum Query](https://en.wikipedia.org/wiki/Range_minimum_query) (RMQ) problem, A segment tree is a binary tree. The root of the tree represents the
where we are given an array of numbers and need to
support operations of updating values of the array and
finding the minimum of a contiguous subarray.
A segment tree implementation for the RMQ problem
takes `O(n)` to initialize, and `O(log n)` per query or
update. The "minimum" operation can be replaced by any
array operation (such as sum).
A segment tree is a binary tree with contiguous
sub-arrays as nodes. The root of the tree represents the
whole array. The two children of the root represent the whole array. The two children of the root represent the
first and second halves of the array. Similarly, the first and second halves of the array. Similarly, the
children of each node corresponds to the two halves of children of each node corresponds to the two halves of
the array corresponding to the node. If the array has the array corresponding to the node.
size `n`, we can prove that the segment tree has size at
most `4n`. Each node stores the minimum of its
corresponding sub-array.
In the implementation, we do not explicitly store this
tree structure, but represent it using a `4n` sized array.
The left child of node i is `2i+1` and the right child
is `2i+2`. This is a standard way to represent segment
trees, and lends itself to an efficient implementation.
We build the tree bottom up, with the value of each node We build the tree bottom up, with the value of each node
being the minimum of its children's values. This will being the "minimum" (or any other function) of its children's values. This will
take time `O(n)`, with one operation for each node. Updates take `O(n log n)` time. The number
are also done bottom up, with values being recomputed
starting from the leaf, and up to the root. The number
of operations done is the height of the tree, which of operations done is the height of the tree, which
is `O(log n)`. To answer queries, each node splits the is `O(log n)`. To do range queries, each node splits the
query into two parts, one sub-query for each child. query into two parts, one sub-query for each child.
If a query contains the whole subarray of a node, we If a query contains the whole subarray of a node, we
can use the precomputed value at the node. Using this can use the precomputed value at the node. Using this
@ -44,6 +26,21 @@ operations are done.
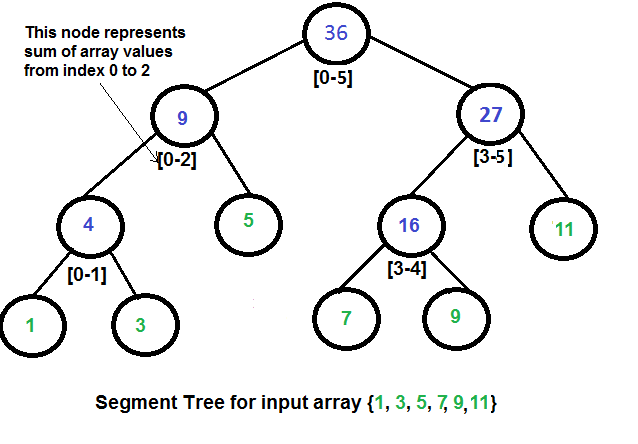
![Segment Tree](https://www.geeksforgeeks.org/wp-content/uploads/segment-tree1.png) ![Segment Tree](https://www.geeksforgeeks.org/wp-content/uploads/segment-tree1.png)
## Application
A segment tree is a data structure designed to perform
certain array operations efficiently - especially those
involving range queries.
Applications of the segment tree are in the areas of computational geometry,
and geographic information systems.
Current implementation of Segment Tree implies that you may
pass any binary (with two input params) function to it and
thus you're able to do range query for variety of functions.
In tests you may fins examples of doing `min`, `max` and `sam` range
queries on SegmentTree.
## References ## References
- [Wikipedia](https://en.wikipedia.org/wiki/Segment_tree) - [Wikipedia](https://en.wikipedia.org/wiki/Segment_tree)

245
src/data-structures/tree/segment-tree/SegmentTree.js
View File

@ -1,149 +1,168 @@
/** import isPowerOfTwo from '../../../algorithms/math/is-power-of-two/isPowerOfTwo';
* Segment Tree implementation for Range Query data structure
* Tracks a array of numbers. 0 indexed
* operation is a binary function (eg sum, min) - needs to be associative
* identity is the identity of the operation
* i.e, operation(x, identity) = x (eg 0 for sum, Infinity for min)
* Supports methods
* update(index, val) - set value of index
* query(l, r) - finds operation(values in range [l, r]) (both inclusive)
*
* As is customary, we store the tree implicitly with i being the parent of 2i, 2i+1.
*/
export default class SegmentTree { export default class SegmentTree {
/** /**
* array initialises the numbers * @param {number[]} inputArray
* @param {number[]} array * @param {function} operation - binary function (i.e. sum, min)
* @param {number} operationFallback - operation fallback value (i.e. 0 for sum, Infinity for min)
*/ */
constructor(array, operation, identity) { constructor(inputArray, operation, operationFallback) {
this.n = array.length; this.inputArray = inputArray;
this.array = array;
this.tree = new Array(4 * this.n);
this.operation = operation; this.operation = operation;
this.identity = identity; this.operationFallback = operationFallback;
// use Range Min Query by default // Init array representation of segment tree.
if (this.operation === undefined) { this.segmentTree = this.initSegmentTree(this.inputArray);
this.operation = Math.min;
this.identity = Infinity;
}
this.buildSegmentTree();
this.build();
} }
/** /**
* Stub for recursive call * @param {number[]} inputArray
* @return {number[]}
*/ */
build() { initSegmentTree(inputArray) {
this.buildRec(1, 0, this.n - 1); let segmentTreeArrayLength;
} const inputArrayLength = inputArray.length;
/** if (isPowerOfTwo(inputArrayLength)) {
* Left child index // If original array length is a power of two.
* @param {number} root segmentTreeArrayLength = (2 * inputArrayLength) - 1;
*/
left(root) {
return 2 * root;
}
/**
* Right child index
* @param {number} root
*/
right(root) {
return (2 * root) + 1;
}
/**
* root is the index in the tree, [l,r] (inclusive) is the current array segment being built
* @param {number} root
* @param {number} l
* @param {number} r
*/
buildRec(root, l, r) {
if (l === r) {
this.tree[root] = this.array[l];
} else { } else {
const mid = Math.floor((l + r) / 2); // If original array length is not a power of two then we need to find
// build left and right nodes // next number that is a power of two and use it to calculate
this.buildRec(this.left(root), l, mid); // tree array size. This is happens because we need to fill empty children
this.buildRec(this.right(root), mid + 1, r); // in perfect binary tree with nulls.And those nulls need extra space.
this.tree[root] = this.operation(this.tree[this.left(root)], this.tree[this.right(root)]); const currentPower = Math.floor(Math.log2(inputArrayLength));
const nextPower = currentPower + 1;
const nextPowerOfTwoNumber = 2 ** nextPower;
segmentTreeArrayLength = (2 * nextPowerOfTwoNumber) - 1;
} }
return new Array(segmentTreeArrayLength).fill(null);
} }
/** /**
* Stub for recursive call * Build segment tree.
* @param {number} lindex
* @param {number} rindex
*/ */
query(lindex, rindex) { buildSegmentTree() {
return this.queryRec(1, lindex, rindex, 0, this.n - 1); const leftIndex = 0;
const rightIndex = this.inputArray.length - 1;
const position = 0;
this.buildTreeRecursively(leftIndex, rightIndex, position);
} }
/** /**
* [lindex, rindex] is the query region * Build segment tree recursively.
* [l,r] is the current region being processed *
* Guaranteed that [lindex,rindex] contained in [l,r] * @param {number} leftInputIndex
* @param {number} root * @param {number} rightInputIndex
* @param {number} lindex * @param {number} position
* @param {number} rindex
* @param {number} l
* @param {number} r
*/ */
queryRec(root, lindex, rindex, l, r) { buildTreeRecursively(leftInputIndex, rightInputIndex, position) {
// console.log(root, lindex, rindex, l, r); // If low input index and high input index are equal that would mean
if (lindex > rindex) { // the we have finished splitting and we are already came to the leaf
// happens when mid+1 > r - no segment // of the segment tree. We need to copy this leaf value from input
return this.identity; // array to segment tree.
if (leftInputIndex === rightInputIndex) {
this.segmentTree[position] = this.inputArray[leftInputIndex];
return;
} }
if (l === lindex && r === rindex) {
// query region matches current region - use tree value // Split input array on two halves and process them recursively.
return this.tree[root]; const middleIndex = Math.floor((leftInputIndex + rightInputIndex) / 2);
} // Process left half of the input array.
const mid = Math.floor((l + r) / 2); this.buildTreeRecursively(leftInputIndex, middleIndex, this.getLeftChildIndex(position));
// get left and right results and combine // Process right half of the input array.
const leftResult = this.queryRec(this.left(root), lindex, Math.min(rindex, mid), l, mid); this.buildTreeRecursively(middleIndex + 1, rightInputIndex, this.getRightChildIndex(position));
const rightResult = this.queryRec(
this.right(root), Math.max(mid + 1, lindex), rindex, // Once every tree leaf is not empty we're able to build tree bottom up using
mid + 1, r, // provided operation function.
this.segmentTree[position] = this.operation(
this.segmentTree[this.getLeftChildIndex(position)],
this.segmentTree[this.getRightChildIndex(position)],
); );
return this.operation(leftResult, rightResult);
} }
/** /**
* Set array[index] to value * Do range query on segment tree in context of this.operation function.
* @param {number} index *
* @param {number} value * @param {number} queryLeftIndex
* @param {number} queryRightIndex
* @return {number}
*/ */
update(index, value) { rangeQuery(queryLeftIndex, queryRightIndex) {
this.array[index] = value; const leftIndex = 0;
this.updateRec(1, index, value, 0, this.n - 1); const rightIndex = this.inputArray.length - 1;
const position = 0;
return this.rangeQueryRecursive(
queryLeftIndex,
queryRightIndex,
leftIndex,
rightIndex,
position,
);
} }
/** /**
* @param {number} root * Do range query on segment tree recursively in context of this.operation function.
* @param {number} index *
* @param {number} value * @param {number} queryLeftIndex - left index of the query
* @param {number} l * @param {number} queryRightIndex - right index of the query
* @param {number} r * @param {number} leftIndex - left index of input array segment
* @param {number} rightIndex - right index of input array segment
* @param {number} position - root position in binary tree
* @return {number}
*/ */
updateRec(root, index, value, l, r) { rangeQueryRecursive(queryLeftIndex, queryRightIndex, leftIndex, rightIndex, position) {
if (l === r) { if (queryLeftIndex <= leftIndex && queryRightIndex >= rightIndex) {
// we are at tree node containing array[index] // Total overlap.
this.tree[root] = value; return this.segmentTree[position];
} else {
const mid = Math.floor((l + r) / 2);
// update whichever child index is in, update this.tree[root]
if (index <= mid) {
this.updateRec(this.left(root), index, value, l, mid);
} else {
this.updateRec(this.right(root), index, value, mid + 1, r);
} }
this.tree[root] = this.operation(this.tree[this.left(root)], this.tree[this.right(root)]);
if (queryLeftIndex > rightIndex || queryRightIndex < leftIndex) {
// No overlap.
return this.operationFallback;
} }
// Partial overlap.
const middleIndex = Math.floor((leftIndex + rightIndex) / 2);
const leftOperationResult = this.rangeQueryRecursive(
queryLeftIndex,
queryRightIndex,
leftIndex,
middleIndex,
this.getLeftChildIndex(position),
);
const rightOperationResult = this.rangeQueryRecursive(
queryLeftIndex,
queryRightIndex,
middleIndex + 1,
rightIndex,
this.getRightChildIndex(position),
);
return this.operation(leftOperationResult, rightOperationResult);
}
/**
* Left child index.
* @param {number} parentIndex
* @return {number}
*/
getLeftChildIndex(parentIndex) {
return (2 * parentIndex) + 1;
}
/**
* Right child index.
* @param {number} parentIndex
* @return {number}
*/
getRightChildIndex(parentIndex) {
return (2 * parentIndex) + 2;
} }
} }

183
src/data-structures/tree/segment-tree/__test__/SegmentTree.test.js
View File

@ -1,136 +1,101 @@
import SegmentTree from '../SegmentTree'; import SegmentTree from '../SegmentTree';
describe('SegmentTree', () => { describe('SegmentTree', () => {
it('create RMQ SegmentTree', () => { it('should build tree for input array #0 with length of power of two', () => {
const array = [1, 2, 5, 3, 4, 6, 2]; const array = [-1, 2];
const segTree = new SegmentTree(array, Math.min, Infinity); const segmentTree = new SegmentTree(array, Math.min, Infinity);
expect(segTree.array.sort()).toEqual(array.sort()); expect(segmentTree.segmentTree).toEqual([-1, -1, 2]);
expect(segTree.n).toBe(7); expect(segmentTree.segmentTree.length).toBe((2 * array.length) - 1);
}); });
it('check specific tree indices', () => { it('should build tree for input array #1 with length of power of two', () => {
const array = [1, 2, 5, 3, 4, 6, 2]; const array = [-1, 2, 4, 0];
const segTree = new SegmentTree(array, Math.min, Infinity); const segmentTree = new SegmentTree(array, Math.min, Infinity);
// 1 - [0,6] expect(segmentTree.segmentTree).toEqual([-1, -1, 0, -1, 2, 4, 0]);
// 2 - [0,3] 3 - [4,6] expect(segmentTree.segmentTree.length).toBe((2 * array.length) - 1);
// 4 - [0,1] 5 - [2,3] 6 - [4,5] 7 - [6,6]
// 8 - [0,0] 9 - [1,1] 10 - [2,2] 11 - [3,3] 12 - [4,4] 13 - [5,5]
expect(segTree.tree.slice(8, 14)).toEqual(array.slice(0, 6));
expect(segTree.tree[7]).toBe(array[6]);
expect(segTree.tree[1]).toBe(Math.min(...array));
expect(segTree.tree[2]).toBe(Math.min(...array.slice(0, 4)));
expect(segTree.tree[6]).toBe(Math.min(...array.slice(4, 6)));
}); });
it('check another tree for n=8', () => { it('should build tree for input array #0 with length not of power of two', () => {
const array = [5, 4, 2, 1, 4, 1, 3, 1]; const array = [0, 1, 2];
const segTree = new SegmentTree(array, Math.min, Infinity); const segmentTree = new SegmentTree(array, Math.min, Infinity);
// 1 - [0,7] expect(segmentTree.segmentTree).toEqual([0, 0, 2, 0, 1, null, null]);
// 2 - [0,3] 3 - [4,7] expect(segmentTree.segmentTree.length).toBe((2 * 4) - 1);
// 4 - [0,1] 5 - [2,3] 6 - [4,5] 7 - [6,7]
// 8 - [0,0] 9 - [1,1] 10 - [2,2] 11 - [3,3] 12 - [4,4] 13 - [5,5] 14 - [6,6] 15 - [7,7]
expect(segTree.tree.slice(8, 16)).toEqual(array.slice(0, 8));
expect(segTree.tree[7]).toBe(Math.min(...array.slice(6, 8)));
expect(segTree.tree[1]).toBe(Math.min(...array));
expect(segTree.tree[2]).toBe(Math.min(...array.slice(0, 4)));
expect(segTree.tree[6]).toBe(Math.min(...array.slice(4, 6)));
}); });
it('check query', () => { it('should build tree for input array #1 with length not of power of two', () => {
const array = [1, 2, 5, 3, 4, 6, 2]; const array = [-1, 3, 4, 0, 2, 1];
const segTree = new SegmentTree(array, Math.min, Infinity); const segmentTree = new SegmentTree(array, Math.min, Infinity);
const testRanges = [[0, 6], [0, 4], [2, 6], [3, 3], [4, 5], [6, 6], [1, 5], [1, 4]]; expect(segmentTree.segmentTree).toEqual([
for (let i = 0; i < testRanges.length; i += 1) { -1, -1, 0, -1, 4, 0, 1, -1, 3, null, null, 0, 2, null, null,
const range = testRanges[i]; ]);
expect(segTree.query(range[0], range[1])) expect(segmentTree.segmentTree.length).toBe((2 * 8) - 1);
.toBe(Math.min(...array.slice(range[0], range[1] + 1)));
}
expect(segTree.query(0, 0)).toBe(1);
}); });
it('check update using queries', () => { it('should build max array', () => {
const array = [1, 2, 5, 3, 4, 6, 2]; const array = [-1, 2, 4, 0];
const segTree = new SegmentTree(array, Math.min, Infinity); const segmentTree = new SegmentTree(array, Math.max, -Infinity);
const testRanges = [[0, 6], [0, 4], [2, 6], [3, 3], [4, 5], [6, 6], [1, 5], [1, 4]]; expect(segmentTree.segmentTree).toEqual([4, 2, 4, -1, 2, 4, 0]);
expect(segmentTree.segmentTree.length).toBe((2 * array.length) - 1);
expect(segTree.array[0]).toBe(1);
for (let i = 0; i < testRanges.length; i += 1) {
const range = testRanges[i];
expect(segTree.query(range[0], range[1]))
.toBe(Math.min(...array.slice(range[0], range[1] + 1)));
}
segTree.update(0, 3);
array[0] = 3;
expect(segTree.array[0]).toBe(3);
for (let i = 0; i < testRanges.length; i += 1) {
const range = testRanges[i];
expect(segTree.query(range[0], range[1]))
.toBe(Math.min(...array.slice(range[0], range[1] + 1)));
}
segTree.update(2, 2);
array[2] = 2;
expect(segTree.array[2]).toBe(2);
for (let i = 0; i < testRanges.length; i += 1) {
const range = testRanges[i];
expect(segTree.query(range[0], range[1]))
.toBe(Math.min(...array.slice(range[0], range[1] + 1)));
}
}); });
it('check range sum query SegmentTree', () => { it('should build sum array', () => {
const array = [1, 2, 5, 3, 4, 6, 2]; const array = [-1, 2, 4, 0];
const sum = (a, b) => a + b; const segmentTree = new SegmentTree(array, (a, b) => (a + b), 0);
const segTree = new SegmentTree(array, sum, 0);
const testRanges = [[0, 6], [0, 4], [2, 6], [3, 3], [4, 5], [6, 6], [1, 5], [1, 4]]; expect(segmentTree.segmentTree).toEqual([5, 1, 4, -1, 2, 4, 0]);
expect(segmentTree.segmentTree.length).toBe((2 * array.length) - 1);
expect(segTree.array[0]).toBe(1);
for (let i = 0; i < testRanges.length; i += 1) {
const range = testRanges[i];
expect(segTree.query(range[0], range[1]))
.toBe(array.slice(range[0], range[1] + 1).reduce(sum));
}
segTree.update(0, 3);
array[0] = 3;
expect(segTree.array[0]).toBe(3);
for (let i = 0; i < testRanges.length; i += 1) {
const range = testRanges[i];
expect(segTree.query(range[0], range[1]))
.toBe(array.slice(range[0], range[1] + 1).reduce(sum));
}
}); });
it('check default is rmq', () => { it('should do min range query on power of two length array', () => {
const array = [3, 7, 2, 5, 4, 3, 8, 1]; const array = [-1, 3, 4, 0, 2, 1];
const segTree = new SegmentTree(array); const segmentTree = new SegmentTree(array, Math.min, Infinity);
const testRanges = [[0, 7], [3, 7], [2, 5], [4, 4]]; expect(segmentTree.rangeQuery(0, 5)).toBe(-1);
expect(segmentTree.rangeQuery(0, 2)).toBe(-1);
expect(segmentTree.rangeQuery(1, 3)).toBe(0);
expect(segmentTree.rangeQuery(2, 4)).toBe(0);
expect(segmentTree.rangeQuery(4, 5)).toBe(1);
expect(segmentTree.rangeQuery(2, 2)).toBe(4);
});
for (let i = 0; i < testRanges.length; i += 1) { it('should do min range query on not power of two length array', () => {
const range = testRanges[i]; const array = [-1, 2, 4, 0];
expect(segTree.query(range[0], range[1])) const segmentTree = new SegmentTree(array, Math.min, Infinity);
.toBe(Math.min(...array.slice(range[0], range[1] + 1)));
}
segTree.update(0, 1); expect(segmentTree.rangeQuery(0, 4)).toBe(-1);
array[0] = 1; expect(segmentTree.rangeQuery(0, 1)).toBe(-1);
expect(segmentTree.rangeQuery(1, 3)).toBe(0);
expect(segmentTree.rangeQuery(1, 2)).toBe(2);
expect(segmentTree.rangeQuery(2, 3)).toBe(0);
expect(segmentTree.rangeQuery(2, 2)).toBe(4);
});
expect(segTree.array[0]).toBe(1); it('should do max range query', () => {
for (let i = 0; i < testRanges.length; i += 1) { const array = [-1, 3, 4, 0, 2, 1];
const range = testRanges[i]; const segmentTree = new SegmentTree(array, Math.max, -Infinity);
expect(segTree.query(range[0], range[1]))
.toBe(Math.min(...array.slice(range[0], range[1] + 1))); expect(segmentTree.rangeQuery(0, 5)).toBe(4);
} expect(segmentTree.rangeQuery(0, 1)).toBe(3);
expect(segmentTree.rangeQuery(1, 3)).toBe(4);
expect(segmentTree.rangeQuery(2, 4)).toBe(4);
expect(segmentTree.rangeQuery(4, 5)).toBe(2);
expect(segmentTree.rangeQuery(3, 3)).toBe(0);
});
it('should do sum range query', () => {
const array = [-1, 3, 4, 0, 2, 1];
const segmentTree = new SegmentTree(array, (a, b) => (a + b), 0);
expect(segmentTree.rangeQuery(0, 5)).toBe(9);
expect(segmentTree.rangeQuery(0, 1)).toBe(2);
expect(segmentTree.rangeQuery(1, 3)).toBe(7);
expect(segmentTree.rangeQuery(2, 4)).toBe(6);
expect(segmentTree.rangeQuery(4, 5)).toBe(3);
expect(segmentTree.rangeQuery(3, 3)).toBe(0);
}); });
}); });