mirror of
https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git
synced 2024-12-25 22:46:20 +08:00
Add Tower of Hanoi.
This commit is contained in:
parent
26ba21b34c
commit
44b0a99a80
@ -77,6 +77,7 @@
|
||||
* [Eulerian Path and Eulerian Circuit](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/eulerian-path) - Fleury's algorithm
|
||||
* [Strongly Connected Components](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/strongly-connected-components) - Kosaraju's algorithm
|
||||
* **Uncategorized**
|
||||
* [Tower of Hanoi](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/uncategorized/hanoi-tower)
|
||||
* Union-Find
|
||||
* Maze
|
||||
* Sudoku
|
||||
@ -89,6 +90,7 @@
|
||||
* [Prim’s Algorithm](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/prim) - finding Minimum Spanning Tree (MST) for weighted undirected graph
|
||||
* [Kruskal’s Algorithm](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/kruskal) - finding Minimum Spanning Tree (MST) for weighted undirected graph
|
||||
* **Divide and Conquer**
|
||||
* [Tower of Hanoi](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/uncategorized/hanoi-tower)
|
||||
* [Euclidean Algorithm](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/euclidean-algorithm) - calculate the Greatest Common Divisor (GCD)
|
||||
* [Permutations](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/permutations) (with and without repetitions)
|
||||
* [Combinations](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sets/combinations) (with and without repetitions)
|
||||
|
||||
29
src/algorithms/uncategorized/hanoi-tower/README.md
Normal file
29
src/algorithms/uncategorized/hanoi-tower/README.md
Normal file
@ -0,0 +1,29 @@
|
||||
# Tower of Hanoi
|
||||
|
||||
The Tower of Hanoi (also called the Tower of Brahma or Lucas'
|
||||
Tower and sometimes pluralized) is a mathematical game or puzzle.
|
||||
It consists of three rods and a number of disks of different sizes,
|
||||
which can slide onto any rod. The puzzle starts with the disks in
|
||||
a neat stack in ascending order of size on one rod, the smallest
|
||||
at the top, thus making a conical shape.
|
||||
|
||||
The objective of the puzzle is to move the entire stack to another
|
||||
rod, obeying the following simple rules:
|
||||
|
||||
- Only one disk can be moved at a time.
|
||||
- Each move consists of taking the upper disk from one of the
|
||||
stacks and placing it on top of another stack or on an empty rod.
|
||||
- No disk may be placed on top of a smaller disk.
|
||||
|
||||
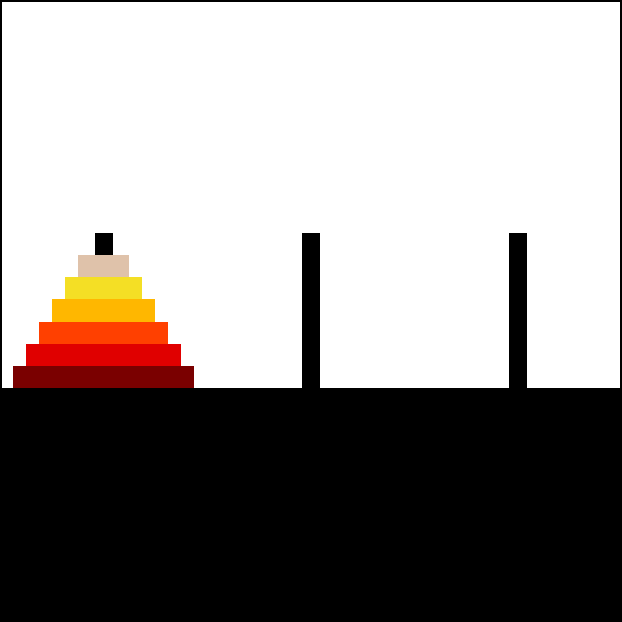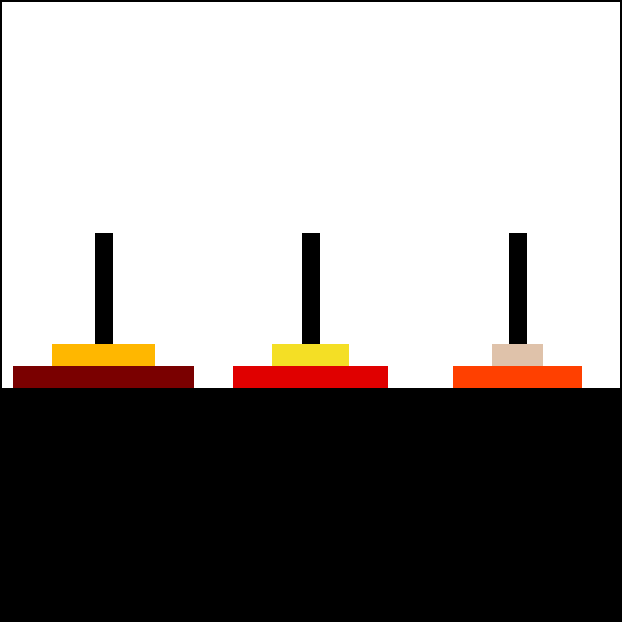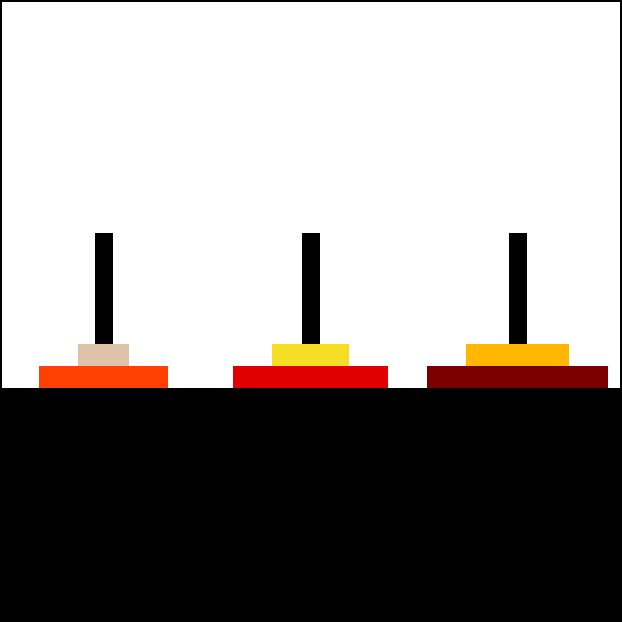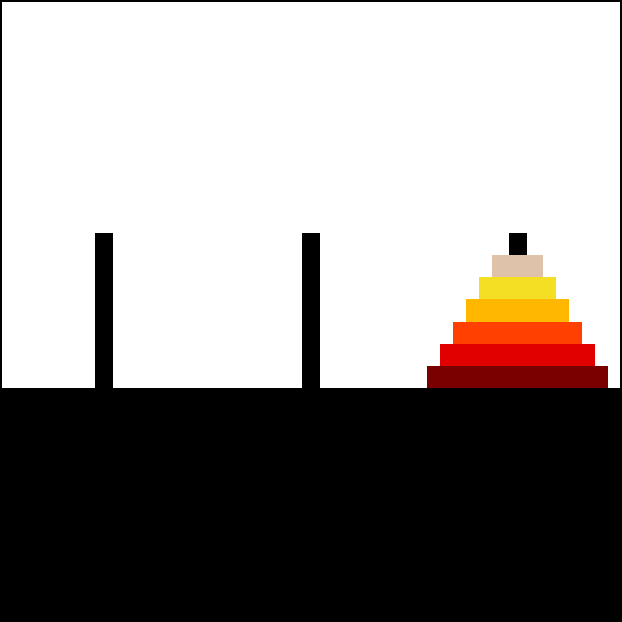
|
||||
|
||||
Animation of an iterative algorithm solving 6-disk problem
|
||||
|
||||
With `3` disks, the puzzle can be solved in `7` moves. The minimal
|
||||
number of moves required to solve a Tower of Hanoi puzzle
|
||||
is `2n − 1`, where `n` is the number of disks.
|
||||
|
||||
## References
|
||||
|
||||
- [Wikipedia](https://en.wikipedia.org/wiki/Tower_of_Hanoi)
|
||||
- [HackerEarth](https://www.hackerearth.com/blog/algorithms/tower-hanoi-recursion-game-algorithm-explained/)
|
||||
@ -0,0 +1,39 @@
|
||||
import hanoiTower from '../hanoiTower';
|
||||
|
||||
describe('hanoiTower', () => {
|
||||
it('should solve tower of hanoi puzzle with 2 discs', () => {
|
||||
const moveCallbackMock = jest.fn();
|
||||
|
||||
hanoiTower(2, moveCallbackMock);
|
||||
|
||||
expect(moveCallbackMock).toHaveBeenCalledTimes(3);
|
||||
|
||||
expect(moveCallbackMock.mock.calls[0][0]).toBe(1);
|
||||
expect(moveCallbackMock.mock.calls[0][1]).toEqual([1, 2]);
|
||||
expect(moveCallbackMock.mock.calls[0][2]).toEqual([]);
|
||||
|
||||
expect(moveCallbackMock.mock.calls[1][0]).toBe(2);
|
||||
expect(moveCallbackMock.mock.calls[1][1]).toEqual([2]);
|
||||
expect(moveCallbackMock.mock.calls[1][2]).toEqual([]);
|
||||
|
||||
expect(moveCallbackMock.mock.calls[2][0]).toBe(1);
|
||||
expect(moveCallbackMock.mock.calls[2][1]).toEqual([1]);
|
||||
expect(moveCallbackMock.mock.calls[2][2]).toEqual([2]);
|
||||
});
|
||||
|
||||
it('should solve tower of hanoi puzzle with 3 discs', () => {
|
||||
const moveCallbackMock = jest.fn();
|
||||
|
||||
hanoiTower(3, moveCallbackMock);
|
||||
|
||||
expect(moveCallbackMock).toHaveBeenCalledTimes(7);
|
||||
});
|
||||
|
||||
it('should solve tower of hanoi puzzle with 6 discs', () => {
|
||||
const moveCallbackMock = jest.fn();
|
||||
|
||||
hanoiTower(6, moveCallbackMock);
|
||||
|
||||
expect(moveCallbackMock).toHaveBeenCalledTimes(63);
|
||||
});
|
||||
});
|
||||
94
src/algorithms/uncategorized/hanoi-tower/hanoiTower.js
Normal file
94
src/algorithms/uncategorized/hanoi-tower/hanoiTower.js
Normal file
@ -0,0 +1,94 @@
|
||||
import Stack from '../../../data-structures/stack/Stack';
|
||||
|
||||
/**
|
||||
* @param {Stack} fromPole
|
||||
* @param {Stack} toPole
|
||||
* @param {function(disc: number, fromPole: number[], toPole: number[])} moveCallback
|
||||
*/
|
||||
function moveDisc(fromPole, toPole, moveCallback) {
|
||||
moveCallback(fromPole.peek(), fromPole.toArray(), toPole.toArray());
|
||||
|
||||
const disc = fromPole.pop();
|
||||
toPole.push(disc);
|
||||
}
|
||||
|
||||
/**
|
||||
* @param {number} numberOfDiscs
|
||||
* @param {Stack} fromPole
|
||||
* @param {Stack} withPole
|
||||
* @param {Stack} toPole
|
||||
* @param {function(disc: number, fromPole: number[], toPole: number[])} moveCallback
|
||||
*/
|
||||
function hanoiTowerRecursive({
|
||||
numberOfDiscs,
|
||||
fromPole,
|
||||
withPole,
|
||||
toPole,
|
||||
moveCallback,
|
||||
}) {
|
||||
if (numberOfDiscs === 1) {
|
||||
// Base case with just one disc.
|
||||
moveDisc(fromPole, toPole, moveCallback);
|
||||
} else {
|
||||
// In case if there are more discs then move them recursively.
|
||||
|
||||
// Expose the bottom disc on fromPole stack.
|
||||
hanoiTowerRecursive({
|
||||
numberOfDiscs: numberOfDiscs - 1,
|
||||
fromPole,
|
||||
withPole: toPole,
|
||||
toPole: withPole,
|
||||
moveCallback,
|
||||
});
|
||||
|
||||
// Move the disc that was exposed to its final destination.
|
||||
hanoiTowerRecursive({
|
||||
numberOfDiscs: 1,
|
||||
fromPole,
|
||||
withPole,
|
||||
toPole,
|
||||
moveCallback,
|
||||
});
|
||||
|
||||
// Move temporary tower from auxiliary pole to its final destination.
|
||||
hanoiTowerRecursive({
|
||||
numberOfDiscs: numberOfDiscs - 1,
|
||||
fromPole: withPole,
|
||||
withPole: fromPole,
|
||||
toPole,
|
||||
moveCallback,
|
||||
});
|
||||
}
|
||||
}
|
||||
|
||||
/**
|
||||
* @param {number} numberOfDiscs
|
||||
* @param {function(disc: number, fromPole: number[], toPole: number[])} moveCallback
|
||||
*/
|
||||
export default function hanoiTower(numberOfDiscs, moveCallback) {
|
||||
// Each of three poles of Tower of Hanoi puzzle is represented as a stack
|
||||
// that might contain elements (discs). Each disc is represented as a number.
|
||||
// Larger discs have bigger number equivalent.
|
||||
|
||||
// The pole from where the discs should be moved.
|
||||
const fromPole = new Stack();
|
||||
|
||||
// The middle pole that should be used as a helper.
|
||||
const withPole = new Stack();
|
||||
|
||||
// The destination pole where all discs need to be moved.
|
||||
const toPole = new Stack();
|
||||
|
||||
// Let's create the discs and put them to the fromPole.
|
||||
for (let discSize = numberOfDiscs; discSize > 0; discSize -= 1) {
|
||||
fromPole.push(discSize);
|
||||
}
|
||||
|
||||
hanoiTowerRecursive({
|
||||
numberOfDiscs,
|
||||
fromPole,
|
||||
withPole,
|
||||
toPole,
|
||||
moveCallback,
|
||||
});
|
||||
}
|
||||
@ -13,7 +13,7 @@ export default class Stack {
|
||||
}
|
||||
|
||||
/**
|
||||
* @return {LinkedListNode}
|
||||
* @return {*}
|
||||
*/
|
||||
peek() {
|
||||
if (!this.linkedList.tail) {
|
||||
|
||||
Loading…
Reference in New Issue
Block a user