Merge branch 'master' into fibonacci

2024-11-10 11:09:43 +08:00 · 2019-04-19 18:08:21 +05:30 · 2019-04-19 18:08:21 +05:30 · 44bf05da8e
commit 44bf05da8e
parent 8a73675814 94abfec91d
77 changed files with 6667 additions and 2892 deletions
--- a/.babelrc
+++ b/.babelrc
@ -1,3 +1,3 @@
 {
-  "presets": ["env"]
+  "presets": ["@babel/preset-env"]
 }
--- a/.huskyrc.json
+++ b/.huskyrc.json
@ -0,0 +1,5 @@
+{
+  "hooks": {
+    "pre-commit": "npm run lint && npm run test"
+  }
+}
--- a/.travis.yml
+++ b/.travis.yml
@ -2,7 +2,7 @@ sudo: required
 dist: trusty
 language: node_js
 node_js:
-  - node
+  - "11"
 install:
  - npm install -g codecov
  - npm install
--- a/README.ja-JP.md
+++ b/README.ja-JP.md
@ -3,11 +3,11 @@
 [![Build Status](https://travis-ci.org/trekhleb/javascript-algorithms.svg?branch=master)](https://travis-ci.org/trekhleb/javascript-algorithms)
 [![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)

-このリポジトリには、JavaScriptベースの多数のサンプル
-一般的なアルゴリズムとデータ構造。
+このリポジトリには、JavaScriptベースの一般的なアルゴリズムとデータ構造に関する多数のサンプルが含まれています。

-各アルゴリズムとデータ構造には独自のREADMEがあります
-関連する説明と、さらに読むためのリンク (関連YouTubeのビデオも含まれてい).
+
+各アルゴリズムとデータ構造には独自のREADMEがあります。
+関連する説明と、さらに読むためのリンク (関連YouTubeのビデオ)も含まれています。

 _Read this in other languages:_
 [_English_](https://github.com/trekhleb/javascript-algorithms/),
@ -36,10 +36,10 @@ _Read this in other languages:_
 * `B` [ヒープ](src/data-structures/heap) - max and min heap versions
 * `B` [優先度キュー](src/data-structures/priority-queue)
 * `A` [トライ](src/data-structures/trie)
-* `A` [リー](src/data-structures/tree)
+* `A` [ツリー](src/data-structures/tree)
  * `A` [バイナリ検索ツリー](src/data-structures/tree/binary-search-tree)
  * `A` [AVLツリー](src/data-structures/tree/avl-tree)
-  * `A` [赤黒のリー](src/data-structures/tree/red-black-tree)
+  * `A` [赤黒のツリー](src/data-structures/tree/red-black-tree)
  * `A` [セグメントツリー](src/data-structures/tree/segment-tree) - with min/max/sum range queries examples
  * `A` [フェンウィック・ツリー](src/data-structures/tree/fenwick-tree) (Binary Indexed Tree)
 * `A` [グラフ](src/data-structures/graph) (both directed and undirected)
--- a/README.md
+++ b/README.md
@ -73,6 +73,7 @@ a set of rules that precisely define a sequence of operations.
  * `B` [Radian & Degree](src/algorithms/math/radian) - radians to degree and backwards conversion
  * `B` [Fast Powering](src/algorithms/math/fast-powering)
  * `A` [Integer Partition](src/algorithms/math/integer-partition)
+  * `A` [Square Root](src/algorithms/math/square-root) - Newton's method
  * `A` [Liu Hui π Algorithm](src/algorithms/math/liu-hui) - approximate π calculations based on N-gons
  * `A` [Discrete Fourier Transform](src/algorithms/math/fourier-transform) - decompose a function of time (a signal) into the frequencies that make it up 
 * **Sets**
@ -279,7 +280,7 @@ Below is the list of some of the most used Big O notations and their performance
 | **Array**               | 1         | n         | n         | n         |           |
 | **Stack**               | n         | n         | 1         | 1         |           |
 | **Queue**               | n         | n         | 1         | 1         |           |
-| **Linked List**         | n         | n         | 1         | 1         |           |
+| **Linked List**         | n         | n         | 1         | n         |           |
 | **Hash Table**          | -         | n         | n         | n         | In case of perfect hash function costs would be O(1) |
 | **Binary Search Tree**  | n         | n         | n         | n         | In case of balanced tree costs would be O(log(n)) |
 | **B-Tree**              | log(n)    | log(n)    | log(n)    | log(n)    |           |
--- a/README.pt-BR.md
+++ b/README.pt-BR.md
@ -29,23 +29,23 @@ os dados.

 `B` - Iniciante, `A` - Avançado

-* `B` [Linked List](src/data-structures/linked-list)
-* `B` [Doubly Linked List](src/data-structures/doubly-linked-list)
-* `B` [Queue](src/data-structures/queue)
-* `B` [Stack](src/data-structures/stack)
-* `B` [Hash Table](src/data-structures/hash-table)
-* `B` [Heap](src/data-structures/heap)
-* `B` [Priority Queue](src/data-structures/priority-queue)
-* `A` [Trie](src/data-structures/trie)
-* `A` [Tree](src/data-structures/tree)
-  * `A` [Binary Search Tree](src/data-structures/tree/binary-search-tree)
-  * `A` [AVL Tree](src/data-structures/tree/avl-tree)
-  * `A` [Red-Black Tree](src/data-structures/tree/red-black-tree)
-  * `A` [Segment Tree](src/data-structures/tree/segment-tree) - com exemplos de consultas min / max / sum range
-  * `A` [Fenwick Tree](src/data-structures/tree/fenwick-tree) (Árvore indexada binária)
-* `A` [Graph](src/data-structures/graph) (ambos dirigidos e não direcionados)
-* `A` [Disjoint Set](src/data-structures/disjoint-set)
-* `A` [Bloom Filter](src/data-structures/bloom-filter)
+* `B` [Lista Encadeada (Linked List)](src/data-structures/linked-list/README.pt-BR.md)
+* `B` [Lista Duplamente Ligada (Doubly Linked List)](src/data-structures/doubly-linked-list/README.pt-BR.md)
+* `B` [Fila (Queue)](src/data-structures/queue/README.pt-BR.md)
+* `B` [Stack](src/data-structures/stack/README.pt-BR.md)
+* `B` [Tabela de Hash (Hash Table)](src/data-structures/hash-table/README.pt-BR.md)
+* `B` [Heap](src/data-structures/heap/README.pt-BR.md)
+* `B` [Fila de Prioridade (Priority Queue)](src/data-structures/priority-queue/README.pt-BR.md)
+* `A` [Trie](src/data-structures/trie/README.pt-BR.md)
+* `A` [Árvore (Tree)](src/data-structures/tree/README.pt-BR.md)
+  * `A` [Árvore de Pesquisa Binária (Binary Search Tree)](src/data-structures/tree/binary-search-tree/README.pt-BR.md)
+  * `A` [Árvore AVL (AVL Tree)](src/data-structures/tree/avl-tree/README.pt-BR.md)
+  * `A` [Árvore Vermelha-Preta (Red-Black Tree)](src/data-structures/tree/red-black-tree/README.pt-BR.md)
+  * `A` [Árvore de Segmento (Segment Tree)](src/data-structures/tree/segment-tree/README.pt-BR.md) - com exemplos de consultas min / max / sum range
+  * `A` [Árvore Fenwick (Fenwick Tree)](src/data-structures/tree/fenwick-tree/README.pt-BR.md) (Árvore indexada binária)
+* `A` [Gráfico (Graph)](src/data-structures/graph/README.pt-BR.md) (ambos dirigidos e não direcionados)
+* `A` [Conjunto Disjuntor (Disjoint Set)](src/data-structures/disjoint-set/README.pt-BR.md)
+* `A` [Filtro Bloom (Bloom Filter)](src/data-structures/bloom-filter/README.pt-BR.md)

 ## Algoritmos

--- a/package-lock.json
+++ b/package-lock.json
--- a/package.json
+++ b/package.json
@ -8,10 +8,6 @@
    "test": "jest",
    "ci": "npm run lint && npm run test -- --coverage"
  },
-  "pre-commit": [
-    "lint",
-    "test"
-  ],
  "repository": {
    "type": "git",
    "url": "git+https://github.com/trekhleb/javascript-algorithms.git"
@ -37,17 +33,17 @@
  },
  "homepage": "https://github.com/trekhleb/javascript-algorithms#readme",
  "devDependencies": {
-    "@types/jest": "^23.3.10",
-    "babel-cli": "^6.26.0",
-    "babel-preset-env": "^1.7.0",
-    "eslint": "^5.9.0",
+    "@babel/cli": "^7.2.3",
+    "@babel/preset-env": "^7.3.4",
+    "@types/jest": "^24.0.9",
+    "eslint": "^5.15.1",
    "eslint-config-airbnb": "^17.1.0",
-    "eslint-plugin-import": "^2.14.0",
-    "eslint-plugin-jest": "^22.1.0",
-    "eslint-plugin-jsx-a11y": "^6.1.2",
-    "eslint-plugin-react": "^7.11.1",
-    "jest": "^23.6.0",
-    "pre-commit": "^1.2.2"
+    "eslint-plugin-import": "^2.16.0",
+    "eslint-plugin-jest": "^22.3.0",
+    "eslint-plugin-jsx-a11y": "^6.2.1",
+    "eslint-plugin-react": "^7.12.4",
+    "husky": "^1.3.1",
+    "jest": "^24.3.1"
  },
  "dependencies": {}
 }
--- a/src/algorithms/graph/breadth-first-search/README.md
+++ b/src/algorithms/graph/breadth-first-search/README.md
@ -13,3 +13,4 @@ nodes first, before moving to the next level neighbors.
 - [Wikipedia](https://en.wikipedia.org/wiki/Breadth-first_search)
 - [Tree Traversals (Inorder, Preorder and Postorder)](https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/)
 - [BFS vs DFS](https://www.geeksforgeeks.org/bfs-vs-dfs-binary-tree/)
+- [BFS Visualization](https://www.cs.usfca.edu/~galles/visualization/BFS.html)
--- a/src/algorithms/graph/depth-first-search/README.md
+++ b/src/algorithms/graph/depth-first-search/README.md
@ -13,3 +13,4 @@ along each branch before backtracking.
 - [Wikipedia](https://en.wikipedia.org/wiki/Depth-first_search)
 - [Tree Traversals (Inorder, Preorder and Postorder)](https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/)
 - [BFS vs DFS](https://www.geeksforgeeks.org/bfs-vs-dfs-binary-tree/)
+- [DFS Visualization](https://www.cs.usfca.edu/~galles/visualization/DFS.html)
--- a/src/algorithms/graph/dijkstra/dijkstra.js
+++ b/src/algorithms/graph/dijkstra/dijkstra.js
@ -1,30 +1,44 @@
 import PriorityQueue from '../../../data-structures/priority-queue/PriorityQueue';

 /**
- * @param {Graph} graph
- * @param {GraphVertex} startVertex
+ * @typedef {Object} ShortestPaths
+ * @property {Object} distances - shortest distances to all vertices
+ * @property {Object} previousVertices - shortest paths to all vertices.
+ */
+
+/**
+ * Implementation of Dijkstra algorithm of finding the shortest paths to graph nodes.
+ * @param {Graph} graph - graph we're going to traverse.
+ * @param {GraphVertex} startVertex - traversal start vertex.
+ * @return {ShortestPaths}
 */
 export default function dijkstra(graph, startVertex) {
+  // Init helper variables that we will need for Dijkstra algorithm.
  const distances = {};
  const visitedVertices = {};
  const previousVertices = {};
  const queue = new PriorityQueue();

  // Init all distances with infinity assuming that currently we can't reach
-  // any of the vertices except start one.
+  // any of the vertices except the start one.
  graph.getAllVertices().forEach((vertex) => {
    distances[vertex.getKey()] = Infinity;
    previousVertices[vertex.getKey()] = null;
  });
+
+  // We are already at the startVertex so the distance to it is zero.
  distances[startVertex.getKey()] = 0;

  // Init vertices queue.
  queue.add(startVertex, distances[startVertex.getKey()]);

+  // Iterate over the priority queue of vertices until it is empty.
  while (!queue.isEmpty()) {
+    // Fetch next closest vertex.
    const currentVertex = queue.poll();

-    graph.getNeighbors(currentVertex).forEach((neighbor) => {
+    // Iterate over every unvisited neighbor of the current vertex.
+    currentVertex.getNeighbors().forEach((neighbor) => {
      // Don't visit already visited vertices.
      if (!visitedVertices[neighbor.getKey()]) {
        // Update distances to every neighbor from current vertex.
@ -33,15 +47,16 @@ export default function dijkstra(graph, startVertex) {
        const existingDistanceToNeighbor = distances[neighbor.getKey()];
        const distanceToNeighborFromCurrent = distances[currentVertex.getKey()] + edge.weight;

+        // If we've found shorter path to the neighbor - update it.
        if (distanceToNeighborFromCurrent < existingDistanceToNeighbor) {
          distances[neighbor.getKey()] = distanceToNeighborFromCurrent;

-          // Change priority.
+          // Change priority of the neighbor in a queue since it might have became closer.
          if (queue.hasValue(neighbor)) {
            queue.changePriority(neighbor, distances[neighbor.getKey()]);
          }

-          // Remember previous vertex.
+          // Remember previous closest vertex.
          previousVertices[neighbor.getKey()] = currentVertex;
        }

@ -52,10 +67,12 @@ export default function dijkstra(graph, startVertex) {
      }
    });

-    // Add current vertex to visited ones.
+    // Add current vertex to visited ones to avoid visiting it again later.
    visitedVertices[currentVertex.getKey()] = currentVertex;
  }

+  // Return the set of shortest distances to all vertices and the set of
+  // shortest paths to all vertices in a graph.
  return {
    distances,
    previousVertices,
--- a/src/algorithms/math/bits/README.md
+++ b/src/algorithms/math/bits/README.md
@ -137,7 +137,7 @@ a * b can be written in the below formats:
 ```

 The advantage of this approach is that in each recursive step one of the operands
-reduces to half its original value. Hence, the run time complexity is `O(log(b)` where `b` is
+reduces to half its original value. Hence, the run time complexity is `O(log(b))` where `b` is
 the operand that reduces to half on each recursive step.

 > See [multiply.js](multiply.js) for further details.
@ -226,6 +226,42 @@ Number: 9 = (10 - 1) = 0b01001

 > See [isPowerOfTwo.js](isPowerOfTwo.js) for further details.

+#### Full Adder
+
+This method adds up two integer numbers using bitwise operators.
+
+It implements [full adder](https://en.wikipedia.org/wiki/Adder_(electronics))
+electronics circuit logic to sum two 32-bit integers in two's complement format.
+It's using the boolean logic to cover all possible cases of adding two input bits:
+with and without a "carry bit" from adding the previous less-significant stage.
+
+Legend:
+- `A`: Number `A`
+- `B`: Number `B`
+- `ai`: ith bit of number `A`
+- `bi`: ith bit of number `B`
+- `carryIn`: a bit carried in from the previous less-significant stage
+- `carryOut`: a bit to carry to the next most-significant stage
+- `bitSum`: The sum of `ai`, `bi`, and `carryIn`
+- `resultBin`: The full result of adding current stage with all less-significant stages (in binary)
+- `resultDec`: The full result of adding current stage with all less-significant stages (in decimal)
+
+```
+A = 3: 011
+B = 6: 110
+┌──────┬────┬────┬─────────┬──────────┬─────────┬───────────┬───────────┐
+│  bit │ ai │ bi │ carryIn │ carryOut │  bitSum │ resultBin │ resultDec │
+├──────┼────┼────┼─────────┼──────────┼─────────┼───────────┼───────────┤
+│   0  │ 1  │ 0  │    0    │    0     │     1   │       1   │     1     │
+│   1  │ 1  │ 1  │    0    │    1     │     0   │      01   │     1     │
+│   2  │ 0  │ 1  │    1    │    1     │     0   │     001   │     1     │
+│   3  │ 0  │ 0  │    1    │    0     │     1   │    1001   │     9     │
+└──────┴────┴────┴─────────┴──────────┴─────────┴───────────┴───────────┘
+```
+
+> See [fullAdder.js](fullAdder.js) for further details.  
+> See [Full Adder on YouTube](https://www.youtube.com/watch?v=wvJc9CZcvBc&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8).
+
 ## References

 - [Bit Manipulation on YouTube](https://www.youtube.com/watch?v=NLKQEOgBAnw&t=0s&index=28&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
--- a/src/algorithms/math/bits/test/fullAdder.test.js
+++ b/src/algorithms/math/bits/test/fullAdder.test.js
@ -0,0 +1,18 @@
+import fullAdder from '../fullAdder';
+
+describe('fullAdder', () => {
+  it('should add up two numbers', () => {
+    expect(fullAdder(0, 0)).toBe(0);
+    expect(fullAdder(2, 0)).toBe(2);
+    expect(fullAdder(0, 2)).toBe(2);
+    expect(fullAdder(1, 2)).toBe(3);
+    expect(fullAdder(2, 1)).toBe(3);
+    expect(fullAdder(6, 6)).toBe(12);
+    expect(fullAdder(-2, 4)).toBe(2);
+    expect(fullAdder(4, -2)).toBe(2);
+    expect(fullAdder(-4, -4)).toBe(-8);
+    expect(fullAdder(4, -5)).toBe(-1);
+    expect(fullAdder(2, 121)).toBe(123);
+    expect(fullAdder(121, 2)).toBe(123);
+  });
+});
--- a/src/algorithms/math/bits/fullAdder.js
+++ b/src/algorithms/math/bits/fullAdder.js
@ -0,0 +1,70 @@
+import getBit from './getBit';
+
+/**
+ * Add two numbers using only binary operators.
+ *
+ * This is an implementation of full adders logic circuit.
+ * https://en.wikipedia.org/wiki/Adder_(electronics)
+ * Inspired by: https://www.youtube.com/watch?v=wvJc9CZcvBc
+ *
+ * Table(1)
+ *  INPUT  | OUT
+ *  C Ai Bi | C Si | Row
+ * -------- | -----| ---
+ *  0  0  0 | 0  0 | 1
+ *  0  0  1 | 0  1 | 2
+ *  0  1  0 | 0  1 | 3
+ *  0  1  1 | 1  0 | 4
+ * -------- | ---- | --
+ *  1  0  0 | 0  1 | 5
+ *  1  0  1 | 1  0 | 6
+ *  1  1  0 | 1  0 | 7
+ *  1  1  1 | 1  1 | 8
+ * ---------------------
+ *
+ * Legend:
+ * INPUT C = Carry in, from the previous less-significant stage
+ * INPUT Ai = ith bit of Number A
+ * INPUT Bi = ith bit of Number B
+ * OUT C = Carry out to the next most-significant stage
+ * OUT Si = Bit Sum, ith least significant bit of the result
+ *
+ *
+ * @param {number} a
+ * @param {number} b
+ * @return {number}
+ */
+export default function fullAdder(a, b) {
+  let result = 0;
+  let carry = 0;
+
+  // The operands of all bitwise operators are converted to signed
+  // 32-bit integers in two's complement format.
+  // https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Operators/Bitwise_Operators#Signed_32-bit_integers
+  for (let i = 0; i < 32; i += 1) {
+    const ai = getBit(a, i);
+    const bi = getBit(b, i);
+    const carryIn = carry;
+
+    // Calculate binary Ai + Bi without carry (half adder)
+    // See Table(1) rows 1 - 4: Si = Ai ^ Bi
+    const aiPlusBi = ai ^ bi;
+
+    // Calculate ith bit of the result by adding the carry bit to Ai + Bi
+    // For Table(1) rows 5 - 8 carryIn = 1: Si = Ai ^ Bi ^ 1, flip the bit
+    // Fpr Table(1) rows 1 - 4 carryIn = 0: Si = Ai ^ Bi ^ 0, a no-op.
+    const bitSum = aiPlusBi ^ carryIn;
+
+    // Carry out one to the next most-significant stage
+    // when at least one of these is true:
+    // 1) Table(1) rows 6, 7: one of Ai OR Bi is 1 AND carryIn = 1
+    // 2) Table(1) rows 4, 8: Both Ai AND Bi are 1
+    const carryOut = (aiPlusBi & carryIn) | (ai & bi);
+    carry = carryOut;
+
+    // Set ith least significant bit of the result to bitSum.
+    result |= bitSum << i;
+  }
+
+  return result;
+}
--- a/src/algorithms/math/square-root/README.md
+++ b/src/algorithms/math/square-root/README.md
@ -0,0 +1,62 @@
+# Square Root (Newton's Method)
+
+In numerical analysis, a branch of mathematics, there are several square root 
+algorithms or methods of computing the principal square root of a non-negative real 
+number. As, generally, the roots of a function cannot be computed exactly.
+The root-finding algorithms provide approximations to roots expressed as floating
+point numbers.
+
+Finding ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/bff86975b0e7944720b3e635c53c22c032a7a6f1) is
+the same as solving the equation ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cf57722151ef19ba1ca918d702b95c335e21cad) for a
+positive `x`. Therefore, any general numerical root-finding algorithm can be used.
+
+**Newton's method** (also known as the Newton–Raphson method), named after 
+_Isaac Newton_ and _Joseph Raphson_, is one example of a root-finding algorithm. It is a 
+method for finding successively better approximations to the roots of a real-valued function.
+
+Let's start by explaining the general idea of Newton's method and then apply it to our particular
+case with finding a square root of the number.
+
+## Newton's Method General Idea
+
+The Newton–Raphson method in one variable is implemented as follows:
+
+The method starts with a function `f` defined over the real numbers `x`, the function's derivative `f'`, and an 
+initial guess `x0` for a root of the function `f`. If the function satisfies the assumptions made in the derivation 
+of the formula and the initial guess is close, then a better approximation `x1` is:
+
+![](https://wikimedia.org/api/rest_v1/media/math/render/svg/52c50eca0b7c4d64ef2fdca678665b73e944cb84)
+
+Geometrically, `(x1, 0)` is the intersection of the `x`-axis and the tangent of 
+the graph of `f` at `(x0, f (x0))`.
+
+The process is repeated as:
+
+![](https://wikimedia.org/api/rest_v1/media/math/render/svg/710c11b9ec4568d1cfff49b7c7d41e0a7829a736)
+
+until a sufficiently accurate value is reached.
+
+![](https://upload.wikimedia.org/wikipedia/commons/e/e0/NewtonIteration_Ani.gif)
+
+## Newton's Method of Finding a Square Root
+
+As it was mentioned above, finding ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/bff86975b0e7944720b3e635c53c22c032a7a6f1) is
+the same as solving the equation ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cf57722151ef19ba1ca918d702b95c335e21cad) for a
+positive `x`.
+
+The derivative of the function `f(x)` in case of square root problem is `2x`.
+
+After applying the Newton's formula (see above) we get the following equation for our algorithm iterations:
+
+```text
+x := x - (x² - S) / (2x)
+```
+
+The `x² − S` above is how far away `x²` is from where it needs to be, and the 
+division by `2x` is the derivative of `x²`, to scale how much we adjust `x` by how 
+quickly `x²` is changing.
+
+## References
+
+- [Methods of computing square roots on Wikipedia](https://en.wikipedia.org/wiki/Methods_of_computing_square_roots)
+- [Newton's method on Wikipedia](https://en.wikipedia.org/wiki/Newton%27s_method)
--- a/src/algorithms/math/square-root/test/squareRoot.test.js
+++ b/src/algorithms/math/square-root/test/squareRoot.test.js
@ -0,0 +1,69 @@
+import squareRoot from '../squareRoot';
+
+describe('squareRoot', () => {
+  it('should throw for negative numbers', () => {
+    function failingSquareRoot() {
+      squareRoot(-5);
+    }
+    expect(failingSquareRoot).toThrow();
+  });
+
+  it('should correctly calculate square root with default tolerance', () => {
+    expect(squareRoot(0)).toBe(0);
+    expect(squareRoot(1)).toBe(1);
+    expect(squareRoot(2)).toBe(1);
+    expect(squareRoot(3)).toBe(2);
+    expect(squareRoot(4)).toBe(2);
+    expect(squareRoot(15)).toBe(4);
+    expect(squareRoot(16)).toBe(4);
+    expect(squareRoot(256)).toBe(16);
+    expect(squareRoot(473)).toBe(22);
+    expect(squareRoot(14723)).toBe(121);
+  });
+
+  it('should correctly calculate square root for integers with custom tolerance', () => {
+    let tolerance = 1;
+
+    expect(squareRoot(0, tolerance)).toBe(0);
+    expect(squareRoot(1, tolerance)).toBe(1);
+    expect(squareRoot(2, tolerance)).toBe(1.4);
+    expect(squareRoot(3, tolerance)).toBe(1.8);
+    expect(squareRoot(4, tolerance)).toBe(2);
+    expect(squareRoot(15, tolerance)).toBe(3.9);
+    expect(squareRoot(16, tolerance)).toBe(4);
+    expect(squareRoot(256, tolerance)).toBe(16);
+    expect(squareRoot(473, tolerance)).toBe(21.7);
+    expect(squareRoot(14723, tolerance)).toBe(121.3);
+
+    tolerance = 3;
+
+    expect(squareRoot(0, tolerance)).toBe(0);
+    expect(squareRoot(1, tolerance)).toBe(1);
+    expect(squareRoot(2, tolerance)).toBe(1.414);
+    expect(squareRoot(3, tolerance)).toBe(1.732);
+    expect(squareRoot(4, tolerance)).toBe(2);
+    expect(squareRoot(15, tolerance)).toBe(3.873);
+    expect(squareRoot(16, tolerance)).toBe(4);
+    expect(squareRoot(256, tolerance)).toBe(16);
+    expect(squareRoot(473, tolerance)).toBe(21.749);
+    expect(squareRoot(14723, tolerance)).toBe(121.338);
+
+    tolerance = 10;
+
+    expect(squareRoot(0, tolerance)).toBe(0);
+    expect(squareRoot(1, tolerance)).toBe(1);
+    expect(squareRoot(2, tolerance)).toBe(1.4142135624);
+    expect(squareRoot(3, tolerance)).toBe(1.7320508076);
+    expect(squareRoot(4, tolerance)).toBe(2);
+    expect(squareRoot(15, tolerance)).toBe(3.8729833462);
+    expect(squareRoot(16, tolerance)).toBe(4);
+    expect(squareRoot(256, tolerance)).toBe(16);
+    expect(squareRoot(473, tolerance)).toBe(21.7485631709);
+    expect(squareRoot(14723, tolerance)).toBe(121.3383698588);
+  });
+
+  it('should correctly calculate square root for integers with custom tolerance', () => {
+    expect(squareRoot(4.5, 10)).toBe(2.1213203436);
+    expect(squareRoot(217.534, 10)).toBe(14.7490338667);
+  });
+});
--- a/src/algorithms/math/square-root/squareRoot.js
+++ b/src/algorithms/math/square-root/squareRoot.js
@ -0,0 +1,40 @@
+/**
+ * Calculates the square root of the number with given tolerance (precision)
+ * by using Newton's method.
+ *
+ * @param number - the number we want to find a square root for.
+ * @param [tolerance] - how many precise numbers after the floating point we want to get.
+ * @return {number}
+ */
+export default function squareRoot(number, tolerance = 0) {
+  // For now we won't support operations that involves manipulation with complex numbers.
+  if (number < 0) {
+    throw new Error('The method supports only positive integers');
+  }
+
+  // Handle edge case with finding the square root of zero.
+  if (number === 0) {
+    return 0;
+  }
+
+  // We will start approximation from value 1.
+  let root = 1;
+
+  // Delta is a desired distance between the number and the square of the root.
+  // - if tolerance=0 then delta=1
+  // - if tolerance=1 then delta=0.1
+  // - if tolerance=2 then delta=0.01
+  // - and so on...
+  const requiredDelta = 1 / (10 ** tolerance);
+
+  // Approximating the root value to the point when we get a desired precision.
+  while (Math.abs(number - (root ** 2)) > requiredDelta) {
+    // Newton's method reduces in this case to the so-called Babylonian method.
+    // These methods generally yield approximate results, but can be made arbitrarily
+    // precise by increasing the number of calculation steps.
+    root -= ((root ** 2) - number) / (2 * root);
+  }
+
+  // Cut off undesired floating digits and return the root value.
+  return Math.round(root * (10 ** tolerance)) / (10 ** tolerance);
+}
--- a/src/algorithms/sets/combinations/combineWithRepetitions.js
+++ b/src/algorithms/sets/combinations/combineWithRepetitions.js
@ -4,6 +4,8 @@
 * @return {*[]}
 */
 export default function combineWithRepetitions(comboOptions, comboLength) {
+  // If the length of the combination is 1 then each element of the original array
+  // is a combination itself.
  if (comboLength === 1) {
    return comboOptions.map(comboOption => [comboOption]);
  }
@ -11,14 +13,16 @@ export default function combineWithRepetitions(comboOptions, comboLength) {
  // Init combinations array.
  const combos = [];

-  // Eliminate characters one by one and concatenate them to
-  // combinations of smaller lengths.
+  // Remember characters one by one and concatenate them to combinations of smaller lengths.
+  // We don't extract elements here because the repetitions are allowed.
  comboOptions.forEach((currentOption, optionIndex) => {
+    // Generate combinations of smaller size.
    const smallerCombos = combineWithRepetitions(
      comboOptions.slice(optionIndex),
      comboLength - 1,
    );

+    // Concatenate currentOption with all combinations of smaller size.
    smallerCombos.forEach((smallerCombo) => {
      combos.push([currentOption].concat(smallerCombo));
    });
--- a/src/algorithms/sets/combinations/combineWithoutRepetitions.js
+++ b/src/algorithms/sets/combinations/combineWithoutRepetitions.js
@ -4,6 +4,8 @@
 * @return {*[]}
 */
 export default function combineWithoutRepetitions(comboOptions, comboLength) {
+  // If the length of the combination is 1 then each element of the original array
+  // is a combination itself.
  if (comboLength === 1) {
    return comboOptions.map(comboOption => [comboOption]);
  }
@ -11,14 +13,16 @@ export default function combineWithoutRepetitions(comboOptions, comboLength) {
  // Init combinations array.
  const combos = [];

-  // Eliminate characters one by one and concatenate them to
-  // combinations of smaller lengths.
+  // Extract characters one by one and concatenate them to combinations of smaller lengths.
+  // We need to extract them because we don't want to have repetitions after concatenation.
  comboOptions.forEach((currentOption, optionIndex) => {
+    // Generate combinations of smaller size.
    const smallerCombos = combineWithoutRepetitions(
      comboOptions.slice(optionIndex + 1),
      comboLength - 1,
    );

+    // Concatenate currentOption with all combinations of smaller size.
    smallerCombos.forEach((smallerCombo) => {
      combos.push([currentOption].concat(smallerCombo));
    });
--- a/src/algorithms/sorting/quick-sort/QuickSortInPlace.js
+++ b/src/algorithms/sorting/quick-sort/QuickSortInPlace.js
@ -46,7 +46,7 @@ export default class QuickSortInPlace extends Sort {

      const pivot = array[highIndex];
      // visitingCallback is used for time-complexity analysis.
-      this.callbacks.visitingCallback(array[pivot]);
+      this.callbacks.visitingCallback(pivot);

      let partitionIndex = lowIndex;
      for (let currentIndex = lowIndex; currentIndex < highIndex; currentIndex += 1) {
--- a/src/algorithms/sorting/radix-sort/README.md
+++ b/src/algorithms/sorting/radix-sort/README.md
@ -7,6 +7,13 @@ is required, but because integers can represent strings of characters
 (e.g., names or dates) and specially formatted floating point numbers, radix 
 sort is not limited to integers.

+*Where does the name come from?*
+
+In mathematical numeral systems, the *radix* or base is the number of unique digits,
+including the digit zero, used to represent numbers in a positional numeral system. 
+For example, a binary system (using numbers 0 and 1) has a radix of 2 and a decimal 
+system (using numbers 0 to 9) has a radix of 10.
+
 ## Efficiency

 The topic of the efficiency of radix sort compared to other sorting algorithms is 
--- a/src/algorithms/string/levenshtein-distance/README.md
+++ b/src/algorithms/string/levenshtein-distance/README.md
@ -106,7 +106,7 @@ bottom-up direction) is being applied here.
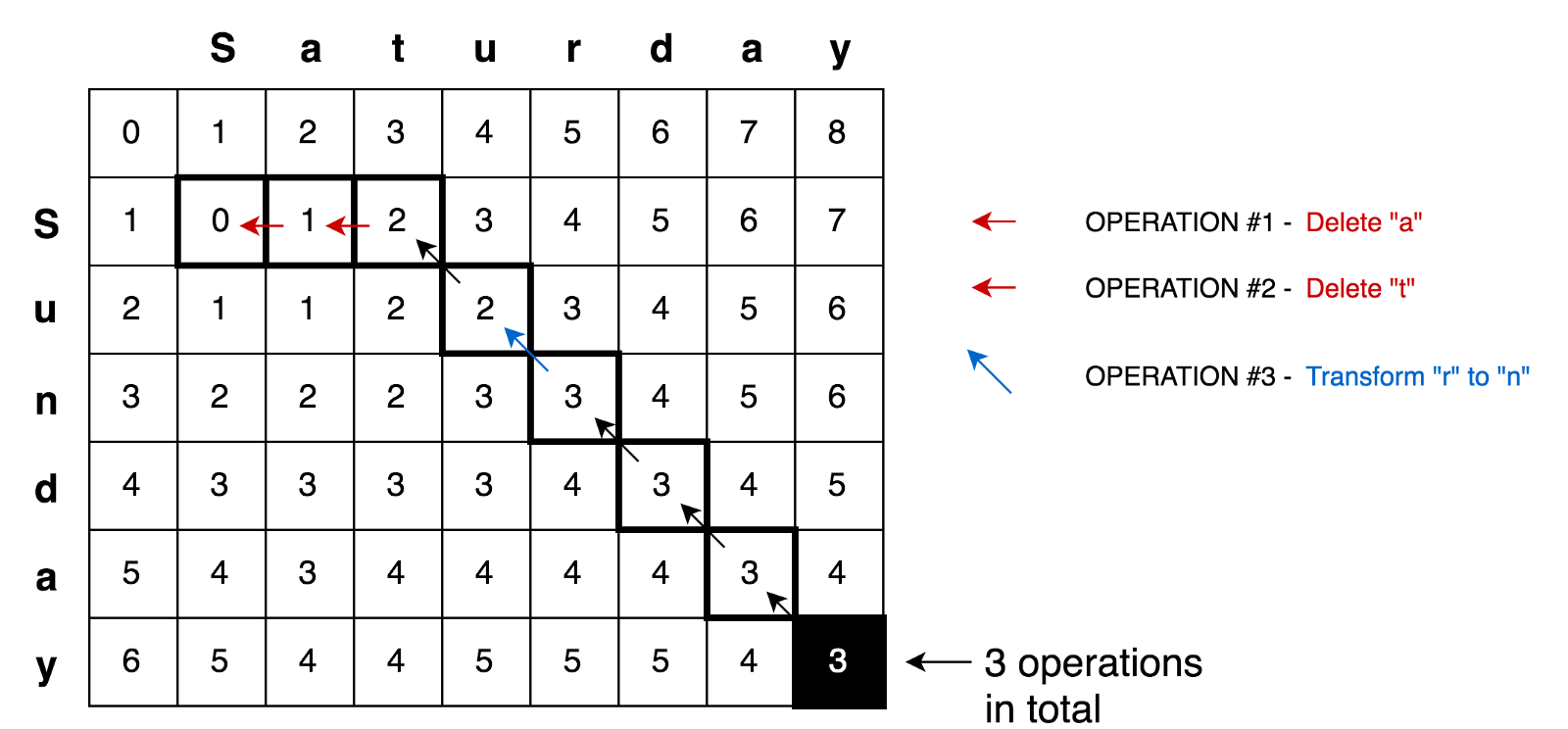
 Applying this principle further we may solve more complicated cases like 
 with `Saturday → Sunday` transformation.

-![Levenshtein distance](https://cdn-images-1.medium.com/max/1600/1*geMdmZcdU1bZbHIoh6KO3Q.png)
+![Levenshtein distance](https://cdn-images-1.medium.com/max/2600/1*497gMaFErzJpCXG7kS_7dw.png)

 ## References

--- a/src/algorithms/tree/depth-first-search/depthFirstSearch.js
+++ b/src/algorithms/tree/depth-first-search/depthFirstSearch.js
@ -1,52 +1,76 @@
 /**
- * @typedef {Object} Callbacks
- * @property {function(node: BinaryTreeNode, child: BinaryTreeNode): boolean} allowTraversal -
- *   Determines whether DFS should traverse from the node to its child.
+ * @typedef {Object} TraversalCallbacks
+ *
+ * @property {function(node: BinaryTreeNode, child: BinaryTreeNode): boolean} allowTraversal
+ * - Determines whether DFS should traverse from the node to its child.
+ *
 * @property {function(node: BinaryTreeNode)} enterNode - Called when DFS enters the node.
+ *
 * @property {function(node: BinaryTreeNode)} leaveNode - Called when DFS leaves the node.
 */

 /**
- * @param {Callbacks} [callbacks]
- * @returns {Callbacks}
+ * Extend missing traversal callbacks with default callbacks.
+ *
+ * @param {TraversalCallbacks} [callbacks] - The object that contains traversal callbacks.
+ * @returns {TraversalCallbacks} - Traversal callbacks extended with defaults callbacks.
 */
 function initCallbacks(callbacks = {}) {
-  const initiatedCallback = callbacks;
+  // Init empty callbacks object.
+  const initiatedCallbacks = {};

+  // Empty callback that we will use in case if user didn't provide real callback function.
  const stubCallback = () => {};
-  const defaultAllowTraversal = () => true;
+  // By default we will allow traversal of every node
+  // in case if user didn't provide a callback for that.
+  const defaultAllowTraversalCallback = () => true;

-  initiatedCallback.allowTraversal = callbacks.allowTraversal || defaultAllowTraversal;
-  initiatedCallback.enterNode = callbacks.enterNode || stubCallback;
-  initiatedCallback.leaveNode = callbacks.leaveNode || stubCallback;
+  // Copy original callbacks to our initiatedCallbacks object or use default callbacks instead.
+  initiatedCallbacks.allowTraversal = callbacks.allowTraversal || defaultAllowTraversalCallback;
+  initiatedCallbacks.enterNode = callbacks.enterNode || stubCallback;
+  initiatedCallbacks.leaveNode = callbacks.leaveNode || stubCallback;

-  return initiatedCallback;
+  // Returned processed list of callbacks.
+  return initiatedCallbacks;
 }

 /**
- * @param {BinaryTreeNode} node
- * @param {Callbacks} callbacks
+ * Recursive depth-first-search traversal for binary.
+ *
+ * @param {BinaryTreeNode} node - binary tree node that we will start traversal from.
+ * @param {TraversalCallbacks} callbacks - the object that contains traversal callbacks.
 */
 export function depthFirstSearchRecursive(node, callbacks) {
+  // Call the "enterNode" callback to notify that the node is going to be entered.
  callbacks.enterNode(node);

-  // Traverse left branch.
+  // Traverse left branch only if case if traversal of the left node is allowed.
  if (node.left && callbacks.allowTraversal(node, node.left)) {
    depthFirstSearchRecursive(node.left, callbacks);
  }

-  // Traverse right branch.
+  // Traverse right branch only if case if traversal of the right node is allowed.
  if (node.right && callbacks.allowTraversal(node, node.right)) {
    depthFirstSearchRecursive(node.right, callbacks);
  }

+  // Call the "leaveNode" callback to notify that traversal
+  // of the current node and its children is finished.
  callbacks.leaveNode(node);
 }

 /**
- * @param {BinaryTreeNode} rootNode
- * @param {Callbacks} [callbacks]
+ * Perform depth-first-search traversal of the rootNode.
+ * For every traversal step call "allowTraversal", "enterNode" and "leaveNode" callbacks.
+ * See TraversalCallbacks type definition for more details about the shape of callbacks object.
+ *
+ * @param {BinaryTreeNode} rootNode - The node from which we start traversing.
+ * @param {TraversalCallbacks} [callbacks] - Traversal callbacks.
 */
 export default function depthFirstSearch(rootNode, callbacks) {
-  depthFirstSearchRecursive(rootNode, initCallbacks(callbacks));
+  // In case if user didn't provide some callback we need to replace them with default ones.
+  const processedCallbacks = initCallbacks(callbacks);
+
+  // Now, when we have all necessary callbacks we may proceed to recursive traversal.
+  depthFirstSearchRecursive(rootNode, processedCallbacks);
 }
--- a/src/data-structures/bloom-filter/README.md
+++ b/src/data-structures/bloom-filter/README.md
@ -1,5 +1,9 @@
 # Bloom Filter

+_Read this in other languages:_
+[_Русский_](README.ru-RU.md),
+[_Português_](README.pt-BR.md)
+
 A **bloom filter** is a space-efficient probabilistic 
 data structure designed to test whether an element 
 is present in a set. It is designed to be blazingly 
--- a/src/data-structures/bloom-filter/README.pt-BR.md
+++ b/src/data-structures/bloom-filter/README.pt-BR.md
@ -0,0 +1,129 @@
+# Filtro Bloom (Bloom Filter)
+
+O **bloom filter** é uma estrutura de dados probabilística
+espaço-eficiente designada para testar se um elemento está
+ou não presente em um conjunto de dados. Foi projetado para ser
+incrivelmente rápido e utilizar o mínimo de memória ao 
+potencial custo de um falso-positivo. Correspondências 
+_falsas positivas_ são possíveis, contudo _falsos negativos_ 
+não são - em outras palavras, a consulta retorna 
+"possivelmente no conjunto" ou "definitivamente não no conjunto".
+
+Bloom propôs a técnica para aplicações onde a quantidade 
+de entrada de dados exigiria uma alocação de memória
+impraticavelmente grande se as "convencionais" técnicas
+error-free hashing fossem aplicado.
+
+## Descrição do algoritmo
+
+Um filtro Bloom vazio é um _bit array_ de `m` bits, todos
+definidos como `0`. Também deverá haver diferentes funções
+de hash `k` definidas, cada um dos quais mapeia e produz hash
+para um dos elementos definidos em uma das posições `m` da
+ _array_, gerando uma distribuição aleatória e uniforme.
+Normalmente, `k` é uma constante, muito menor do que `m`,
+pelo qual é proporcional ao número de elements a ser adicionado;
+a escolha precisa de `k` e a constante de proporcionalidade de `m`
+são determinadas pela taxa de falsos positivos planejado do filtro.
+
+Aqui está um exemplo de um filtro Bloom, representando o
+conjunto `{x, y, z}`. As flechas coloridas demonstram as
+posições no _bit array_ em que cada elemento é mapeado.
+O elemento `w` não está definido dentro de `{x, y, z}`,
+porque este produz hash para uma posição de array de bits
+contendo `0`. Para esta imagem: `m = 18` e `k = 3`.
+
+![Bloom Filter](https://upload.wikimedia.org/wikipedia/commons/a/ac/Bloom_filter.svg)
+
+## Operações
+
+Existem duas operações principais que o filtro Bloom pode operar:
+_inserção_ e _pesquisa_. A pesquisa pode resultar em falsos
+positivos. Remoção não é possível.
+
+Em outras palavras, o filtro pode receber itens. Quando
+vamos verificar se um item já foi anteriormente
+inserido, ele poderá nos dizer "não" ou "talvez".
+
+Ambas as inserções e pesquisas são operações `O(1)`.
+
+## Criando o filtro
+
+Um filtro Bloom é criado ao alocar um certo tamanho.
+No nosso exemplo, nós utilizamos `100` como tamanho padrão.
+Todas as posições são initializadas como `false`.
+
+### Inserção
+
+Durante a inserção, um número de função hash, no nosso caso `3`
+funções de hash, são utilizadas para criar hashes de uma entrada.
+Estas funções de hash emitem saída de índices. A cada índice
+recebido, nós simplismente trocamos o valor de nosso filtro
+Bloom para `true`.
+
+### Pesquisa
+
+Durante a pesquisa, a mesma função de hash é chamada
+e usada para emitir hash da entrada. Depois nós checamos
+se _todos_ os indices recebidos possuem o valor `true`
+dentro de nosso filtro Bloom. Caso _todos_ possuam o valor
+`true`, nós sabemos que o filtro Bloom pode ter tido
+o valor inserido anteriormente.
+
+Contudo, isto não é certeza, porque é possível que outros
+valores anteriormente inseridos trocaram o valor para `true`.
+Os valores não são necessariamente `true` devido ao ítem
+atualmente sendo pesquisado. A certeza absoluta é impossível,
+a não ser que apenas um item foi inserido anteriormente.
+
+Durante a checagem do filtro Bloom para índices retornados
+pela nossa função de hash, mesmo que apenas um deles possua
+valor como `false`, nós definitivamente sabemos que o ítem
+não foi anteriormente inserido.
+
+## Falso Positivos
+
+A probabilidade de falso positivos é determinado por
+três fatores: o tamanho do filtro de Bloom, o número de 
+funções de hash que utilizados, e o número de itens que
+foram inseridos dentro do filtro.
+
+A formula para calcular a probabilidade de um falso positivo é:
+
+( 1 - e <sup>-kn/m</sup> ) <sup>k</sup>
+
+`k` = número de funções de hash
+
+`m` = tamanho do filtro
+
+`n` = número de itens inserido
+
+Estas variáveis, `k`, `m` e `n`, devem ser escolhidas baseado
+em quanto aceitável são os falsos positivos. Se os valores
+escolhidos resultam em uma probabilidade muito alta, então
+os valores devem ser ajustados e a probabilidade recalculada.
+
+## Aplicações
+
+Um filtro Bloom pode ser utilizado em uma página de Blog.
+Se o objetivo é mostrar aos leitores somente os artigos
+em que eles nunca viram, então o filtro Bloom é perfeito 
+para isso. Ele pode armazenar hashes baseados nos artigos.
+Depois que um usuário lê alguns artigos, eles podem ser
+inseridos dentro do filtro. Na próxima vez que o usuário
+visitar o Blog, aqueles artigos poderão ser filtrados (eliminados) 
+do resultado.
+
+Alguns artigos serão inevitavelmente filtrados (eliminados) 
+por engano, mas o custo é aceitável. Tudo bem se um usuário nunca
+ver alguns poucos artigos, desde que tenham outros novos
+para ver toda vez que eles visitam o site. 
+
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Bloom_filter)
+- [Bloom Filters by Example](http://llimllib.github.io/bloomfilter-tutorial/)
+- [Calculating False Positive Probability](https://hur.st/bloomfilter/?n=4&p=&m=18&k=3)
+- [Bloom Filters on Medium](https://blog.medium.com/what-are-bloom-filters-1ec2a50c68ff)
+- [Bloom Filters on YouTube](https://www.youtube.com/watch?v=bEmBh1HtYrw)
--- a/src/data-structures/bloom-filter/README.ru-RU.md
+++ b/src/data-structures/bloom-filter/README.ru-RU.md
@ -0,0 +1,55 @@
+# Фильтр Блума
+
+**Фильтр Блума** - это пространственно-эффективная вероятностная структура данных, созданная для проверки наличия элемента
+в множестве. Он спроектирован невероятно быстрым при минимальном использовании памяти ценой потенциальных ложных срабатываний.
+Существует возможность получить ложноположительное срабатывание (элемента в множестве нет, но структура данных сообщает,
+что он есть), но не ложноотрицательное. Другими словами, очередь возвращает или "возможно в наборе", или "определённо не
+в наборе". Фильтр Блума может использовать любой объём памяти, однако чем он больше, тем меньше вероятность ложного
+срабатывания. 
+
+Блум предложил эту технику для применения в областях, где количество исходных данных потребовало бы непрактично много 
+памяти, в случае применения условно безошибочных техник хеширования.
+
+## Описание алгоритма
+
+Пустой фильтр Блума представлен битовым массивом из `m` битов, все биты которого обнулены. Должно быть определено `k`
+независимых хеш-функций, отображающих каждый элемент множества в одну из `m` позиций в массиве, генерируя единообразное
+случайное распределение. Обычно `k` задана константой, которая много меньше `m` и пропорциональна
+количеству добавляемых элементов; точный выбор `k` и постоянной пропорциональности `m` определяются уровнем ложных
+срабатываний фильтра.
+
+Вот пример Блум фильтра, представляющего набор `{x, y, z}`. Цветные стрелки показывают позиции в битовом массиве,
+которым привязан каждый элемент набора. Элемент `w` не в набора `{x, y, z}`, потому что он привязан к позиции в битовом
+массиве, равной `0`. Для этой формы , `m = 18`, а `k = 3`.
+
+Фильтр Блума представляет собой битовый массив из `m` бит. Изначально, когда структура данных хранит пустое множество, все
+`m` бит обнулены. Пользователь должен определить `k` независимых хеш-функций `h1`, …, `hk`,
+отображающих каждый элемент в одну из `m` позиций битового массива достаточно равномерным образом.
+
+Для добавления элемента e необходимо записать единицы на каждую из позиций `h1(e)`, …, `hk(e)`
+битового массива.
+
+Для проверки принадлежности элемента `e` к множеству хранимых элементов, необходимо проверить состояние битов
+`h1(e)`, …, `hk(e)`. Если хотя бы один из них равен нулю, элемент не может принадлежать множеству
+(иначе бы при его добавлении все эти биты были установлены). Если все они равны единице, то структура данных сообщает,
+что `е` принадлежит множеству. При этом может возникнуть две ситуации: либо элемент действительно принадлежит множеству,
+либо все эти биты оказались установлены по случайности при добавлении других элементов, что и является источником ложных
+срабатываний в этой структуре данных.
+
+![Фильтр Блума](https://upload.wikimedia.org/wikipedia/commons/a/ac/Bloom_filter.svg)
+
+## Применения
+
+Фильтр Блума может быть использован для блогов. Если цель состоит в том, чтобы показать читателям только те статьи,
+которые они ещё не видели, фильтр блума идеален. Он может содержать хешированные значения, соответствующие статье. После
+того, как пользователь прочитал несколько статей, они могут быть помещены в фильтр. В следующий раз, когда пользователь
+посетит сайт, эти статьи могут быть убраны из результатов с помощью фильтра.
+
+Некоторые статьи неизбежно будут отфильтрованы по ошибке, но цена приемлема. То, что пользователь не увидит несколько
+статей в полне приемлемо, принимая во внимание тот факт, что ему всегда показываются другие новые статьи при каждом
+новом посещении.
+
+## Ссылки
+
+- [Wikipedia](https://ru.wikipedia.org/wiki/%D0%A4%D0%B8%D0%BB%D1%8C%D1%82%D1%80_%D0%91%D0%BB%D1%83%D0%BC%D0%B0)
+- [Фильтр Блума на Хабре](https://habr.com/ru/post/112069/)
--- a/src/data-structures/disjoint-set/README.md
+++ b/src/data-structures/disjoint-set/README.md
@ -1,5 +1,10 @@
 # Disjoint Set

+_Read this in other languages:_
+[_Русский_](README.ru-RU.md),
+[_Português_](README.pt-BR.md)
+
+
 **Disjoint-set** data structure (also called a union–find data structure or merge–find set) is a data 
 structure that tracks a set of elements partitioned into a number of disjoint (non-overlapping) subsets. 
 It provides near-constant-time operations (bounded by the inverse Ackermann function) to *add new sets*, 
--- a/src/data-structures/disjoint-set/README.pt-BR.md
+++ b/src/data-structures/disjoint-set/README.pt-BR.md
@ -0,0 +1,28 @@
+# Conjunto Disjuntor (Disjoint Set)
+
+**Conjunto Disjuntor**
+
+**Conjunto Disjuntor** é uma estrutura de dados (também chamado de
+estrutura de dados de union–find ou merge–find) é uma estrutura de dados
+que rastreia um conjunto de elementos particionados em um número de
+subconjuntos separados (sem sobreposição).
+Ele fornece operações de tempo quase constante (limitadas pela função
+inversa de Ackermann) para *adicionar novos conjuntos*, para 
+*mesclar/fundir conjuntos existentes* e para *determinar se os elementos
+estão no mesmo conjunto*.
+Além de muitos outros usos (veja a seção Applications), conjunto disjuntor
+desempenham um papel fundamental no algoritmo de Kruskal para encontrar a
+árvore geradora mínima de um gráfico (graph).
+
+![disjoint set](https://upload.wikimedia.org/wikipedia/commons/6/67/Dsu_disjoint_sets_init.svg)
+
+*MakeSet* cria 8 singletons.
+
+![disjoint set](https://upload.wikimedia.org/wikipedia/commons/a/ac/Dsu_disjoint_sets_final.svg)
+
+Depois de algumas operações de *Uniões*, alguns conjuntos são agrupados juntos.
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Disjoint-set_data_structure)
+- [By Abdul Bari on YouTube](https://www.youtube.com/watch?v=wU6udHRIkcc&index=14&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
--- a/src/data-structures/disjoint-set/README.ru-RU.md
+++ b/src/data-structures/disjoint-set/README.ru-RU.md
@ -0,0 +1,21 @@
+# Система непересекающихся множеств
+
+**Система непересекающихся множеств** это структура данных (также называемая структурой данной поиска пересечения или
+множеством поиска слияния), которая управляет множеством элементов, разбитых на несколько непересекающихся подмножеств.
+Она предоставляет около-константное время выполнения операций (ограниченное обратной функцией Акерманна) по *добавлению
+новых множеств*, *слиянию существующих множеств* и *опеределению, относятся ли элементы к одному и тому же множеству*.
+
+Применяется для хранения компонент связности в графах, в частности, алгоритму Краскала необходима подобная структура
+данных для эффективной реализации.
+
+Основные операции:
+
+- *MakeSet(x)* - создаёт одноэлементное множество {x},
+- *Find(x)* - возвращает идентификатор множества, содержащего элемент x,
+- *Union(x,y)* - объединение множеств, содержащих x и y.
+
+После некоторых операций *объединения*, некоторые множества собраны вместе
+
+## Ссылки
+- [СНМ на Wikipedia](https://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D0%BD%D0%B5%D0%BF%D0%B5%D1%80%D0%B5%D1%81%D0%B5%D0%BA%D0%B0%D1%8E%D1%89%D0%B8%D1%85%D1%81%D1%8F_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2)
+- [СНМ на YouTube](https://www.youtube.com/watch?v=bXBHYqNeBLo)
--- a/src/data-structures/doubly-linked-list/README.ja-JP.md
+++ b/src/data-structures/doubly-linked-list/README.ja-JP.md
@ -0,0 +1,95 @@
+# 双方向リスト
+
+コンピュータサイエンスにおいて、**双方向リスト**はノードと呼ばれる一連のリンクレコードからなる連結データ構造です。各ノードはリンクと呼ばれる2つのフィールドを持っていて、これらは一連のノード内における前のノードと次のノードを参照しています。最初のノードの前のリンクと最後のノードの次のリンクはある種の終端を示していて、一般的にはダミーノードやnullが格納され、リストのトラバースを容易に行えるようにしています。もしダミーノードが1つしかない場合、リストはその1つのノードを介して循環的にリンクされます。これは、それぞれ逆の順番の単方向のリンクリストが2つあるものとして考えることができます。
+
+![Doubly Linked List](https://upload.wikimedia.org/wikipedia/commons/5/5e/Doubly-linked-list.svg)
+
+2つのリンクにより、リストをどちらの方向にもトラバースすることができます。双方向リストはノードの追加や削除の際に、片方向リンクリストと比べてより多くのリンクを変更する必要があります。しかし、その操作は簡単で、より効率的な(最初のノード以外の場合)可能性があります。前のノードのリンクを更新する際に前のノードを保持したり、前のノードを見つけるためにリストをトラバースする必要がありません。
+
+## 基本操作の擬似コード
+
+### 挿入
+
+```text
+Add(value)
+  Pre: value is the value to add to the list
+  Post: value has been placed at the tail of the list
+  n ← node(value)
+  if head = ø
+    head ← n
+    tail ← n
+  else
+    n.previous ← tail
+    tail.next ← n
+    tail ← n
+  end if
+end Add
+```
+    
+### 削除
+
+```text
+Remove(head, value)
+  Pre: head is the head node in the list
+       value is the value to remove from the list
+  Post: value is removed from the list, true; otherwise false
+  if head = ø
+    return false
+  end if
+  if value = head.value
+    if head = tail
+      head ← ø
+      tail ← ø
+    else
+      head ← head.next
+      head.previous ← ø
+    end if
+    return true
+  end if
+  n ← head.next
+  while n = ø and value !== n.value
+    n ← n.next
+  end while
+  if n = tail
+    tail ← tail.previous
+    tail.next ← ø
+    return true
+  else if n = ø
+    n.previous.next ← n.next
+    n.next.previous ← n.previous
+    return true
+  end if
+  return false
+end Remove
+```
+    
+### 逆トラバース
+
+```text
+ReverseTraversal(tail)
+  Pre: tail is the node of the list to traverse
+  Post: the list has been traversed in reverse order
+  n ← tail
+  while n = ø
+    yield n.value
+    n ← n.previous
+  end while
+end Reverse Traversal
+```
+    
+## 計算量
+
+## 時間計算量
+
+| Access    | Search    | Insertion | Deletion  |
+| :-------: | :-------: | :-------: | :-------: |
+| O(n)      | O(n)      | O(1)      | O(n)      |
+
+### 空間計算量
+
+O(n)
+
+## 参考
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Doubly_linked_list)
+- [YouTube](https://www.youtube.com/watch?v=JdQeNxWCguQ&t=7s&index=72&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
--- a/src/data-structures/doubly-linked-list/README.md
+++ b/src/data-structures/doubly-linked-list/README.md
@ -1,8 +1,10 @@
 # Doubly Linked List

 _Read this in other languages:_
+[_Русский_](README.ru-RU.md),
 [_简体中文_](README.zh-CN.md),
-[_Русский_](README.ru-RU.md)
+[_日本語_](README.ja-JP.md),
+[_Português_](README.pt-BR.md)

 In computer science, a **doubly linked list** is a linked data structure that 
 consists of a set of sequentially linked records called nodes. Each node contains 
@ -58,13 +60,13 @@ Remove(head, value)
      head ← ø
      tail ← ø
    else
-      head ← head.Next
+      head ← head.next
      head.previous ← ø
    end if
    return true
  end if
  n ← head.next
-  while n = ø and value = n.value
+  while n = ø and value !== n.value
    n ← n.next
  end while
  if n = tail
@ -100,7 +102,7 @@ end Reverse Traversal

 | Access    | Search    | Insertion | Deletion  |
 | :-------: | :-------: | :-------: | :-------: |
-| O(n)      | O(n)      | O(1)      | O(1)      |
+| O(n)      | O(n)      | O(1)      | O(n)      |

 ### Space Complexity

--- a/src/data-structures/doubly-linked-list/README.pt-BR.md
+++ b/src/data-structures/doubly-linked-list/README.pt-BR.md
@ -0,0 +1,111 @@
+# Lista Duplamente Ligada (Doubly Linked List)
+
+Na ciência da computação, uma **lista duplamente conectada** é uma estrutura
+de dados vinculada que se consistem em um conjunto de registros
+sequencialmente vinculados chamados de nós (nodes). Em cada nó contém dois
+campos, chamados de ligações, que são referenciados ao nó anterior e posterior
+de uma sequência de nós. O começo e o fim dos nós anteriormente e posteiormente
+ligados, respectiviamente, apontam para algum tipo de terminação, normalmente
+um nó sentinela ou nulo, para facilitar a travessia da lista. Se existe
+somente um nó sentinela, então a lista é ligada circularmente através do nó
+sentinela. Ela pode ser conceitualizada como duas listas individualmente ligadas
+e formadas a partir dos mesmos itens, mas em ordem sequencial opostas.
+
+![Doubly Linked List](https://upload.wikimedia.org/wikipedia/commons/5/5e/Doubly-linked-list.svg)
+
+Os dois nós ligados permitem a travessia da lista em qualquer direção.
+Enquanto adicionar ou remover um nó de uma lista duplamente vinculada requer
+alterar mais ligações (conexões) do que em uma lista encadeada individualmente
+(singly linked list), as operações são mais simples e potencialmente mais
+eficientes (para nós que não sejam nós iniciais) porque não há necessidade
+de se manter rastreamento do nó anterior durante a travessia ou não há
+necessidade de percorrer a lista para encontrar o nó anterior, para que
+então sua ligação/conexão possa ser modificada.
+
+## Pseudocódigo para Operações Básicas
+
+### Inserir
+
+```text
+Add(value)
+  Pre: value is the value to add to the list
+  Post: value has been placed at the tail of the list
+  n ← node(value)
+  if head = ø
+    head ← n
+    tail ← n
+  else
+    n.previous ← tail
+    tail.next ← n
+    tail ← n
+  end if
+end Add
+```
+    
+### Deletar
+
+```text
+Remove(head, value)
+  Pre: head is the head node in the list
+       value is the value to remove from the list
+  Post: value is removed from the list, true; otherwise false
+  if head = ø
+    return false
+  end if
+  if value = head.value
+    if head = tail
+      head ← ø
+      tail ← ø
+    else
+      head ← head.next
+      head.previous ← ø
+    end if
+    return true
+  end if
+  n ← head.next
+  while n = ø and value !== n.value
+    n ← n.next
+  end while
+  if n = tail
+    tail ← tail.previous
+    tail.next ← ø
+    return true
+  else if n = ø
+    n.previous.next ← n.next
+    n.next.previous ← n.previous
+    return true
+  end if
+  return false
+end Remove
+```
+    
+### Travessia reversa
+
+```text
+ReverseTraversal(tail)
+  Pre: tail is the node of the list to traverse
+  Post: the list has been traversed in reverse order
+  n ← tail
+  while n = ø
+    yield n.value
+    n ← n.previous
+  end while
+end Reverse Traversal
+```
+    
+## Complexidades
+
+## Complexidade de Tempo
+
+| Acesso    | Pesquisa    | Inserção | Remoção  |
+| :-------: | :---------: | :------: | :------: |
+| O(n)      | O(n)        | O(1)     | O(n)     |
+
+### Complexidade de Espaço
+
+O(n)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Doubly_linked_list)
+- [YouTube](https://www.youtube.com/watch?v=JdQeNxWCguQ&t=7s&index=72&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
--- a/src/data-structures/doubly-linked-list/README.ru-RU.md
+++ b/src/data-structures/doubly-linked-list/README.ru-RU.md
@ -54,7 +54,7 @@ Remove(head, value)
      head ← ø
      tail ← ø
    else
-      head ← head.Next
+      head ← head.next
      head.previous ← ø
    end if
    return true
--- a/src/data-structures/doubly-linked-list/README.zh-CN.md
+++ b/src/data-structures/doubly-linked-list/README.zh-CN.md
@ -45,7 +45,7 @@ Remove(head, value)
      head ← ø
      tail ← ø
    else
-      head ← head.Next
+      head ← head.next
      head.previous ← ø
    end if
    return true
--- a/src/data-structures/graph/README.md
+++ b/src/data-structures/graph/README.md
@ -1,5 +1,10 @@
 # Graph

+_Read this in other languages:_
+[_简体中文_](README.zh-CN.md),
+[_Русский_](README.ru-RU.md),
+[_Português_](README.pt-BR.md)
+
 In computer science, a **graph** is an abstract data type 
 that is meant to implement the undirected graph and 
 directed graph concepts from mathematics, specifically
--- a/src/data-structures/graph/README.pt-BR.md
+++ b/src/data-structures/graph/README.pt-BR.md
@ -0,0 +1,26 @@
+# Gráfico (Graph)
+
+Na ciência da computação, um **gráfico** é uma abstração de estrutura
+de dados que se destina a implementar os conceitos da matemática de
+gráficos direcionados e não direcionados, especificamente o campo da
+teoria dos gráficos.
+
+Uma estrutura de dados gráficos consiste em um finito (e possivelmente
+mutável) conjunto de vértices, nós ou pontos, juntos com um
+conjunto de pares não ordenados desses vértices para um gráfico não
+direcionado ou para um conjunto de pares ordenados para um gráfico
+direcionado. Esses pares são conhecidos como arestas, arcos
+ou linhas diretas para um gráfico não direcionado e como setas,
+arestas direcionadas, arcos direcionados ou linhas direcionadas
+para um gráfico direcionado.
+
+Os vértices podem fazer parte a estrutura do gráfico, ou podem
+ser entidades externas representadas por índices inteiros ou referências.
+
+![Graph](https://www.tutorialspoint.com/data_structures_algorithms/images/graph.jpg)
+
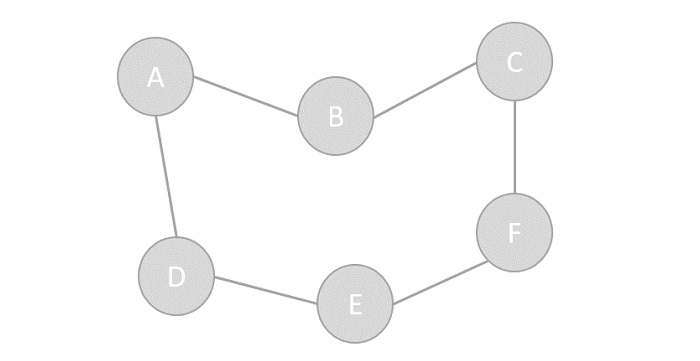
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Graph_(abstract_data_type))
+- [Introduction to Graphs on YouTube](https://www.youtube.com/watch?v=gXgEDyodOJU&index=9&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+- [Graphs representation on YouTube](https://www.youtube.com/watch?v=k1wraWzqtvQ&index=10&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
--- a/src/data-structures/graph/README.ru-RU.md
+++ b/src/data-structures/graph/README.ru-RU.md
@ -0,0 +1,24 @@
+# Граф
+
+**Граф** в информатике - абстрактный тип данных, который должен реализовывать концепции направленного и ненаправленного
+графа в математике, особенно в области теории графов.
+
+Структура данных графа состоит из конечного (и возможно изменяющегося) набора вершин или узлов, или точек, совместно с 
+набором ненаправленных пар этих вершин для ненаправленного графа или с набором направленных пар для направленного графа.
+Эти пары известны как рёбра, арки или линии для ненаправленного графа и как стрелки, направленные рёбра, направленные
+арки или направленные линии для направленного графа. Эти вершины могут быть частью структуры графа, или внешними
+сущностями, представленными целочисленными индексами или ссылками.
+
+Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и
+дополнительными данными о вершинах или рёбрах. Многие структуры, представляющие практический интерес в математике и
+информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи
+ориентированного графа, в котором вершины — это статьи, а дуги (ориентированные рёбра) — гиперссылки.
+
+![Граф](https://www.tutorialspoint.com/data_structures_algorithms/images/graph.jpg)
+
+## Ссылки
+
+- [Граф в математике на Wikipedia](https://ru.wikipedia.org/wiki/%D0%93%D1%80%D0%B0%D1%84_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0))
+- [Графы на YouTube. Часть 1(~10 мин)](https://www.youtube.com/watch?v=GOUuhJPLG3s)
+- [Графы на YouTube. Часть 2(~10 мин)](https://www.youtube.com/watch?v=N-kCJJkTk7g)
+- [Графы на YouTube. Часть 3(~10 мин)](https://www.youtube.com/watch?v=2o3TINew0b8)
--- a/src/data-structures/hash-table/README.ja-JP.md
+++ b/src/data-structures/hash-table/README.ja-JP.md
@ -0,0 +1,16 @@
+# ハッシュテーブル
+ 
+コンピュータサイエンスにおいて、**ハッシュテーブル**（ハッシュマップ)は*キーを値にマッピング*できる*連想配列*の機能を持ったデータ構造です。ハッシュテーブルは*ハッシュ関数*を使ってバケットやスロットの配列へのインデックスを計算し、そこから目的の値を見つけることができます。
+
+理想的には、ハッシュ関数は各キーを一意のバケットに割り当てますが、ほとんどのハッシュテーブルは不完全なハッシュ関数を採用しているため、複数のキーに対して同じインデックスを生成した時にハッシュの衝突が起こります。このような衝突は何らかの方法で対処する必要があります。
+
+![Hash Table](https://upload.wikimedia.org/wikipedia/commons/7/7d/Hash_table_3_1_1_0_1_0_0_SP.svg)
+
+チェイン法によるハッシュの衝突の解決例
+
+![Hash Collision](https://upload.wikimedia.org/wikipedia/commons/d/d0/Hash_table_5_0_1_1_1_1_1_LL.svg)
+
+## 参考
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Hash_table)
+- [YouTube](https://www.youtube.com/watch?v=shs0KM3wKv8&index=4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
--- a/src/data-structures/hash-table/README.md
+++ b/src/data-structures/hash-table/README.md
@ -1,5 +1,11 @@
 # Hash Table

+_Read this in other languages:_
+[_简体中文_](README.zh-CN.md),
+[_Русский_](README.ru-RU.md),
+[_日本語_](README.ja-JP.md),
+[_Português_](README.pt-BR.md)
+ 
 In computing, a **hash table** (hash map) is a data 
 structure which implements an *associative array* 
 abstract data type, a structure that can *map keys 
--- a/src/data-structures/hash-table/README.pt-BR.md
+++ b/src/data-structures/hash-table/README.pt-BR.md
@ -0,0 +1,25 @@
+# Tabela de Hash (Hash Table)
+
+Na ciência da computação, uma **tabela de hash** (hash map) é uma
+estrutura de dados pela qual implementa um tipo de dado abstrado de
+*array associativo*, uma estrutura que pode *mapear chaves para valores*.
+Uma tabela de hash utiliza uma *função de hash* para calcular um índice
+em um _array_ de buckets ou slots, a partir do qual o valor desejado
+pode ser encontrado.
+
+Idealmente, a função de hash irá atribuir a cada chave a um bucket único,
+mas a maioria dos designs de tabela de hash emprega uma função de hash
+imperfeita, pela qual poderá causar colisões de hashes onde a função de hash
+gera o mesmo índice para mais de uma chave.Tais colisões devem ser
+acomodados de alguma forma.
+
+![Hash Table](https://upload.wikimedia.org/wikipedia/commons/7/7d/Hash_table_3_1_1_0_1_0_0_SP.svg)
+
+Colisão de hash resolvida por encadeamento separado.
+
+![Hash Collision](https://upload.wikimedia.org/wikipedia/commons/d/d0/Hash_table_5_0_1_1_1_1_1_LL.svg)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Hash_table)
+- [YouTube](https://www.youtube.com/watch?v=shs0KM3wKv8&index=4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
--- a/src/data-structures/hash-table/README.ru-RU.md
+++ b/src/data-structures/hash-table/README.ru-RU.md
@ -0,0 +1,25 @@
+# Хэш таблица
+
+**Хеш-таблица** - структура данных, реализующая абстрактный тип данных *ассоциативный массив*, т.е. структура, которая
+*связывает ключи со значениями*. Хеш-таблица использует *хеш-функцию* для вычисления индекса в массиве, в котором может
+быть найдено желаемое значение. Ниже представлена хеш-таблица, в которой ключём выступает имя человека, а значениями 
+являются телефонные номера. Хеш-функция преобразует ключ-имя в индекс массива с телефонными номерами.
+
+![Хеш-таблица](https://upload.wikimedia.org/wikipedia/commons/7/7d/Hash_table_3_1_1_0_1_0_0_SP.svg)
+
+В идеале хеш-функция будет присваивать элементу массива уникальный ключ. Однако большинство реальных хеш-таблиц
+используют несовершенные хеш-функции. Это может привести к ситуациям, когда хеш-функция генерирует одинаковый индекс для
+нескольких ключей. Данные ситуации называются коллизиями и должны быть как-то разрешены.
+
+Существует два варианта решения коллизий - хеш-таблица с цепочками и с открытой адресацией.
+
+Метод цепочек подразумевает хранение значений, соответствующих одному и тому же индексу в виде связного списка(цепочки).
+![Хеш цепочки](https://upload.wikimedia.org/wikipedia/commons/d/d0/Hash_table_5_0_1_1_1_1_1_LL.svg)
+
+Метод открытой адресации помещает значение, для которого получен дублирующий индекс, в первую свободную ячейку.
+![Хеш открытая адресация](https://upload.wikimedia.org/wikipedia/commons/thumb/b/bf/Hash_table_5_0_1_1_1_1_0_SP.svg/380px-Hash_table_5_0_1_1_1_1_0_SP.svg.png)
+
+## Ссылки
+
+- [Wikipedia](https://ru.wikipedia.org/wiki/%D0%A5%D0%B5%D1%88-%D1%82%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B0)
+- [YouTube](https://www.youtube.com/watch?v=rVr1y32fDI0)
--- a/src/data-structures/heap/README.ja-JP.md
+++ b/src/data-structures/heap/README.ja-JP.md
@ -0,0 +1,18 @@
+# ヒープ (データ構造)
+
+コンピュータサイエンスにおいて、*ヒープ*は特殊な木構造のデータ構造で、後述するヒープの特性を持っています。
+
+*最小ヒープ*では、もし`P`が`C`の親ノードの場合、`P`のキー(値)は`C`のキーより小さい、または等しくなります。
+
+![MinHeap](https://upload.wikimedia.org/wikipedia/commons/6/69/Min-heap.png)
+
+*最大ヒープ*では、`P`のキーは`C`のキーより大きい、もしくは等しくなります。
+
+![Heap](https://upload.wikimedia.org/wikipedia/commons/3/38/Max-Heap.svg)
+
+ヒープの「トップ」のノードには親ノードが存在せず、ルートノードと呼ばれます。
+
+## 参考
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Heap_(data_structure))
+- [YouTube](https://www.youtube.com/watch?v=t0Cq6tVNRBA&index=5&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
--- a/src/data-structures/heap/README.md
+++ b/src/data-structures/heap/README.md
@ -1,5 +1,11 @@
 # Heap (data-structure)

+_Read this in other languages:_
+[_简体中文_](README.zh-CN.md),
+[_Русский_](README.ru-RU.md),
+[_日本語_](README.ja-JP.md),
+[_Português_](README.pt-BR.md)
+
 In computer science, a **heap** is a specialized tree-based 
 data structure that satisfies the heap property described
 below.
--- a/src/data-structures/heap/README.pt-BR.md
+++ b/src/data-structures/heap/README.pt-BR.md
@ -0,0 +1,21 @@
+# Heap (estrutura de dados)
+
+Na ciência da computação, um **heap** é uma estrutura de dados
+baseada em uma árvore especializada que satisfaz a propriedade _heap_ descrita abaixo.
+
+Em um *heap mínimo* (min heap), caso `P` é um nó pai de `C`, então a chave
+(o valor) de `P` é menor ou igual a chave de `C`.
+
+![MinHeap](https://upload.wikimedia.org/wikipedia/commons/6/69/Min-heap.png)
+
+Em uma *heap máximo* (max heap), a chave de `P` é maior ou igual
+a chave de `C`.
+
+![Heap](https://upload.wikimedia.org/wikipedia/commons/3/38/Max-Heap.svg)
+
+O nó no "topo" do _heap_, cujo não possui pais, é chamado de nó raiz.
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Heap_(data_structure))
+- [YouTube](https://www.youtube.com/watch?v=t0Cq6tVNRBA&index=5&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
--- a/src/data-structures/heap/README.ru-RU.md
+++ b/src/data-structures/heap/README.ru-RU.md
@ -0,0 +1,22 @@
+# Куча (структура данных)
+
+В компьютерных науках куча — это специализированная структура данных типа дерево, которая удовлетворяет свойству кучи:
+если B является узлом-потомком узла A, то ключ(A) ≥ ключ(B). Из этого следует, что элемент с наибольшим ключом всегда
+является корневым узлом кучи, поэтому иногда такие кучи называют max-кучами.
+
+![Max-куча](https://upload.wikimedia.org/wikipedia/commons/3/38/Max-Heap.svg)
+
+Если сравнение перевернуть, то наименьший элемент будет всегда корневым узлом, такие кучи называют min-кучами.
+
+![Min-куча](https://upload.wikimedia.org/wikipedia/commons/6/69/Min-heap.png)
+
+Не существует никаких ограничений относительно того, сколько узлов-потомков имеет каждый узел кучи. На практике их
+число обычно не более двух. Куча является максимально эффективной реализацией абстрактного типа данных, который
+называется очередью с приоритетом.
+
+Узел на вершине кучи, у которого нет родителей, называется корневым узлом.
+
+## Ссылки
+
+- [Wikipedia](https://ru.wikipedia.org/wiki/Куча_(структура_данных))
+- [YouTube](https://www.youtube.com/watch?v=noQ4SUoqrQA)
--- a/src/data-structures/linked-list/README.ja-JP.md
+++ b/src/data-structures/linked-list/README.ja-JP.md
@ -0,0 +1,141 @@
+# リンクリスト
+
+コンピュータサイエンスにおいて、**リンクリスト**はデータ要素の線形コレクションです。要素の順番はメモリ内の物理的な配置によっては決まりません。代わりに、各要素が次の要素を指しています。リンクリストはノードのグループからなるデータ構造です。最も単純な形式では、各ノードはデータとシーケンス内における次のノードへの参照(つまり、リンク)で構成されています。この構造はイテレーションにおいて任意の位置へ要素を効率的に挿入、削除することを可能にしています。より複雑なリンクリストではリンクをさらに追加することで、任意の要素の参照から要素を効率的に挿入、削除することを可能にしています。リンクリストの欠点はアクセスタイムが線形である(そして、パイプライン処理が難しい)ことです。ランダムアクセスのような高速なアクセスは実現不可能です。配列の方がリンクリストと比較して参照の局所性が優れています。
+
+![Linked List](https://upload.wikimedia.org/wikipedia/commons/6/6d/Singly-linked-list.svg)
+
+## 基本操作の擬似コード
+
+### 挿入
+
+```text
+Add(value)
+  Pre: value is the value to add to the list
+  Post: value has been placed at the tail of the list
+  n ← node(value)
+  if head = ø
+    head ← n
+    tail ← n
+  else
+    tail.next ← n
+    tail ← n
+  end if
+end Add
+```
+
+```text
+Prepend(value)
+ Pre: value is the value to add to the list
+ Post: value has been placed at the head of the list
+ n ← node(value)
+ n.next ← head
+ head ← n
+ if tail = ø
+   tail ← n
+ end
+end Prepend
+```
+
+### 検索
+
+```text
+Contains(head, value)
+  Pre: head is the head node in the list
+       value is the value to search for
+  Post: the item is either in the linked list, true; otherwise false
+  n ← head
+  while n != ø and n.value != value
+    n ← n.next
+  end while
+  if n = ø
+    return false
+  end if
+  return true
+end Contains
+```
+    
+### 削除
+
+```text
+Remove(head, value)
+  Pre: head is the head node in the list
+       value is the value to remove from the list
+  Post: value is removed from the list, true, otherwise false
+  if head = ø
+    return false
+  end if
+  n ← head
+  if n.value = value
+    if head = tail
+      head ← ø
+      tail ← ø
+    else
+      head ← head.next
+    end if
+    return true
+  end if
+  while n.next != ø and n.next.value != value
+    n ← n.next
+  end while
+  if n.next != ø
+    if n.next = tail
+      tail ← n
+    end if
+    n.next ← n.next.next
+    return true
+  end if
+  return false
+end Remove
+```
+
+### トラバース
+
+```text
+Traverse(head)
+  Pre: head is the head node in the list
+  Post: the items in the list have been traversed
+  n ← head
+  while n != ø
+    yield n.value
+    n ← n.next
+  end while
+end Traverse
+```
+
+### 逆トラバース
+
+```text
+ReverseTraversal(head, tail)
+  Pre: head and tail belong to the same list
+  Post: the items in the list have been traversed in reverse order
+  if tail != ø
+    curr ← tail
+    while curr != head
+      prev ← head
+      while prev.next != curr
+        prev ← prev.next
+      end while
+      yield curr.value
+      curr ← prev
+    end while
+   yield curr.value
+  end if
+end ReverseTraversal
+```
+
+## 計算量
+
+### 時間計算量
+
+| Access    | Search    | Insertion | Deletion  |
+| :-------: | :-------: | :-------: | :-------: |
+| O(n)      | O(n)      | O(1)      | O(n)      |
+
+### 空間計算量
+
+O(n)
+
+## 参考
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Linked_list)
+- [YouTube](https://www.youtube.com/watch?v=njTh_OwMljA&index=2&t=1s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
--- a/src/data-structures/linked-list/README.md
+++ b/src/data-structures/linked-list/README.md
@ -2,7 +2,9 @@

 _Read this in other languages:_
 [_简体中文_](README.zh-CN.md),
-[_Русский_](README.ru-RU.md)
+[_Русский_](README.ru-RU.md),
+[_日本語_](README.ja-JP.md),
+[_Português_](README.pt-BR.md)

 In computer science, a **linked list** is a linear collection 
 of data elements, in which linear order is not given by 
@ -137,7 +139,7 @@ ReverseTraversal(head, tail)
      yield curr.value
      curr ← prev
    end while
-   yeild curr.value
+   yield curr.value
  end if
 end ReverseTraversal
 ```
@ -148,7 +150,7 @@ end ReverseTraversal

 | Access    | Search    | Insertion | Deletion  |
 | :-------: | :-------: | :-------: | :-------: |
-| O(n)      | O(n)      | O(1)      | O(1)      |
+| O(n)      | O(n)      | O(1)      | O(n)      |

 ### Space Complexity

--- a/src/data-structures/linked-list/README.pt-BR.md
+++ b/src/data-structures/linked-list/README.pt-BR.md
@ -0,0 +1,157 @@
+# Lista Encadeada (Linked List)
+
+Na ciência da computação, uma **lista encadeada** é uma coleção linear de
+elementos de dado, em que a ordem linear não é dada por sua locação
+física na memória. Em vez disso, cada elemento aponta para o próximo.
+É uma estrutura de dados consistindo em um grupo de nós
+que juntos representam uma sequência. Sob a forma mais simples,
+cada nó é composto de dados e uma referência (em outras palavras,
+uma ligação/conexão) para o próximo nó na sequência. Esta estrutua
+permite uma eficiente inserção e remoção de elementos de qualquer
+posição na sequência durante a iteração.
+
+Variantes mais complexas adicionam ligações adicionais, permitindo
+uma inserção ou remoção mais eficiente a partir de referências
+de elementos arbitrárias. Uma desvantagem das listas vinculadas
+é que o tempo de acesso é linear (e difícil de inserir em uma
+pipeline). Acessos mais rápidos, como acesso aleatório, não é viável.
+Arrays possuem uma melhor localização de cache em comparação
+com lista encadeada (linked list).
+
+![Linked List](https://upload.wikimedia.org/wikipedia/commons/6/6d/Singly-linked-list.svg)
+
+## Pseudo código para Operações Básicas
+
+### Inserção
+
+```text
+Add(value)
+  Pre: value is the value to add to the list
+  Post: value has been placed at the tail of the list
+  n ← node(value)
+  if head = ø
+    head ← n
+    tail ← n
+  else
+    tail.next ← n
+    tail ← n
+  end if
+end Add
+```
+
+```text
+Prepend(value)
+ Pre: value is the value to add to the list
+ Post: value has been placed at the head of the list
+ n ← node(value)
+ n.next ← head
+ head ← n
+ if tail = ø
+   tail ← n
+ end
+end Prepend
+```
+
+### Pesquisa
+
+```text
+Contains(head, value)
+  Pre: head is the head node in the list
+       value is the value to search for
+  Post: the item is either in the linked list, true; otherwise false
+  n ← head
+  while n != ø and n.value != value
+    n ← n.next
+  end while
+  if n = ø
+    return false
+  end if
+  return true
+end Contains
+```
+
+### Remoção
+
+```text
+Remove(head, value)
+  Pre: head is the head node in the list
+       value is the value to remove from the list
+  Post: value is removed from the list, true, otherwise false
+  if head = ø
+    return false
+  end if
+  n ← head
+  if n.value = value
+    if head = tail
+      head ← ø
+      tail ← ø
+    else
+      head ← head.next
+    end if
+    return true
+  end if
+  while n.next != ø and n.next.value != value
+    n ← n.next
+  end while
+  if n.next != ø
+    if n.next = tail
+      tail ← n
+    end if
+    n.next ← n.next.next
+    return true
+  end if
+  return false
+end Remove
+```
+
+### Travessia
+
+```text
+Traverse(head)
+  Pre: head is the head node in the list
+  Post: the items in the list have been traversed
+  n ← head
+  while n != ø
+    yield n.value
+    n ← n.next
+  end while
+end Traverse
+```
+
+### Travessia Reversa
+
+```text
+ReverseTraversal(head, tail)
+  Pre: head and tail belong to the same list
+  Post: the items in the list have been traversed in reverse order
+  if tail != ø
+    curr ← tail
+    while curr != head
+      prev ← head
+      while prev.next != curr
+        prev ← prev.next
+      end while
+      yield curr.value
+      curr ← prev
+    end while
+   yield curr.value
+  end if
+end ReverseTraversal
+```
+
+## Complexidades
+
+### Complexidade de Tempo
+
+| Acesso | Pesquisa | Inserção | Remoção |
+| :----: | :------: | :------: | :-----: |
+|  O(n)  |  O(n)    |  O(1)    |  O(n)   |
+
+### Complexidade de Espaçø
+
+O(n)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Linked_list)
+- [YouTube](https://www.youtube.com/watch?v=njTh_OwMljA&index=2&t=1s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
--- a/src/data-structures/linked-list/README.ru-RU.md
+++ b/src/data-structures/linked-list/README.ru-RU.md
@ -122,7 +122,7 @@ ReverseTraversal(head, tail)
      yield curr.value
      curr ← prev
    end while
-   yeild curr.value
+   yield curr.value
  end if
 end ReverseTraversal
 ```
--- a/src/data-structures/linked-list/README.zh-CN.md
+++ b/src/data-structures/linked-list/README.zh-CN.md
@ -124,7 +124,7 @@ ReverseTraversal(head, tail)
      yield curr.value
      curr ← prev
    end while
-   yeild curr.value
+   yield curr.value
  end if
 end ReverseTraversal
 ```
--- a/src/data-structures/priority-queue/PriorityQueue.js
+++ b/src/data-structures/priority-queue/PriorityQueue.js
@ -1,52 +1,59 @@
 import MinHeap from '../heap/MinHeap';
 import Comparator from '../../utils/comparator/Comparator';

-// It is the same as min heap except that when comparing to elements
-// we take into account not element's value but rather its priority.
+// It is the same as min heap except that when comparing two elements
+// we take into account its priority instead of the element's value.
 export default class PriorityQueue extends MinHeap {
  constructor() {
+    // Call MinHip constructor first.
    super();
-    this.priorities = {};
+
+    // Setup priorities map.
+    this.priorities = new Map();
+
+    // Use custom comparator for heap elements that will take element priority
+    // instead of element value into account.
    this.compare = new Comparator(this.comparePriority.bind(this));
  }

  /**
-   * @param {*} item
-   * @param {number} [priority]
+   * Add item to the priority queue.
+   * @param {*} item - item we're going to add to the queue.
+   * @param {number} [priority] - items priority.
   * @return {PriorityQueue}
   */
  add(item, priority = 0) {
-    this.priorities[item] = priority;
+    this.priorities.set(item, priority);
    super.add(item);
-
    return this;
  }

  /**
-   * @param {*} item
-   * @param {Comparator} [customFindingComparator]
+   * Remove item from priority queue.
+   * @param {*} item - item we're going to remove.
+   * @param {Comparator} [customFindingComparator] - custom function for finding the item to remove
   * @return {PriorityQueue}
   */
  remove(item, customFindingComparator) {
    super.remove(item, customFindingComparator);
-    delete this.priorities[item];
-
+    this.priorities.delete(item);
    return this;
  }

  /**
-   * @param {*} item
-   * @param {number} priority
+   * Change priority of the item in a queue.
+   * @param {*} item - item we're going to re-prioritize.
+   * @param {number} priority - new item's priority.
   * @return {PriorityQueue}
   */
  changePriority(item, priority) {
    this.remove(item, new Comparator(this.compareValue));
    this.add(item, priority);
-
    return this;
  }

  /**
+   * Find item by ite value.
   * @param {*} item
   * @return {Number[]}
   */
@ -55,6 +62,7 @@ export default class PriorityQueue extends MinHeap {
  }

  /**
+   * Check if item already exists in a queue.
   * @param {*} item
   * @return {boolean}
   */
@ -63,19 +71,20 @@ export default class PriorityQueue extends MinHeap {
  }

  /**
+   * Compares priorities of two items.
   * @param {*} a
   * @param {*} b
   * @return {number}
   */
  comparePriority(a, b) {
-    if (this.priorities[a] === this.priorities[b]) {
+    if (this.priorities.get(a) === this.priorities.get(b)) {
      return 0;
    }
-
-    return this.priorities[a] < this.priorities[b] ? -1 : 1;
+    return this.priorities.get(a) < this.priorities.get(b) ? -1 : 1;
  }

  /**
+   * Compares values of two items.
   * @param {*} a
   * @param {*} b
   * @return {number}
@ -84,7 +93,6 @@ export default class PriorityQueue extends MinHeap {
    if (a === b) {
      return 0;
    }
-
    return a < b ? -1 : 1;
  }
 }
--- a/src/data-structures/priority-queue/README.ja-JP.md
+++ b/src/data-structures/priority-queue/README.ja-JP.md
@ -0,0 +1,10 @@
+# 優先度付きキュー
+
+コンピュータサイエンスにおいて、**優先度付きキュー**は通常のキューやスタックのデータ構造と似た抽象データ型ですが、各要素に「優先度」が関連づけられています。優先度付きキューでは優先度の高い要素が優先度の低い要素よりも先に処理されます。もし2つの要素が同じ優先度だった場合、それらはキュー内の順序に従って処理されます。
+
+優先度付きキューは多くの場合ヒープによって実装されていますが、概念的にはヒープとは異なります。優先度付きキューは「リスト」や「マップ」のような抽象的な概念です。リストがリンクリストや配列で実装できるのと同様に、優先度付きキューはヒープや未ソート配列のような様々な方法で実装することができます。
+
+## 参考
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Priority_queue)
+- [YouTube](https://www.youtube.com/watch?v=wptevk0bshY&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=6)
--- a/src/data-structures/priority-queue/README.md
+++ b/src/data-structures/priority-queue/README.md
@ -2,7 +2,9 @@

 _Read this in other languages:_
 [_简体中文_](README.zh-CN.md),
-[_Русский_](README.ru-RU.md)
+[_Русский_](README.ru-RU.md),
+[_日本語_](README.ja-JP.md),
+[_Português_](README.pt-BR.md)

 In computer science, a **priority queue** is an abstract data type 
 which is like a regular queue or stack data structure, but where 
--- a/src/data-structures/priority-queue/README.pt-BR.md
+++ b/src/data-structures/priority-queue/README.pt-BR.md
@ -0,0 +1,23 @@
+# Fila de Prioridade (Priority Queue)
+
+Na ciência da computação, uma **fila de prioridade** é um tipo de dados
+abastrato que é como uma fila regular (regular queue) ou estrutura de
+dados de pilha (stack), mas adicionalmente cada elemento possui uma
+"prioridade" associada.
+
+Em uma fila de prioridade, um elemento com uma prioridade alta é servido
+antes de um elemento com baixa prioridade. Caso dois elementos posusam a
+mesma prioridade, eles serão servidos de acordo com sua ordem na fila.
+
+Enquanto as filas de prioridade são frequentemente implementadas com
+pilhas (heaps), elas são conceitualmente distintas das pilhas (heaps).
+A fila de prioridade é um conceito abstrato como uma "lista" (list) ou
+um "mapa" (map); assim como uma lista pode ser implementada com uma
+lista encadeada (liked list) ou um array, a fila de prioridade pode ser
+implementada com uma pilha (heap) ou com uima variedade de outros métodos,
+como um array não ordenado (unordered array).
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Priority_queue)
+- [YouTube](https://www.youtube.com/watch?v=wptevk0bshY&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=6)
--- a/src/data-structures/priority-queue/test/PriorityQueue.test.js
+++ b/src/data-structures/priority-queue/test/PriorityQueue.test.js
@ -20,6 +20,23 @@ describe('PriorityQueue', () => {
    expect(priorityQueue.peek()).toBe(100);
  });

+  it('should be possible to use objects in priority queue', () => {
+    const priorityQueue = new PriorityQueue();
+
+    const user1 = { name: 'Mike' };
+    const user2 = { name: 'Bill' };
+    const user3 = { name: 'Jane' };
+
+    priorityQueue.add(user1, 1);
+    expect(priorityQueue.peek()).toBe(user1);
+
+    priorityQueue.add(user2, 2);
+    expect(priorityQueue.peek()).toBe(user1);
+
+    priorityQueue.add(user3, 0);
+    expect(priorityQueue.peek()).toBe(user3);
+  });
+
  it('should poll from queue with respect to priorities', () => {
    const priorityQueue = new PriorityQueue();

@ -34,7 +51,7 @@ describe('PriorityQueue', () => {
    expect(priorityQueue.poll()).toBe(5);
  });

-  it('should be possible to change priority of internal nodes', () => {
+  it('should be possible to change priority of head node', () => {
    const priorityQueue = new PriorityQueue();

    priorityQueue.add(10, 1);
@ -42,6 +59,8 @@ describe('PriorityQueue', () => {
    priorityQueue.add(100, 0);
    priorityQueue.add(200, 0);

+    expect(priorityQueue.peek()).toBe(100);
+
    priorityQueue.changePriority(100, 10);
    priorityQueue.changePriority(10, 20);

@ -51,7 +70,7 @@ describe('PriorityQueue', () => {
    expect(priorityQueue.poll()).toBe(10);
  });

-  it('should be possible to change priority of head node', () => {
+  it('should be possible to change priority of internal nodes', () => {
    const priorityQueue = new PriorityQueue();

    priorityQueue.add(10, 1);
@ -59,6 +78,8 @@ describe('PriorityQueue', () => {
    priorityQueue.add(100, 0);
    priorityQueue.add(200, 0);

+    expect(priorityQueue.peek()).toBe(100);
+
    priorityQueue.changePriority(200, 10);
    priorityQueue.changePriority(10, 20);

--- a/src/data-structures/queue/README.ja-JP.md
+++ b/src/data-structures/queue/README.ja-JP.md
@ -0,0 +1,12 @@
+# キュー
+
+コンピュータサイエンスにおいて、**キュー**は特定の種類の抽象データ型またはコレクションです。コレクションの中のエンティティは順番に並べられており、コレクションに対する基本的な（または唯一の)操作は末尾にエンティティを追加するエンキューと、先頭からエンティティを削除するデキューがあります。これにより、キューは先入れ先出し(FIFO)のデータ構造となります。FIFOのデータ構造では、キューに追加された最初の要素が最初に削除されます。これは、新しい要素が追加されたら、その要素を削除するにはそれまでに追加された全ての要素が削除されなければならないという要件と同じです。多くの場合、ピークのような先頭の要素を検査する操作も備えていて、これはデキューせずに先頭の要素の値を返します。キューは線形のデータ構造や、より抽象的なシーケンシャルなコレクションの一例です。
+
+FIFO(先入れ先出し)のキュー
+
+![Queue](https://upload.wikimedia.org/wikipedia/commons/5/52/Data_Queue.svg)
+
+## 参考
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Queue_(abstract_data_type))
+- [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&)
--- a/src/data-structures/queue/README.md
+++ b/src/data-structures/queue/README.md
@ -2,7 +2,9 @@

 _Read this in other languages:_
 [_简体中文_](README.zh-CN.md),
-[_Русский_](README.ru-RU.md)
+[_Русский_](README.ru-RU.md),
+[_日本語_](README.ja-JP.md),
+[_Português_](README.pt-BR.md)

 In computer science, a **queue** is a particular kind of abstract data 
 type or collection in which the entities in the collection are 
--- a/src/data-structures/queue/README.pt-BR.md
+++ b/src/data-structures/queue/README.pt-BR.md
@ -0,0 +1,28 @@
+# Fila (Queue)
+
+Na ciência da computação, uma **fila** é um tipo particular de abstração
+de tipo de dado ou coleção em que as entidades na coleção são mantidas em
+ordem e a causa primária (ou única) de operações na coleção são a
+adição de entidades à posição final da coleção, conhecido como enfileiramento
+(enqueue) e a remoção de entidades do posição inicial, conhecida como desenfileirar
+(dequeue).Isto torna a fila uma estrutura de dados tipo First-In-First-Out (FIFO).
+
+Em uma estrutura de dados FIFO, o primeiro elemento adicionado a fila
+será o primeiro a ser removido. Isso é equivalente ao requisito em que uma vez
+que um novo elemento é adicionado, todos os elementos que foram adicionados
+anteriormente devem ser removidos antes que o novo elemento possa ser removido.
+
+Muitas vezes uma espiada (peek) ou uma operação de frente é iniciada,
+retornando o valor do elemento da frente, sem desenfileira-lo. Uma lista é
+um exemplo de uma estrutura de dados linear, ou mais abstratamente uma
+coleção seqüencial.
+
+
+Representação de uma file FIFO (first in, first out)
+
+![Queue](https://upload.wikimedia.org/wikipedia/commons/5/52/Data_Queue.svg)
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Queue_(abstract_data_type))
+- [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&)
--- a/src/data-structures/stack/README.ja-JP.md
+++ b/src/data-structures/stack/README.ja-JP.md
@ -0,0 +1,17 @@
+# スタック
+
+コンピュータサイエンスにおいて、**スタック**は抽象データ型で、2つの主要な操作ができる要素のコレクションです。
+
+* **プッシュ**はコレクションに要素を追加します。
+* **ポップ**は最近追加された要素でまだ削除されていないものを削除します。
+
+要素がスタックから外れる順番から、LIFO(後入れ先出し)とも呼ばれます。スタックに変更を加えることなく、先頭の要素を検査するピーク操作を備えることもあります。「スタック」という名前は、物理的な物を上に積み重ねていく様子との類似性に由来しています。一番上の物を取ることは簡単ですが、スタックの下の方にあるものを取るときは先に上にある複数の物を取り除く必要があります。
+
+プッシュとポップの例
+
+![Stack](https://upload.wikimedia.org/wikipedia/commons/b/b4/Lifo_stack.png)
+
+## 参考
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Stack_(abstract_data_type))
+- [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&)
--- a/src/data-structures/stack/README.md
+++ b/src/data-structures/stack/README.md
@ -2,7 +2,9 @@

 _Read this in other languages:_
 [_简体中文_](README.zh-CN.md),
-[_Русский_](README.ru-RU.md)
+[_Русский_](README.ru-RU.md),
+[_日本語_](README.ja-JP.md),
+[_Português_](README.pt-BR.md)

 In computer science, a **stack** is an abstract data type that serves 
 as a collection of elements, with two principal operations:
--- a/src/data-structures/stack/README.pt-BR.md
+++ b/src/data-structures/stack/README.pt-BR.md
@ -0,0 +1,26 @@
+# Stack
+
+Na ciência da computação, um **stack** é uma estrutura de dados abstrata
+que serve como uma coleção de elementos com duas operações principais:
+
+* **push**, pela qual adiciona um elemento à coleção, e
+* **pop**, pela qual remove o último elemento adicionado.
+
+A ordem em que os elementos saem de um _stack_ dá origem ao seu
+nome alternativo, LIFO (last in, first out). Adicionalmente, uma
+espiar a operação pode dar acesso ao topo sem modificar o _stack_.
+O nome "stack" para este tipo de estrutura vem da analogia de
+um conjunto de itens físicos empilhados uns sobre os outros,
+o que facilita retirar um item do topo da pilha, enquanto para chegar a
+um item mais profundo na pilha pode exigir a retirada de
+vários outros itens primeiro.
+
+Representação simples de um tempo de execução de pilha com operações
+_push_ e _pop_.
+
+![Stack](https://upload.wikimedia.org/wikipedia/commons/b/b4/Lifo_stack.png)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Stack_(abstract_data_type))
+- [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&)
--- a/src/data-structures/tree/README.md
+++ b/src/data-structures/tree/README.md
@ -1,5 +1,9 @@
 # Tree

+_Read this in other languages:_
+[_简体中文_](README.zh-CN.md),
+[_Português_](README.pt-BR.md)
+
 * [Binary Search Tree](binary-search-tree)
 * [AVL Tree](avl-tree)
 * [Red-Black Tree](red-black-tree)
--- a/src/data-structures/tree/README.pt-BR.md
+++ b/src/data-structures/tree/README.pt-BR.md
@ -0,0 +1,30 @@
+# Árvore (Tree)
+
+* [Árvore de Pesquisa Binária (Binary Search Tree)](binary-search-tree/README.pt-BR.md)
+* [Árvore AVL (AVL Tree)](avl-tree/README.pt-BR.md)
+* [Árvore Vermelha-Preta (Red-Black Tree)](red-black-tree/README.pt-BR.md)
+* [Árvore de Segmento (Segment Tree)](segment-tree/README.pt-BR.md) - com exemplos de consulta de intervalores min/max/sum
+* [Árvorem Fenwick (Fenwick Tree)](fenwick-tree/README.pt-BR.md) (Árvore Binária Indexada / Binary Indexed Tree)
+
+Na ciência da computação, uma **árvore** é uma estrutura de dados
+abstrada (ADT) amplamente utilizada - ou uma estrutura de dados
+implementando este ADT que simula uma estrutura hierarquica de árvore,
+com valor raíz e sub-árvores de filhos com um nó pai, representado
+como um conjunto de nós conectados.
+
+Uma estrutura de dados em árvore pode ser definida recursivamente como
+(localmente) uma coleção de nós (começando no nó raíz), aonde cada nó
+é uma estrutura de dados consistindo de um valor, junto com uma lista
+de referências aos nós (os "filhos"), com as restrições de que nenhuma
+referência é duplicada e nenhuma aponta para a raiz.
+
+Uma árvore não ordenada simples; neste diagrama, o nó rotulado como `7`
+possui dois filhos, rotulados como `2` e `6`, e um pai, rotulado como `2`.
+O nó raíz, no topo, não possui nenhum pai.
+
+![Tree](https://upload.wikimedia.org/wikipedia/commons/f/f7/Binary_tree.svg)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Tree_(data_structure))
+- [YouTube](https://www.youtube.com/watch?v=oSWTXtMglKE&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=8)
--- a/src/data-structures/tree/avl-tree/README.md
+++ b/src/data-structures/tree/avl-tree/README.md
@ -1,5 +1,8 @@
 # AVL Tree

+_Read this in other languages:_
+[_Português_](README.pt-BR.md)
+
 In computer science, an **AVL tree** (named after inventors 
 Adelson-Velsky and Landis) is a self-balancing binary search 
 tree. It was the first such data structure to be invented. 
--- a/src/data-structures/tree/avl-tree/README.pt-BR.md
+++ b/src/data-structures/tree/avl-tree/README.pt-BR.md
@ -0,0 +1,50 @@
+# Árvore AVL (AVL Tree)
+
+Na ciência da computação, uma **árvore AVL** (em homenagem aos
+inventores Adelson-Velsky e Landis) é uma árvore de pesquisa
+binária auto balanceada. Foi a primeira estrutura de dados a
+ser inventada.
+Em uma árvore AVL, as alturas de duas sub-árvores filhas
+de qualquer nó diferem no máximo em um; se a qualquer momento
+diferirem por em mais de um, um rebalanceamento é feito para
+restaurar esta propriedade.
+Pesquisa, inserção e exclusão possuem tempo `O(log n)` tanto na
+média quanto nos piores casos, onde `n` é o número de nós na
+árvore antes da operação. Inserções e exclusões podem exigir
+que a árvore seja reequilibrada por uma ou mais rotações.
+
+
+Animação mostrando a inserção de vários elementos em uma árvore AVL.
+Inclui as rotações de esquerda, direita, esquerda-direita e direita-esquerda.
+
+![AVL Tree](https://upload.wikimedia.org/wikipedia/commons/f/fd/AVL_Tree_Example.gif)
+
+Árvore AVL com fatores de equilíbrio (verde)
+
+![AVL Tree](https://upload.wikimedia.org/wikipedia/commons/a/ad/AVL-tree-wBalance_K.svg)
+
+### Rotações de Árvores AVL
+
+**Rotação Esquerda-Esquerda**
+
+![Left-Left Rotation](http://btechsmartclass.com/data_structures/ds_images/LL%20Rotation.png)
+
+**Rotação direita-direita**
+
+![Right-Right Rotation](http://btechsmartclass.com/data_structures/ds_images/RR%20Rotation.png)
+
+**Rotação Esquerda-Direita**
+
+![Left-Right Rotation](http://btechsmartclass.com/data_structures/ds_images/LR%20Rotation.png)
+
+**Rotação Direita-Esquerda**
+
+![Right-Right Rotation](http://btechsmartclass.com/data_structures/ds_images/RL%20Rotation.png)
+
+## Referências
+
+* [Wikipedia](https://en.wikipedia.org/wiki/AVL_tree)
+* [Tutorials Point](https://www.tutorialspoint.com/data_structures_algorithms/avl_tree_algorithm.htm)
+* [BTech](http://btechsmartclass.com/data_structures/avl-trees.html)
+* [AVL Tree Insertion on YouTube](https://www.youtube.com/watch?v=rbg7Qf8GkQ4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=12&)
+* [AVL Tree Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/AVLtree.html)
--- a/src/data-structures/tree/binary-search-tree/README.md
+++ b/src/data-structures/tree/binary-search-tree/README.md
@ -1,5 +1,8 @@
 # Binary Search Tree

+_Read this in other languages:_
+[_Português_](README.pt-BR.md)
+
 In computer science, **binary search trees** (BST), sometimes called 
 ordered or sorted binary trees, are a particular type of container: 
 data structures that store "items" (such as numbers, names etc.) 
--- a/src/data-structures/tree/binary-search-tree/README.pt-BR.md
+++ b/src/data-structures/tree/binary-search-tree/README.pt-BR.md
@ -0,0 +1,277 @@
+# Árvore de Pesquisa Binária (Binary Search Tree)
+
+Na ciência da computação **binary search trees** (BST), algumas vezes
+chamadas de árvores binárias ordenadas (_ordered or sorted binary trees_),
+é um tipo particular de container: estruturas de dados que armazenam
+"itens" (como números, nomes, etc.) na memória. Permite pesquisa rápida,
+adição e remoção de itens além de poder ser utilizado para implementar
+tanto conjuntos dinâmicos de itens ou, consultar tabelas que permitem
+encontrar um item por seu valor chave. E.g. encontrar o número de
+telefone de uma pessoa pelo seu nome.
+
+Árvore de Pesquisa Binária mantem seus valores chaves ordenados, para
+que uma pesquisa e outras operações possam usar o princípio da pesquisa
+binária: quando pesquisando por um valor chave na árvore (ou um lugar
+para inserir uma nova chave), eles atravessam a árvore da raiz para a folha,
+fazendo comparações com chaves armazenadas nos nós da árvore e decidindo então,
+com base nas comparações, continuar pesquisando nas sub-árvores a direita ou
+a esquerda. Em média isto significa que cara comparação permite as operações
+pular metade da árvore, para que então, cada pesquisa, inserção ou remoção
+consuma tempo proporcional ao logaritmo do número de itens armazenados na
+árvore. Isto é muito melhor do que um tempo linear necessário para encontrar
+itens por seu valor chave em um array (desorndenado - _unsorted_), mas muito
+mais lento do que operações similares em tableas de hash (_hash tables_).
+
+Uma pesquisa de árvore binária de tamanho 9 e profundidade 3, com valor 8
+na raíz.
+As folhas não foram desenhadas.
+
+
+![Binary Search Tree](https://upload.wikimedia.org/wikipedia/commons/d/da/Binary_search_tree.svg)
+
+## Pseudocódigo para Operações Básicas
+
+### Inserção
+
+```text
+insert(value)
+  Pre: value has passed custom type checks for type T
+  Post: value has been placed in the correct location in the tree
+  if root = ø
+    root ← node(value)
+  else
+    insertNode(root, value)
+  end if
+end insert
+```
+    
+```text
+insertNode(current, value)
+  Pre: current is the node to start from
+  Post: value has been placed in the correct location in the tree
+  if value < current.value
+    if current.left = ø
+      current.left ← node(value)
+    else
+      InsertNode(current.left, value)
+    end if
+  else
+    if current.right = ø
+      current.right ← node(value)
+    else
+      InsertNode(current.right, value)
+    end if
+  end if
+end insertNode
+```
+
+### Pesquisa
+
+```text
+contains(root, value)
+  Pre: root is the root node of the tree, value is what we would like to locate
+  Post: value is either located or not
+  if root = ø
+    return false
+  end if
+  if root.value = value
+    return true
+  else if value < root.value
+    return contains(root.left, value)
+  else
+    return contains(root.right, value)
+  end if
+end contains
+```
+    
+     
+### Remoção
+
+```text
+remove(value)
+  Pre: value is the value of the node to remove, root is the node of the BST
+      count is the number of items in the BST
+  Post: node with value is removed if found in which case yields true, otherwise false
+  nodeToRemove ← findNode(value)
+  if nodeToRemove = ø
+    return false
+  end if
+  parent ← findParent(value)
+  if count = 1
+    root ← ø
+  else if nodeToRemove.left = ø and nodeToRemove.right = ø
+    if nodeToRemove.value < parent.value
+      parent.left ←  nodeToRemove.right
+    else
+      parent.right ← nodeToRemove.right
+    end if
+  else if nodeToRemove.left != ø and nodeToRemove.right != ø
+    next ← nodeToRemove.right
+    while next.left != ø
+      next ← next.left
+    end while
+    if next != nodeToRemove.right
+      remove(next.value)
+      nodeToRemove.value ← next.value
+    else
+      nodeToRemove.value ← next.value
+      nodeToRemove.right ← nodeToRemove.right.right
+    end if
+  else
+    if nodeToRemove.left = ø
+      next ← nodeToRemove.right
+    else
+      next ← nodeToRemove.left
+    end if
+    if root = nodeToRemove
+      root = next
+    else if parent.left = nodeToRemove
+      parent.left = next
+    else if parent.right = nodeToRemove
+      parent.right = next
+    end if
+  end if
+  count ← count - 1
+  return true
+end remove
+```
+
+### Encontrar o Nó Pai
+
+```text
+findParent(value, root)
+  Pre: value is the value of the node we want to find the parent of
+       root is the root node of the BST and is != ø
+  Post: a reference to the prent node of value if found; otherwise ø
+  if value = root.value
+    return ø
+  end if
+  if value < root.value
+    if root.left = ø
+      return ø
+    else if root.left.value = value
+      return root
+    else
+      return findParent(value, root.left)
+    end if
+  else
+    if root.right = ø
+      return ø
+    else if root.right.value = value
+      return root
+    else
+      return findParent(value, root.right)
+    end if
+  end if
+end findParent
+```
+
+### Encontrar um Nó
+
+```text
+findNode(root, value)
+  Pre: value is the value of the node we want to find the parent of
+       root is the root node of the BST
+  Post: a reference to the node of value if found; otherwise ø
+  if root = ø
+    return ø
+  end if
+  if root.value = value
+    return root
+  else if value < root.value
+    return findNode(root.left, value)
+  else
+    return findNode(root.right, value)
+  end if
+end findNode
+```
+    
+### Encontrar Mínimo
+
+```text
+findMin(root)
+  Pre: root is the root node of the BST
+    root = ø
+  Post: the smallest value in the BST is located
+  if root.left = ø
+    return root.value
+  end if
+  findMin(root.left)
+end findMin
+```
+    
+### Encontrar Máximo
+
+```text
+findMax(root)
+  Pre: root is the root node of the BST
+    root = ø
+  Post: the largest value in the BST is located
+  if root.right = ø
+    return root.value
+  end if
+  findMax(root.right)
+end findMax
+```
+    
+### Traversal
+
+#### Na Ordem Traversal (InOrder Traversal)
+
+```text
+inorder(root)
+  Pre: root is the root node of the BST
+  Post: the nodes in the BST have been visited in inorder
+  if root = ø
+    inorder(root.left)
+    yield root.value
+    inorder(root.right)
+  end if
+end inorder
+```
+
+#### Pré Ordem Traversal (PreOrder Traversal)
+
+```text
+preorder(root)
+  Pre: root is the root node of the BST
+  Post: the nodes in the BST have been visited in preorder
+  if root = ø
+    yield root.value
+    preorder(root.left)
+    preorder(root.right)
+  end if
+end preorder
+```
+   
+#### Pós Ordem Traversal (PostOrder Traversal)
+
+```text
+postorder(root)
+  Pre: root is the root node of the BST
+  Post: the nodes in the BST have been visited in postorder
+  if root = ø
+    postorder(root.left)
+    postorder(root.right)
+    yield root.value
+  end if
+end postorder
+```
+     
+## Complexidades
+
+### Complexidade de Tempo
+
+| Access    | Search    | Insertion | Deletion  |
+| :-------: | :-------: | :-------: | :-------: |
+| O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) |
+
+### Complexidade de Espaço
+
+O(n)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Binary_search_tree)
+- [Inserting to BST on YouTube](https://www.youtube.com/watch?v=wcIRPqTR3Kc&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=9&t=0s)
+- [BST Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/BST.html)
--- a/src/data-structures/tree/fenwick-tree/README.md
+++ b/src/data-structures/tree/fenwick-tree/README.md
@ -1,5 +1,8 @@
 # Fenwick Tree / Binary Indexed Tree

+_Read this in other languages:_
+[_Português_](README.pt-BR.md) 
+
 A **Fenwick tree** or **binary indexed tree** is a data 
 structure that can efficiently update elements and 
 calculate prefix sums in a table of numbers.
--- a/src/data-structures/tree/fenwick-tree/README.pt-BR.md
+++ b/src/data-structures/tree/fenwick-tree/README.pt-BR.md
@ -0,0 +1,42 @@
+# Árvore Fenwick / Árvore Binária Indexada (Fenwick Tree / Binary Indexed Tree)
+
+Uma **árvore Fenwick** ou **árvore binária indexada** é um tipo de
+estrutura de dados que consegue eficiemente atualizar elementos e
+calcular soma dos prefixos em uma tabela de números.
+
+Quando comparado com um _flat array_ de números, a árvore Fenwick
+alcança um balanceamento muito melhor entre duas operações: atualização
+(_update_) do elemento e cálculo da soma do prefíxo. Em uma _flar array_
+de `n` números, você pode tanto armazenar elementos quando a soma dos
+prefixos. Em ambos os casos, computar a soma dos prefixos requer ou 
+atualizar um array de elementos também requerem um tempo linear, contudo,
+a demais operações podem ser realizadas com tempo constante.
+A árvore Fenwick permite ambas as operações serem realizadas com tempo
+`O(log n)`.
+
+Isto é possível devido a representação dos números como uma árvore, aonde
+os valores de cada nó é a soma dos números naquela sub-árvore. A estrutura
+de árvore permite operações a serem realizadas consumindo somente acessos
+a nós em `O(log n)`.
+
+## Implementação de Nós
+
+Árvore Binária Indexada é representada como um _array_. Em cada nó da Árvore
+Binária Indexada armazena a soma de alguns dos elementos de uma _array_
+fornecida. O tamanho da Árvore Binária Indexada é igual a `n` aonde `n` é o
+tamanho do _array_ de entrada. Na presente implementação nós utilizados o
+tamanho `n+1` para uma implementação fácil. Todos os índices são baseados em 1. 
+
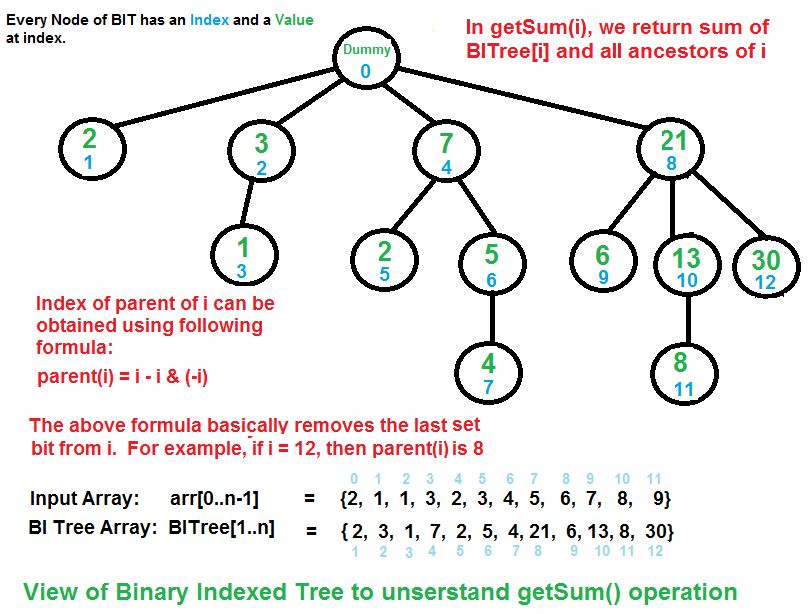
+![Binary Indexed Tree](https://www.geeksforgeeks.org/wp-content/uploads/BITSum.png)
+
+Na imagem abaixo você pode ver o exemplo animado da criação de uma árvore
+binária indexada para o _array_ `[1, 2, 3, 4, 5]`, sendo inseridos um após
+o outro.
+
+![Fenwick Tree](https://upload.wikimedia.org/wikipedia/commons/d/dc/BITDemo.gif)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Fenwick_tree)
+- [GeeksForGeeks](https://www.geeksforgeeks.org/binary-indexed-tree-or-fenwick-tree-2/)
+- [YouTube](https://www.youtube.com/watch?v=CWDQJGaN1gY&index=18&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
--- a/src/data-structures/tree/red-black-tree/README.md
+++ b/src/data-structures/tree/red-black-tree/README.md
@ -1,5 +1,8 @@
 # Red–Black Tree

+_Read this in other languages:_
+[_Português_](README.pt-BR.md) 
+
 A **red–black tree** is a kind of self-balancing binary search 
 tree in computer science. Each node of the binary tree has 
 an extra bit, and that bit is often interpreted as the 
--- a/src/data-structures/tree/red-black-tree/README.pt-BR.md
+++ b/src/data-structures/tree/red-black-tree/README.pt-BR.md
@ -0,0 +1,92 @@
+# Árvore Vermelha-Preta (Red-Black Tree)
+
+Uma **árvore vermelha-preta** é um tipo de árvore de pesquisa
+binária auto balanceada na ciência da computação. Cada nó da 
+árvore binária possui um _bit_ extra, e este _bit_ é frequentemente
+interpretado com a cor (vermelho ou preto) do nó. Estas cores de _bits_
+são utilizadas para garantir que a árvore permanece aproximadamente
+equilibrada durante as operações de inserções e remoções.
+
+O equilíbrio é preservado através da pintura de cada nó da árvore com
+uma das duas cores, de maneira que satisfaça certas propriedades, das
+quais restringe nos piores dos casos, o quão desequilibrada a árvore
+pode se tornar. Quando a árvore é modificada, a nova árvore é
+subsequentemente reorganizada e repintada para restaurar as
+propriedades de coloração. As propriedades são designadas de tal modo que
+esta reorganização e nova pintura podem ser realizadas eficientemente.
+
+O balanceamento de uma árvore não é perfeito, mas é suficientemente bom
+para permitir e garantir uma pesquisa no tempo `O(log n)`, aonde `n` é o
+número total de elementos na árvore.
+Operações de inserções e remoções, juntamente com a reorganização e 
+repintura da árvore, também são executados no tempo `O (log n)`.
+
+Um exemplo de uma árvore vermalha-preta:
+
+![red-black tree](https://upload.wikimedia.org/wikipedia/commons/6/66/Red-black_tree_example.svg)
+
+## Propriedades
+
+Em adição aos requerimentos impostos pela árvore de pesquisa binária,
+as seguintes condições devem ser satisfeitas pela árvore vermelha-preta:
+
+- Cada nó é tanto vermelho ou preto.
+- O nó raíz é preto. Esta regra algumas vezes é omitida.
+Tendo em vista que a raíz pode sempre ser alterada de vermelho para preto,
+mas não de preto para vermelho, esta regra tem pouco efeito na análise.
+- Todas as folhas (Nulo/NIL) são pretas.
+- Caso um nó é vermelho, então seus filhos serão pretos.
+- Cada caminho de um determinado nó para qualquer um dos seus nós nulos (NIL)
+descendentes contém o mesmo número de nós pretos.
+
+Algumas definições: o número de nós pretos da raiz até um nó é a
+**profundidade preta**(_black depth_) do nó; o número uniforme de nós pretos
+em todos os caminhos da raíz até as folhas são chamados de **altura negra**
+(_black-height_) da árvore vermelha-preta.
+
+Essas restrições impõem uma propriedade crítica de árvores vermelhas e pretas:
+_o caminho da raiz até a folha mais distante não possui mais que o dobro do
+comprimento do caminho da raiz até a folha mais próxima_.
+O resultado é que a árvore é grosseiramente balanceada na altura.
+
+Tendo em vista que operações como inserções, remoção e pesquisa de valores
+requerem nos piores dos casos um tempo proporcional a altura da ávore,
+este limite superior teórico na altura permite que as árvores vermelha-preta
+sejam eficientes no pior dos casos, ao contrário das árvores de busca binária
+comuns.
+
+## Balanceamento durante a inserção
+
+### Se o tio é VERMELHO
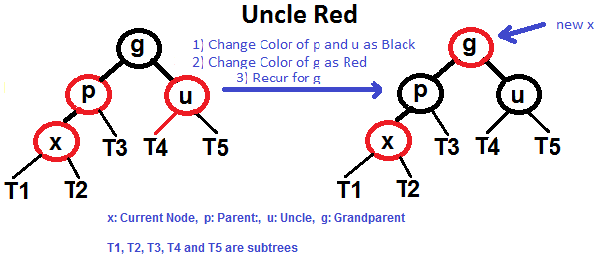
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase2.png)
+
+### Se o tio é PRETO
+
+- Caso Esquerda Esquerda (`p` é o filho a esquerda de `g` e `x`, é o filho a esquerda de `p`)
+- Caso Esquerda Direita (`p` é o filho a esquerda de `g` e `x`, é o filho a direita de `p`)
+- Caso Direita Direita (`p` é o filho a direita de `g` e `x`, é o filho da direita de `p`)
+- Caso Direita Esqueda (`p` é o filho a direita de `g` e `x`, é o filho a esquerda de `p`)
+
+#### Caso Esquerda Esquerda (Veja g, p e x)
+
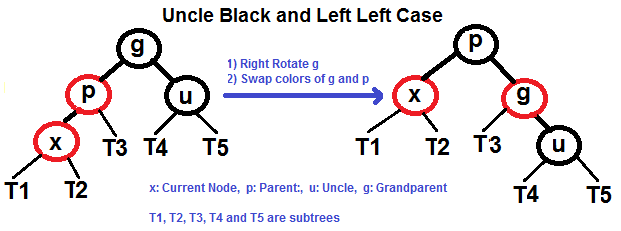
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3a1.png)
+
+#### Caso Esquerda Direita (Veja g, p e x)
+
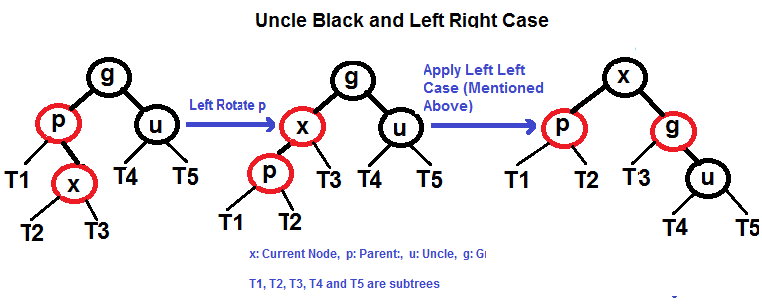
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3b.png)
+
+#### Caso Direita Direita (Veja g, p e x)
+
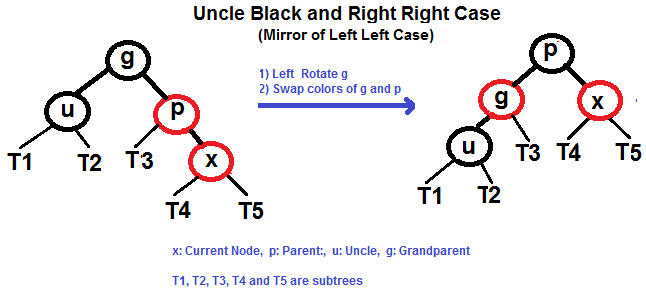
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3c.png)
+
+#### Caso Direita Esquerda (Veja g, p e x)
+
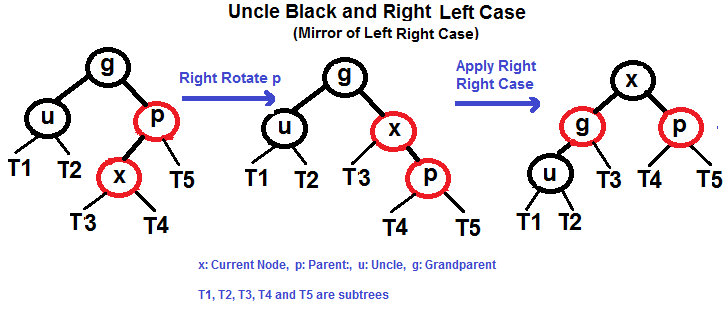
+![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3d.png)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Red%E2%80%93black_tree)
+- [Red Black Tree Insertion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=UaLIHuR1t8Q&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=63)
+- [Red Black Tree Deletion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=CTvfzU_uNKE&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=64)
+- [Red Black Tree Insertion on GeeksForGeeks](https://www.geeksforgeeks.org/red-black-tree-set-2-insert/)
+- [Red Black Tree Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/RedBlack.html)
--- a/src/data-structures/tree/segment-tree/README.md
+++ b/src/data-structures/tree/segment-tree/README.md
@ -1,5 +1,8 @@
 # Segment Tree

+_Read this in other languages:_
+[_Português_](README.pt-BR.md) 
+
 In computer science, a **segment tree** also known as a statistic tree 
 is a tree data structure used for storing information about intervals, 
 or segments. It allows querying which of the stored segments contain 
--- a/src/data-structures/tree/segment-tree/README.pt-BR.md
+++ b/src/data-structures/tree/segment-tree/README.pt-BR.md
@ -0,0 +1,48 @@
+# Árvore de Segmento (Segment Tree)
+
+Na ciência da computação, uma **árvore de segmento** também conhecida como
+árvore estatística é uma árvore de estrutura de dados utilizadas para
+armazenar informações sobre intervalores ou segmentos. Ela permite pesquisas
+no qual os segmentos armazenados contém um ponto fornecido. Isto é,
+em princípio, uma estrutura estática; ou seja, é uma estrutura que não pode
+ser modificada depois de inicializada. Uma estrutura de dados similar é a
+árvore de intervalos.
+
+Uma árvore de segmento é uma árvore binária. A raíz da árvore representa a
+_array_ inteira. Os dois filhos da raíz representam a primeira e a segunda
+metade da _array_. Similarmente, os filhos de cada nó correspondem ao número
+das duas metadas da _array_ correspondente do nó.
+
+Nós construímos a árvore debaixo para cima, com o valor de cada nó sendo o 
+"mínimo" (ou qualquer outra função) dos valores de seus filhos. Isto consumirá
+tempo `O(n log n)`. O número de oprações realizadas é equivalente a altura da
+árvore, pela qual consome tempo `O(log n)`. Para fazer consultas de intervalos,
+cada nó divide a consulta em duas partes, sendo uma sub consulta para cada filho.
+Se uma pesquisa contém todo o _subarray_ de um nó, nós podemos utilizar do valor
+pré-calculado do nó. Utilizando esta otimização, nós podemos provar que somente
+operações mínimas `O(log n)` são realizadas.
+
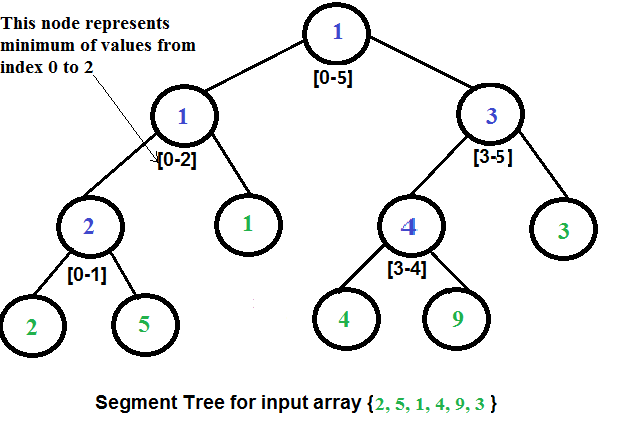
+![Min Segment Tree](https://www.geeksforgeeks.org/wp-content/uploads/RangeMinimumQuery.png)
+
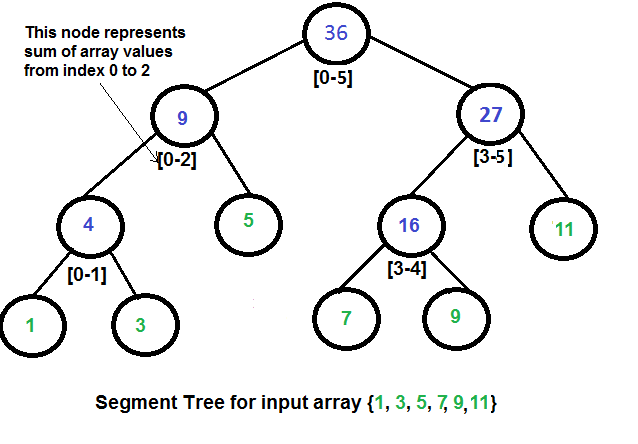
+![Sum Segment Tree](https://www.geeksforgeeks.org/wp-content/uploads/segment-tree1.png)
+
+## Aplicação
+
+Uma árvore de segmento é uma estrutura de dados designada a realizar
+certas operações de _array_ eficientemente, especialmente aquelas envolvendo
+consultas de intervalos.
+
+Aplicações da árvore de segmentos são nas áreas de computação geométrica e
+sistemas de informação geográficos.
+
+A implementação atual da Árvore de Segmentos implica que você pode passar
+qualquer função binária (com dois parâmetros de entradas) e então, você
+será capaz de realizar consultas de intervalos para uma variedade de funções.
+Nos testes você poderá encontrar exemplos realizando `min`, `max` e consultas de
+intervalo `sam` na árvore segmentada (SegmentTree).
+ 
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Segment_tree)
+- [YouTube](https://www.youtube.com/watch?v=ZBHKZF5w4YU&index=65&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+- [GeeksForGeeks](https://www.geeksforgeeks.org/segment-tree-set-1-sum-of-given-range/)
--- a/src/data-structures/trie/README.md
+++ b/src/data-structures/trie/README.md
@ -1,5 +1,10 @@
 # Trie

+_Read this in other languages:_
+[_简体中文_](README.zh-CN.md),
+[_Русский_](README.ru-RU.md),
+[_Português_](README.pt-BR.md)
+
 In computer science, a **trie**, also called digital tree and sometimes 
 radix tree or prefix tree (as they can be searched by prefixes), 
 is a kind of search tree—an ordered tree data structure that is 
--- a/src/data-structures/trie/README.pt-BR.md
+++ b/src/data-structures/trie/README.pt-BR.md
@ -0,0 +1,25 @@
+# Trie
+
+Na ciência da computação, uma **trie**, também chamada de árvore digital (digital tree)
+e algumas vezes de _radix tree_ ou _prefix tree_ (tendo em vista que eles
+podem ser pesquisados por prefixos), é um tipo de árvore de pesquisa, uma
+uma estrutura de dados de árvore ordenada que é usado para armazenar um 
+conjunto dinâmico ou matriz associativa onde as chaves são geralmente _strings_.
+Ao contrário de uma árvore de pesquisa binária (binary search tree),
+nenhum nó na árvore armazena a chave associada a esse nó; em vez disso,
+sua posição na árvore define a chave com a qual ela está associada.
+Todos os descendentes de um nó possuem em comum o prefixo de uma _string_
+associada com aquele nó, e a raiz é associada com uma _string_ vazia.
+Valores não são necessariamente associados a todos nós. Em vez disso,
+os valores tendem a ser associados apenas a folhas e com alguns nós
+internos que correspondem a chaves de interesse.
+
+Para a apresentação otimizada do espaço da árvore de prefixo (_prefix tree_),
+veja árvore de prefixo compacto.
+
+![Trie](https://upload.wikimedia.org/wikipedia/commons/b/be/Trie_example.svg)
+
+## Referências
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Trie)
+- [YouTube](https://www.youtube.com/watch?v=zIjfhVPRZCg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=7&t=0s)
--- a/src/data-structures/trie/README.ru-RU.md
+++ b/src/data-structures/trie/README.ru-RU.md
@ -0,0 +1,26 @@
+# Префиксное дерево
+
+**Префиксное дерево** (также бор, луч, нагруженное или суффиксное дерево) в информатике - упорядоченная древовидная
+структура данных, которая используется для хранения динамических множеств или ассоциативных массивов, где
+ключём обычно выступают строки. Дерево называется префиксным, потому что поиск осуществляется по префиксам.
+
+В отличие от бинарного дерева, узлы не содержат ключи, соответствующие узлу. Представляет собой корневое дерево, каждое
+ребро которого помечено каким-то символом так, что для любого узла все рёбра, соединяющие этот узел с его сыновьями,
+помечены разными символами. Некоторые узлы префиксного дерева выделены (на рисунке они подписаны цифрами) и считается,
+что префиксное дерево содержит данную строку-ключ тогда и только тогда, когда эту строку можно прочитать на пути из
+корня до некоторого выделенного узла.
+
+Таким образом, в отличие от бинарных деревьев поиска, ключ, идентифицирующий конкретный узел дерева, не явно хранится в
+данном узле, а неявно задаётся положением данного узла в дереве. Получить ключ можно выписыванием подряд символов,
+помечающих рёбра на пути от корня до узла. Ключ корня дерева — пустая строка. Часто в выделенных узлах хранят
+дополнительную информацию, связанную с ключом, и обычно выделенными являются только листья и, возможно, некоторые
+внутренние узлы.
+
+![Префиксное дерево](https://upload.wikimedia.org/wikipedia/commons/b/be/Trie_example.svg)
+
+На рисунке представлено префиксное дерево, содержащее ключи «A», «to», «tea», «ted», «ten», «i», «in», «inn».
+
+## Ссылки
+
+- [Wikipedia](https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B5%D1%84%D0%B8%D0%BA%D1%81%D0%BD%D0%BE%D0%B5_%D0%B4%D0%B5%D1%80%D0%B5%D0%B2%D0%BE)
+- [YouTube](https://www.youtube.com/watch?v=zIjfhVPRZCg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=7&t=0s)