Add k-nearest neighbors algorithm.

README.md

@@ -143,7 +143,7 @@ a set of rules that precisely define a sequence of operations.
   * `B` [Caesar Cipher](src/algorithms/cryptography/caesar-cipher) - simple substitution cipher
 * **Machine Learning**
   * `B` [NanoNeuron](https://github.com/trekhleb/nano-neuron) - 7 simple JS functions that illustrate how machines can actually learn (forward/backward propagation)
-  * `B` [KNN](src/algorithms/ML/KNN) - K Nearest Neighbors
+  * `B` [k-NN](src/algorithms/ml/knn) - k-nearest neighbors classification algorithm
 * **Uncategorized**
   * `B` [Tower of Hanoi](src/algorithms/uncategorized/hanoi-tower)
   * `B` [Square Matrix Rotation](src/algorithms/uncategorized/square-matrix-rotation) - in-place algorithm

src/algorithms/ML/KNN/README.md

@@ -1,23 +0,0 @@
-# KNN Algorithm  
-
-KNN stands for K Nearest Neighbors. KNN is a supervised Machine Learning algorithm. It's a classification algorithm, determining the class of a sample vector using a sample data.  
-
-The idea is to calculate the similarity between two data points on the basis of a distance metric. Euclidean distance is used mostly for this task. The algorithm is as follows -  
-
-1. Check for errors like invalid data/labels.
-2. Calculate the euclidean distance of all the data points in training data with the classification point
-3. Sort the distances of points along with their classes in ascending order
-4. Take the initial "K" classes and find the mode to get the most similar class
-5. Report the most similar class  
-
-Here is a visualization for better understanding -  
-
-![KNN Visualization](https://media.geeksforgeeks.org/wp-content/uploads/graph2-2.png)  
-
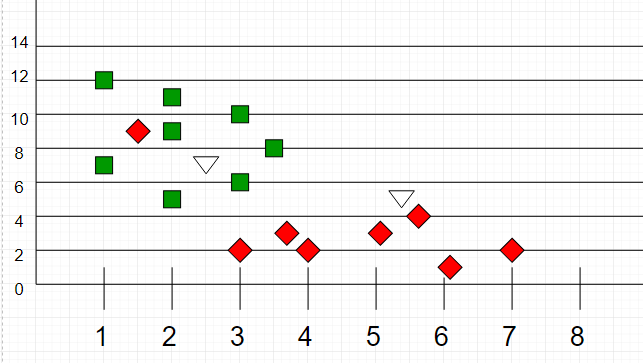
-Here, as we can see, the classification of unknown points will be judged by their proximity to other points.
-
-It is important to note that "K" is preferred to have odd values in order to break ties. Usually "K" is taken as 3 or 5.  
-
-## References
-
-- [GeeksforGeeks](https://media.geeksforgeeks.org/wp-content/uploads/graph2-2.png)

src/algorithms/ML/KNN/__test__/knn.test.js

@@ -1,42 +0,0 @@
-import KNN from '../knn';
-
-describe('KNN', () => {
-  test('should throw an error on invalid data', () => {
-    expect(() => {
-      KNN();
-    }).toThrowError();
-  });
-  test('should throw an error on invalid labels', () => {
-    const nolabels = () => {
-      KNN([[1, 1]]);
-    };
-    expect(nolabels).toThrowError();
-  });
-  it('should throw an error on not giving classification vector', () => {
-    const noclassification = () => {
-      KNN([[1, 1]], [1]);
-    };
-    expect(noclassification).toThrowError();
-  });
-  it('should throw an error on not giving classification vector', () => {
-    const inconsistent = () => {
-      KNN([[1, 1]], [1], [1]);
-    };
-    expect(inconsistent).toThrowError();
-  });
-  it('should find the nearest neighbour', () => {
-    let dataX = [[1, 1], [2, 2]];
-    let dataY = [1, 2];
-    expect(KNN(dataX, dataY, [1, 1])).toBe(1);
-
-    dataX = [[1, 1], [6, 2], [3, 3], [4, 5], [9, 2], [2, 4], [8, 7]];
-    dataY = [1, 2, 1, 2, 1, 2, 1];
-    expect(KNN(dataX, dataY, [1.25, 1.25]))
-      .toBe(1);
-
-    dataX = [[1, 1], [6, 2], [3, 3], [4, 5], [9, 2], [2, 4], [8, 7]];
-    dataY = [1, 2, 1, 2, 1, 2, 1];
-    expect(KNN(dataX, dataY, [1.25, 1.25], 5))
-      .toBe(2);
-  });
-});

src/algorithms/ML/KNN/knn.js

@@ -1,60 +0,0 @@
-/**
- * @param {object} dataY
- * @param {object} dataX
- * @param {object} toClassify
- * @param {number} k
- * @return {number}
- */
-export default function KNN(dataX, dataY, toClassify, K) {
-  let k = -1;
-
-  if (K === undefined) {
-    k = 3;
-  } else {
-    k = K;
-  }
-
-  // creating function to calculate the euclidean distance between 2 vectors
-  function euclideanDistance(x1, x2) {
-    // checking errors
-    if (x1.length !== x2.length) {
-      throw new Error('inconsistency between data and classification vector.');
-    }
-    // calculate the euclidean distance between 2 vectors and return
-    let totalSSE = 0;
-    for (let j = 0; j < x1.length; j += 1) {
-      totalSSE += (x1[j] - x2[j]) ** 2;
-    }
-    return Number(Math.sqrt(totalSSE).toFixed(2));
-  }
-
-  // starting algorithm
-
-  // calculate distance from toClassify to each point for all dimensions in dataX
-  // store distance and point's class_index into distance_class_list
-  let distanceList = [];
-  for (let i = 0; i < dataX.length; i += 1) {
-    const tmStore = [];
-    tmStore.push(euclideanDistance(dataX[i], toClassify));
-    tmStore.push(dataY[i]);
-    distanceList[i] = tmStore;
-  }
-
-  // sort distanceList
-  // take initial k values, count with class index
-  distanceList = distanceList.sort().slice(0, k);
-
-  // count the number of instances of each class in top k members
-  // with that maintain record of highest count class simultanously
-  const modeK = {};
-  const maxm = [-1, -1];
-  for (let i = 0; i < Math.min(k, distanceList.length); i += 1) {
-    if (distanceList[i][1] in modeK) modeK[distanceList[i][1]] += 1;
-    else modeK[distanceList[i][1]] = 1;
-    if (modeK[distanceList[i][1]] > maxm[0]) {
-      [maxm[0], maxm[1]] = [modeK[distanceList[i][1]], distanceList[i][1]];
-    }
-  }
-  // return the class with highest count from maxm
-  return maxm[1];
-}

src/algorithms/ml/knn/README.md

@@ -0,0 +1,41 @@
+# k-Nearest Neighbors Algorithm
+
+The **k-nearest neighbors algorithm (k-NN)** is a supervised Machine Learning algorithm. It's a classification algorithm, determining the class of a sample vector using a sample data.
+
+In k-NN classification, the output is a class membership. An object is classified by a plurality vote of its neighbors, with the object being assigned to the class most common among its `k` nearest neighbors (`k` is a positive integer, typically small). If `k = 1`, then the object is simply assigned to the class of that single nearest neighbor.
+
+The idea is to calculate the similarity between two data points on the basis of a distance metric. [Euclidean distance](https://en.wikipedia.org/wiki/Euclidean_distance) is used mostly for this task.
+
+![Euclidean distance between two points](https://upload.wikimedia.org/wikipedia/commons/5/55/Euclidean_distance_2d.svg)
+
+_Image source: [Wikipedia](https://en.wikipedia.org/wiki/Euclidean_distance)_
+
+The algorithm is as follows:
+
+1. Check for errors like invalid data/labels.
+2. Calculate the euclidean distance of all the data points in training data with the classification point
+3. Sort the distances of points along with their classes in ascending order
+4. Take the initial `K` classes and find the mode to get the most similar class
+5. Report the most similar class
+
+Here is a visualization of k-NN classification for better understanding:
+
+![KNN Visualization 1](https://upload.wikimedia.org/wikipedia/commons/e/e7/KnnClassification.svg)
+
+_Image source: [Wikipedia](https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm)_
+
+The test sample (green dot) should be classified either to blue squares or to red triangles. If `k = 3` (solid line circle) it is assigned to the red triangles because there are `2` triangles and only `1` square inside the inner circle. If `k = 5` (dashed line circle) it is assigned to the blue squares (`3` squares vs. `2` triangles inside the outer circle).
+
+Another k-NN classification example:
+
+![KNN Visualization 2](https://media.geeksforgeeks.org/wp-content/uploads/graph2-2.png)
+
+_Image source: [GeeksForGeeks](https://media.geeksforgeeks.org/wp-content/uploads/graph2-2.png)_
+
+Here, as we can see, the classification of unknown points will be judged by their proximity to other points.
+
+It is important to note that `K` is preferred to have odd values in order to break ties. Usually `K` is taken as `3` or `5`.
+
+## References
+
+- [k-nearest neighbors algorithm on Wikipedia](https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm)

src/algorithms/ml/knn/__test__/knn.test.js

@@ -0,0 +1,71 @@
+import kNN from '../kNN';
+
+describe('kNN', () => {
+  it('should throw an error on invalid data', () => {
+    expect(() => {
+      kNN();
+    }).toThrowError('Either dataSet or labels or toClassify were not set');
+  });
+
+  it('should throw an error on invalid labels', () => {
+    const noLabels = () => {
+      kNN([[1, 1]]);
+    };
+    expect(noLabels).toThrowError('Either dataSet or labels or toClassify were not set');
+  });
+
+  it('should throw an error on not giving classification vector', () => {
+    const noClassification = () => {
+      kNN([[1, 1]], [1]);
+    };
+    expect(noClassification).toThrowError('Either dataSet or labels or toClassify were not set');
+  });
+
+  it('should throw an error on not giving classification vector', () => {
+    const inconsistent = () => {
+      kNN([[1, 1]], [1], [1]);
+    };
+    expect(inconsistent).toThrowError('Inconsistent vector lengths');
+  });
+
+  it('should find the nearest neighbour', () => {
+    let dataSet;
+    let labels;
+    let toClassify;
+    let expectedClass;
+
+    dataSet = [[1, 1], [2, 2]];
+    labels = [1, 2];
+    toClassify = [1, 1];
+    expectedClass = 1;
+    expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass);
+
+    dataSet = [[1, 1], [6, 2], [3, 3], [4, 5], [9, 2], [2, 4], [8, 7]];
+    labels = [1, 2, 1, 2, 1, 2, 1];
+    toClassify = [1.25, 1.25];
+    expectedClass = 1;
+    expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass);
+
+    dataSet = [[1, 1], [6, 2], [3, 3], [4, 5], [9, 2], [2, 4], [8, 7]];
+    labels = [1, 2, 1, 2, 1, 2, 1];
+    toClassify = [1.25, 1.25];
+    expectedClass = 2;
+    expect(kNN(dataSet, labels, toClassify, 5)).toBe(expectedClass);
+  });
+
+  it('should find the nearest neighbour with equal distances', () => {
+    const dataSet = [[0, 0], [1, 1], [0, 2]];
+    const labels = [1, 3, 3];
+    const toClassify = [0, 1];
+    const expectedClass = 3;
+    expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass);
+  });
+
+  it('should find the nearest neighbour in 3D space', () => {
+    const dataSet = [[0, 0, 0], [0, 1, 1], [0, 0, 2]];
+    const labels = [1, 3, 3];
+    const toClassify = [0, 0, 1];
+    const expectedClass = 3;
+    expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass);
+  });
+});

src/algorithms/ml/knn/kNN.js

@@ -0,0 +1,77 @@
+/**
+ * Calculates calculate the euclidean distance between 2 vectors.
+ *
+ * @param {number[]} x1
+ * @param {number[]} x2
+ * @returns {number}
+ */
+function euclideanDistance(x1, x2) {
+  // Checking for errors.
+  if (x1.length !== x2.length) {
+    throw new Error('Inconsistent vector lengths');
+  }
+  // Calculate the euclidean distance between 2 vectors and return.
+  let squaresTotal = 0;
+  for (let i = 0; i < x1.length; i += 1) {
+    squaresTotal += (x1[i] - x2[i]) ** 2;
+  }
+  return Number(Math.sqrt(squaresTotal).toFixed(2));
+}
+
+/**
+ * Classifies the point in space based on k-nearest neighbors algorithm.
+ *
+ * @param {number[][]} dataSet - array of data points, i.e. [[0, 1], [3, 4], [5, 7]]
+ * @param {number[]} labels - array of classes (labels), i.e. [1, 1, 2]
+ * @param {number[]} toClassify - the point in space that needs to be classified, i.e. [5, 4]
+ * @param {number} k - number of nearest neighbors which will be taken into account (preferably odd)
+ * @return {number} - the class of the point
+ */
+export default function kNN(
+  dataSet,
+  labels,
+  toClassify,
+  k = 3,
+) {
+  if (!dataSet || !labels || !toClassify) {
+    throw new Error('Either dataSet or labels or toClassify were not set');
+  }
+
+  // Calculate distance from toClassify to each point for all dimensions in dataSet.
+  // Store distance and point's label into distances list.
+  const distances = [];
+  for (let i = 0; i < dataSet.length; i += 1) {
+    distances.push({
+      dist: euclideanDistance(dataSet[i], toClassify),
+      label: labels[i],
+    });
+  }
+
+  // Sort distances list (from closer point to further ones).
+  // Take initial k values, count with class index
+  const kNearest = distances.sort((a, b) => {
+    if (a.dist === b.dist) {
+      return 0;
+    }
+    return a.dist < b.dist ? -1 : 1;
+  }).slice(0, k);
+
+  // Count the number of instances of each class in top k members.
+  const labelsCounter = {};
+  let topClass = 0;
+  let topClassCount = 0;
+  for (let i = 0; i < kNearest.length; i += 1) {
+    if (kNearest[i].label in labelsCounter) {
+      labelsCounter[kNearest[i].label] += 1;
+    } else {
+      labelsCounter[kNearest[i].label] = 1;
+    }
+    if (labelsCounter[kNearest[i].label] > topClassCount) {
+      topClassCount = labelsCounter[kNearest[i].label];
+      topClass = kNearest[i].label;
+    }
+  }
+
+  // Return the class with highest count.
+  return topClass;
+}