mirror of
https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git
synced 2024-11-10 11:09:43 +08:00
Add Knight's tour.
This commit is contained in:
parent
d2c6d14acd
commit
476c0acb4a
@ -80,6 +80,7 @@
|
||||
* **Uncategorized**
|
||||
* [Tower of Hanoi](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/uncategorized/hanoi-tower)
|
||||
* [N-Queens Problem](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/uncategorized/n-queens)
|
||||
* [Knight's Tour](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/uncategorized/knight-tour)
|
||||
* Union-Find
|
||||
* Maze
|
||||
* Sudoku
|
||||
@ -114,6 +115,7 @@
|
||||
* **Backtracking**
|
||||
* [Hamiltonian Cycle](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/hamiltonian-cycle) - Visit every vertex exactly once
|
||||
* [N-Queens Problem](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/uncategorized/n-queens)
|
||||
* [Knight's Tour](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/uncategorized/knight-tour)
|
||||
* **Branch & Bound**
|
||||
|
||||
## How to use this repository
|
||||
|
||||
33
src/algorithms/uncategorized/knight-tour/README.md
Normal file
33
src/algorithms/uncategorized/knight-tour/README.md
Normal file
@ -0,0 +1,33 @@
|
||||
# Knight's Tour
|
||||
|
||||
A **knight's tour** is a sequence of moves of a knight on a chessboard
|
||||
such that the knight visits every square only once. If the knight
|
||||
ends on a square that is one knight's move from the beginning
|
||||
square (so that it could tour the board again immediately,
|
||||
following the same path), the tour is **closed**, otherwise it
|
||||
is **open**.
|
||||
|
||||
The **knight's tour problem** is the mathematical problem of
|
||||
finding a knight's tour. Creating a program to find a knight's
|
||||
tour is a common problem given to computer science students.
|
||||
Variations of the knight's tour problem involve chessboards of
|
||||
different sizes than the usual `8×8`, as well as irregular
|
||||
(non-rectangular) boards.
|
||||
|
||||
The knight's tour problem is an instance of the more
|
||||
general **Hamiltonian path problem** in graph theory. The problem of finding
|
||||
a closed knight's tour is similarly an instance of the Hamiltonian
|
||||
cycle problem.
|
||||
|
||||
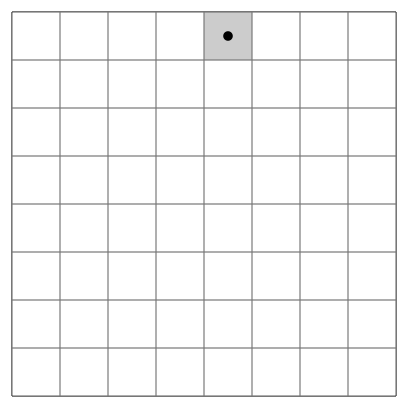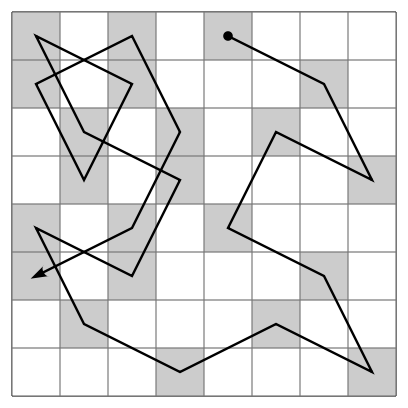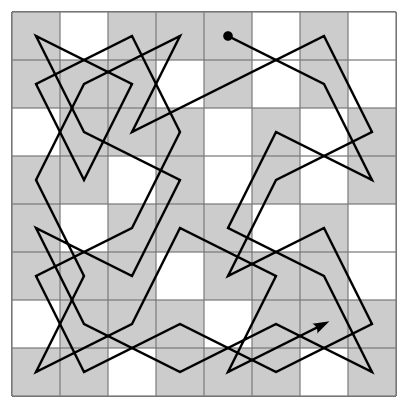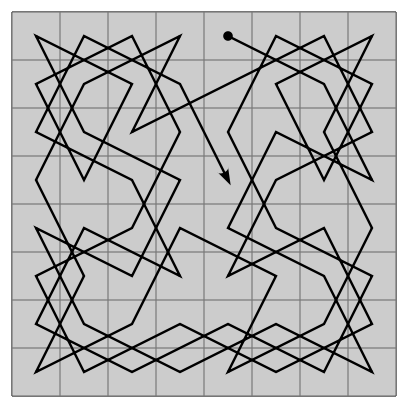
|
||||
|
||||
An open knight's tour of a chessboard.
|
||||
|
||||

|
||||
|
||||
An animation of an open knight's tour on a 5 by 5 board.
|
||||
|
||||
## References
|
||||
|
||||
- [Wikipedia](https://en.wikipedia.org/wiki/Knight%27s_tour)
|
||||
- [GeeksForGeeks](https://www.geeksforgeeks.org/backtracking-set-1-the-knights-tour-problem/)
|
||||
@ -0,0 +1,43 @@
|
||||
import knightTour from '../knightTour';
|
||||
|
||||
describe('knightTour', () => {
|
||||
it('should not find solution on 3x3 board', () => {
|
||||
const moves = knightTour(3);
|
||||
|
||||
expect(moves.length).toBe(0);
|
||||
});
|
||||
|
||||
it('should find one solution to do knight tour on 5x5 board', () => {
|
||||
const moves = knightTour(5);
|
||||
|
||||
expect(moves.length).toBe(25);
|
||||
|
||||
expect(moves).toEqual([
|
||||
[0, 0],
|
||||
[1, 2],
|
||||
[2, 0],
|
||||
[0, 1],
|
||||
[1, 3],
|
||||
[3, 4],
|
||||
[2, 2],
|
||||
[4, 1],
|
||||
[3, 3],
|
||||
[1, 4],
|
||||
[0, 2],
|
||||
[1, 0],
|
||||
[3, 1],
|
||||
[4, 3],
|
||||
[2, 4],
|
||||
[0, 3],
|
||||
[1, 1],
|
||||
[3, 0],
|
||||
[4, 2],
|
||||
[2, 1],
|
||||
[4, 0],
|
||||
[3, 2],
|
||||
[4, 4],
|
||||
[2, 3],
|
||||
[0, 4],
|
||||
]);
|
||||
});
|
||||
});
|
||||
112
src/algorithms/uncategorized/knight-tour/knightTour.js
Normal file
112
src/algorithms/uncategorized/knight-tour/knightTour.js
Normal file
@ -0,0 +1,112 @@
|
||||
/**
|
||||
* @param {number[][]} chessboard
|
||||
* @param {number[]} position
|
||||
* @return {number[][]}
|
||||
*/
|
||||
function getPossibleMoves(chessboard, position) {
|
||||
// Generate all knight moves (event those that goes beyond the board).
|
||||
const possibleMoves = [
|
||||
[position[0] - 1, position[1] - 2],
|
||||
[position[0] - 2, position[1] - 1],
|
||||
[position[0] + 1, position[1] - 2],
|
||||
[position[0] + 2, position[1] - 1],
|
||||
[position[0] - 2, position[1] + 1],
|
||||
[position[0] - 1, position[1] + 2],
|
||||
[position[0] + 1, position[1] + 2],
|
||||
[position[0] + 2, position[1] + 1],
|
||||
];
|
||||
|
||||
// Filter out all moves that go beyond the board.
|
||||
return possibleMoves.filter((move) => {
|
||||
const boardSize = chessboard.length;
|
||||
return move[0] >= 0 && move[1] >= 0 && move[0] < boardSize && move[1] < boardSize;
|
||||
});
|
||||
}
|
||||
|
||||
/**
|
||||
* @param {number[][]} chessboard
|
||||
* @param {number[]} move
|
||||
* @return {boolean}
|
||||
*/
|
||||
function isMoveAllowed(chessboard, move) {
|
||||
return chessboard[move[0]][move[1]] !== 1;
|
||||
}
|
||||
|
||||
/**
|
||||
* @param {number[][]} chessboard
|
||||
* @param {number[][]} moves
|
||||
* @return {boolean}
|
||||
*/
|
||||
function isBoardCompletelyVisited(chessboard, moves) {
|
||||
const totalPossibleMovesCount = chessboard.length ** 2;
|
||||
const existingMovesCount = moves.length;
|
||||
|
||||
return totalPossibleMovesCount === existingMovesCount;
|
||||
}
|
||||
|
||||
/**
|
||||
* @param {number[][]} chessboard
|
||||
* @param {number[][]} moves
|
||||
* @return {boolean}
|
||||
*/
|
||||
function knightTourRecursive(chessboard, moves) {
|
||||
const currentChessboard = chessboard;
|
||||
|
||||
// If board has been completely visited then we've found a solution.
|
||||
if (isBoardCompletelyVisited(currentChessboard, moves)) {
|
||||
return true;
|
||||
}
|
||||
|
||||
// Get next possible knight moves.
|
||||
const lastMove = moves[moves.length - 1];
|
||||
const possibleMoves = getPossibleMoves(currentChessboard, lastMove);
|
||||
|
||||
// Try to do next possible moves.
|
||||
for (let moveIndex = 0; moveIndex < possibleMoves.length; moveIndex += 1) {
|
||||
const currentMove = possibleMoves[moveIndex];
|
||||
|
||||
// Check if current move is allowed. We aren't allowed to go to
|
||||
// the same cells twice.
|
||||
if (isMoveAllowed(currentChessboard, currentMove)) {
|
||||
// Actually do the move.
|
||||
moves.push(currentMove);
|
||||
currentChessboard[currentMove[0]][currentMove[1]] = 1;
|
||||
|
||||
// If further moves starting from current are successful then
|
||||
// return true meaning the solution is found.
|
||||
if (knightTourRecursive(currentChessboard, moves)) {
|
||||
return true;
|
||||
}
|
||||
|
||||
// BACKTRACKING.
|
||||
// If current move was unsuccessful then step back and try to do another move.
|
||||
moves.pop();
|
||||
currentChessboard[currentMove[0]][currentMove[1]] = 0;
|
||||
}
|
||||
}
|
||||
|
||||
// Return false if we haven't found solution.
|
||||
return false;
|
||||
}
|
||||
|
||||
/**
|
||||
* @param {number} chessboardSize
|
||||
* @return {number[][]}
|
||||
*/
|
||||
export default function knightTour(chessboardSize) {
|
||||
// Init chessboard.
|
||||
const chessboard = Array(chessboardSize).fill(null).map(() => Array(chessboardSize).fill(0));
|
||||
|
||||
// Init moves array.
|
||||
const moves = [];
|
||||
|
||||
// Do first move and place the knight to the 0x0 cell.
|
||||
const firstMove = [0, 0];
|
||||
moves.push(firstMove);
|
||||
chessboard[firstMove[0]][firstMove[0]] = 1;
|
||||
|
||||
// Recursively try to do the next move.
|
||||
const solutionWasFound = knightTourRecursive(chessboard, moves);
|
||||
|
||||
return solutionWasFound ? moves : [];
|
||||
}
|
||||
Loading…
Reference in New Issue
Block a user