mirror of
https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git
synced 2024-12-26 23:21:18 +08:00
Add detect cycle.
This commit is contained in:
parent
843893e8e7
commit
47ac5fcd70
@ -68,7 +68,7 @@
|
|||||||
* [Breadth-First Search](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/breadth-first-search) (BFS)
|
* [Breadth-First Search](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/breadth-first-search) (BFS)
|
||||||
* [Dijkstra Algorithm](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/dijkstra) - finding shortest path to all graph vertices
|
* [Dijkstra Algorithm](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/dijkstra) - finding shortest path to all graph vertices
|
||||||
* [Bellman-Ford Algorithm](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/bellman-ford) - finding shortest path to all graph vertices
|
* [Bellman-Ford Algorithm](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/bellman-ford) - finding shortest path to all graph vertices
|
||||||
* Detect Cycle
|
* [Detect Cycle](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/detect-cycle)
|
||||||
* Topological Sorting
|
* Topological Sorting
|
||||||
* Eulerian path, Eulerian circuit
|
* Eulerian path, Eulerian circuit
|
||||||
* Strongly Connected Component algorithm
|
* Strongly Connected Component algorithm
|
||||||
|
|||||||
60
src/algorithms/graph/detect-cycle/README.md
Normal file
60
src/algorithms/graph/detect-cycle/README.md
Normal file
@ -0,0 +1,60 @@
|
|||||||
|
# Detect Cycle in Graphs
|
||||||
|
|
||||||
|
In graph theory, a **cycle** is a path of edges and vertices
|
||||||
|
wherein a vertex is reachable from itself. There are several
|
||||||
|
different types of cycles, principally a **closed walk** and
|
||||||
|
a **simple cycle**.
|
||||||
|
|
||||||
|
## Definitions
|
||||||
|
|
||||||
|
A **closed walk** consists of a sequence of vertices starting
|
||||||
|
and ending at the same vertex, with each two consecutive vertices
|
||||||
|
in the sequence adjacent to each other in the graph. In a directed graph,
|
||||||
|
each edge must be traversed by the walk consistently with its direction:
|
||||||
|
the edge must be oriented from the earlier of two consecutive vertices
|
||||||
|
to the later of the two vertices in the sequence.
|
||||||
|
The choice of starting vertex is not important: traversing the same cyclic
|
||||||
|
sequence of edges from different starting vertices produces the same closed walk.
|
||||||
|
|
||||||
|
A **simple cycle may** be defined either as a closed walk with no repetitions of
|
||||||
|
vertices and edges allowed, other than the repetition of the starting and ending
|
||||||
|
vertex, or as the set of edges in such a walk. The two definitions are equivalent
|
||||||
|
in directed graphs, where simple cycles are also called directed cycles: the cyclic
|
||||||
|
sequence of vertices and edges in a walk is completely determined by the set of
|
||||||
|
edges that it uses. In undirected graphs the set of edges of a cycle can be
|
||||||
|
traversed by a walk in either of two directions, giving two possible directed cycles
|
||||||
|
for every undirected cycle. A circuit can be a closed walk allowing repetitions of
|
||||||
|
vertices but not edges; however, it can also be a simple cycle, so explicit
|
||||||
|
definition is recommended when it is used.
|
||||||
|
|
||||||
|
## Example
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
A graph with edges colored to illustrate **path** `H-A-B` (green), closed path or
|
||||||
|
**walk with a repeated vertex** `B-D-E-F-D-C-B` (blue) and a **cycle with no repeated edge** or
|
||||||
|
vertex `H-D-G-H` (red)
|
||||||
|
|
||||||
|
### Cycle in undirected graph
|
||||||
|
|
||||||
|
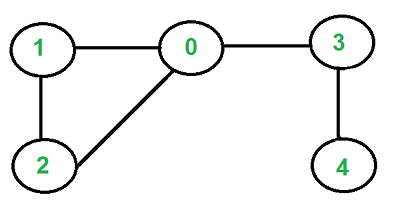
|
||||||
|
|
||||||
|
### Cycle in directed graph
|
||||||
|
|
||||||
|
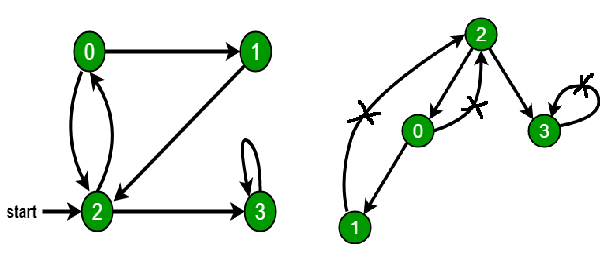
|
||||||
|
|
||||||
|
## References
|
||||||
|
|
||||||
|
General information:
|
||||||
|
|
||||||
|
- [Wikipedia](https://en.wikipedia.org/wiki/Cycle_(graph_theory))
|
||||||
|
|
||||||
|
Cycles in undirected graphs:
|
||||||
|
|
||||||
|
- [Detect Cycle in Undirected Graph on GeeksForGeeks](https://www.geeksforgeeks.org/detect-cycle-undirected-graph/)
|
||||||
|
- [Detect Cycle in Undirected Graph Algorithm on YouTube](https://www.youtube.com/watch?v=n_t0a_8H8VY)
|
||||||
|
|
||||||
|
Cycles in directed graphs:
|
||||||
|
|
||||||
|
- [Detect Cycle in Directed Graph on GeeksForGeeks](https://www.geeksforgeeks.org/detect-cycle-in-a-graph/)
|
||||||
|
- [Detect Cycle in Directed Graph Algorithm on YouTube](https://www.youtube.com/watch?v=rKQaZuoUR4M)
|
||||||
@ -0,0 +1,36 @@
|
|||||||
|
import GraphVertex from '../../../../data-structures/graph/GraphVertex';
|
||||||
|
import GraphEdge from '../../../../data-structures/graph/GraphEdge';
|
||||||
|
import Graph from '../../../../data-structures/graph/Graph';
|
||||||
|
import detectUndirectedCycle from '../detectUndirectedCycle';
|
||||||
|
|
||||||
|
describe('detectUndirectedCycle', () => {
|
||||||
|
it('should detect undirected cycle', () => {
|
||||||
|
const vertexA = new GraphVertex('A');
|
||||||
|
const vertexB = new GraphVertex('B');
|
||||||
|
const vertexC = new GraphVertex('C');
|
||||||
|
const vertexD = new GraphVertex('D');
|
||||||
|
const vertexE = new GraphVertex('E');
|
||||||
|
const vertexF = new GraphVertex('F');
|
||||||
|
|
||||||
|
const edgeAF = new GraphEdge(vertexA, vertexF);
|
||||||
|
const edgeAB = new GraphEdge(vertexA, vertexB);
|
||||||
|
const edgeBE = new GraphEdge(vertexB, vertexE);
|
||||||
|
const edgeBC = new GraphEdge(vertexB, vertexC);
|
||||||
|
const edgeCD = new GraphEdge(vertexC, vertexD);
|
||||||
|
const edgeDE = new GraphEdge(vertexD, vertexE);
|
||||||
|
|
||||||
|
const graph = new Graph();
|
||||||
|
graph
|
||||||
|
.addEdge(edgeAF)
|
||||||
|
.addEdge(edgeAB)
|
||||||
|
.addEdge(edgeBE)
|
||||||
|
.addEdge(edgeBC)
|
||||||
|
.addEdge(edgeCD);
|
||||||
|
|
||||||
|
expect(detectUndirectedCycle(graph)).toBeFalsy();
|
||||||
|
|
||||||
|
graph.addEdge(edgeDE);
|
||||||
|
|
||||||
|
expect(detectUndirectedCycle(graph)).toBeTruthy();
|
||||||
|
});
|
||||||
|
});
|
||||||
32
src/algorithms/graph/detect-cycle/detectUndirectedCycle.js
Normal file
32
src/algorithms/graph/detect-cycle/detectUndirectedCycle.js
Normal file
@ -0,0 +1,32 @@
|
|||||||
|
import DisjointSet from '../../../data-structures/disjoint-set/DisjointSet';
|
||||||
|
|
||||||
|
/**
|
||||||
|
* Detect cycle in undirected graph using disjoint sets.
|
||||||
|
*
|
||||||
|
* @param {Graph} graph
|
||||||
|
*/
|
||||||
|
|
||||||
|
export default function detectUndirectedCycle(graph) {
|
||||||
|
// Create initial singleton disjoint sets for each graph vertex.
|
||||||
|
/** @param {GraphVertex} graphVertex */
|
||||||
|
const keyExtractor = graphVertex => graphVertex.getKey();
|
||||||
|
const disjointSet = new DisjointSet(keyExtractor);
|
||||||
|
graph.getAllVertices().forEach(graphVertex => disjointSet.makeSet(graphVertex));
|
||||||
|
|
||||||
|
// Go trough all graph edges one by one and check if edge vertices are from the
|
||||||
|
// different sets. In this case joint those sets together. Do this until you find
|
||||||
|
// an edge where to edge vertices are already in one set. This means that current
|
||||||
|
// edge will create a cycle.
|
||||||
|
let cycleFound = false;
|
||||||
|
/** @param {GraphEdge} graphEdge */
|
||||||
|
graph.getAllEdges().forEach((graphEdge) => {
|
||||||
|
if (disjointSet.inSameSet(graphEdge.startVertex, graphEdge.endVertex)) {
|
||||||
|
// Cycle found.
|
||||||
|
cycleFound = true;
|
||||||
|
} else {
|
||||||
|
disjointSet.union(graphEdge.startVertex, graphEdge.endVertex);
|
||||||
|
}
|
||||||
|
});
|
||||||
|
|
||||||
|
return cycleFound;
|
||||||
|
}
|
||||||
@ -4,6 +4,7 @@ export default class Graph {
|
|||||||
*/
|
*/
|
||||||
constructor(isDirected = false) {
|
constructor(isDirected = false) {
|
||||||
this.vertices = {};
|
this.vertices = {};
|
||||||
|
this.edges = {};
|
||||||
this.isDirected = isDirected;
|
this.isDirected = isDirected;
|
||||||
}
|
}
|
||||||
|
|
||||||
@ -39,6 +40,13 @@ export default class Graph {
|
|||||||
return Object.values(this.vertices);
|
return Object.values(this.vertices);
|
||||||
}
|
}
|
||||||
|
|
||||||
|
/**
|
||||||
|
* @return {GraphEdge[]}
|
||||||
|
*/
|
||||||
|
getAllEdges() {
|
||||||
|
return Object.values(this.edges);
|
||||||
|
}
|
||||||
|
|
||||||
/**
|
/**
|
||||||
* @param {GraphEdge} edge
|
* @param {GraphEdge} edge
|
||||||
* @returns {Graph}
|
* @returns {Graph}
|
||||||
@ -60,7 +68,12 @@ export default class Graph {
|
|||||||
endVertex = this.getVertexByKey(edge.endVertex.getKey());
|
endVertex = this.getVertexByKey(edge.endVertex.getKey());
|
||||||
}
|
}
|
||||||
|
|
||||||
// @TODO: Check if edge has been already added.
|
// Check if edge has been already added.
|
||||||
|
if (this.edges[edge.getKey()]) {
|
||||||
|
throw new Error('Edge has already been added before');
|
||||||
|
} else {
|
||||||
|
this.edges[edge.getKey()] = edge;
|
||||||
|
}
|
||||||
|
|
||||||
// Add edge to the vertices.
|
// Add edge to the vertices.
|
||||||
if (this.isDirected) {
|
if (this.isDirected) {
|
||||||
|
|||||||
@ -9,4 +9,14 @@ export default class GraphEdge {
|
|||||||
this.endVertex = endVertex;
|
this.endVertex = endVertex;
|
||||||
this.weight = weight;
|
this.weight = weight;
|
||||||
}
|
}
|
||||||
|
|
||||||
|
/**
|
||||||
|
* @return {string}
|
||||||
|
*/
|
||||||
|
getKey() {
|
||||||
|
const startVertexKey = this.startVertex.getKey();
|
||||||
|
const endVertexKey = this.endVertex.getKey();
|
||||||
|
|
||||||
|
return `${startVertexKey}_${endVertexKey}`;
|
||||||
|
}
|
||||||
}
|
}
|
||||||
|
|||||||
@ -136,4 +136,42 @@ describe('Graph', () => {
|
|||||||
expect(neighbors[0]).toEqual(vertexB);
|
expect(neighbors[0]).toEqual(vertexB);
|
||||||
expect(neighbors[1]).toEqual(vertexC);
|
expect(neighbors[1]).toEqual(vertexC);
|
||||||
});
|
});
|
||||||
|
|
||||||
|
it('should throw an error when trying to add edge twice', () => {
|
||||||
|
function addSameEdgeTwice() {
|
||||||
|
const graph = new Graph(true);
|
||||||
|
|
||||||
|
const vertexA = new GraphVertex('A');
|
||||||
|
const vertexB = new GraphVertex('B');
|
||||||
|
|
||||||
|
const edgeAB = new GraphEdge(vertexA, vertexB);
|
||||||
|
|
||||||
|
graph
|
||||||
|
.addEdge(edgeAB)
|
||||||
|
.addEdge(edgeAB);
|
||||||
|
}
|
||||||
|
|
||||||
|
expect(addSameEdgeTwice).toThrow();
|
||||||
|
});
|
||||||
|
|
||||||
|
it('should return the list of all added edges', () => {
|
||||||
|
const graph = new Graph(true);
|
||||||
|
|
||||||
|
const vertexA = new GraphVertex('A');
|
||||||
|
const vertexB = new GraphVertex('B');
|
||||||
|
const vertexC = new GraphVertex('C');
|
||||||
|
|
||||||
|
const edgeAB = new GraphEdge(vertexA, vertexB);
|
||||||
|
const edgeBC = new GraphEdge(vertexB, vertexC);
|
||||||
|
|
||||||
|
graph
|
||||||
|
.addEdge(edgeAB)
|
||||||
|
.addEdge(edgeBC);
|
||||||
|
|
||||||
|
const edges = graph.getAllEdges();
|
||||||
|
|
||||||
|
expect(edges.length).toBe(2);
|
||||||
|
expect(edges[0]).toEqual(edgeAB);
|
||||||
|
expect(edges[1]).toEqual(edgeBC);
|
||||||
|
});
|
||||||
});
|
});
|
||||||
|
|||||||
@ -7,6 +7,7 @@ describe('GraphEdge', () => {
|
|||||||
const endVertex = new GraphVertex('B');
|
const endVertex = new GraphVertex('B');
|
||||||
const edge = new GraphEdge(startVertex, endVertex);
|
const edge = new GraphEdge(startVertex, endVertex);
|
||||||
|
|
||||||
|
expect(edge.getKey()).toBe('A_B');
|
||||||
expect(edge.startVertex).toEqual(startVertex);
|
expect(edge.startVertex).toEqual(startVertex);
|
||||||
expect(edge.endVertex).toEqual(endVertex);
|
expect(edge.endVertex).toEqual(endVertex);
|
||||||
expect(edge.weight).toEqual(1);
|
expect(edge.weight).toEqual(1);
|
||||||
|
|||||||
Loading…
Reference in New Issue
Block a user