Add detect cycle.

README.md

@@ -68,7 +68,7 @@
   * [Breadth-First Search](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/breadth-first-search) (BFS)
   * [Dijkstra Algorithm](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/dijkstra) - finding shortest path to all graph vertices
   * [Bellman-Ford Algorithm](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/bellman-ford) - finding shortest path to all graph vertices
-  * Detect Cycle
+  * [Detect Cycle](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/detect-cycle)
   * Topological Sorting
   * Eulerian path, Eulerian circuit
   * Strongly Connected Component algorithm

src/algorithms/graph/detect-cycle/README.md

@@ -0,0 +1,60 @@
+# Detect Cycle in Graphs
+
+In graph theory, a **cycle** is a path of edges and vertices 
+wherein a vertex is reachable from itself. There are several 
+different types of cycles, principally a **closed walk** and 
+a **simple cycle**.
+
+## Definitions
+
+A **closed walk** consists of a sequence of vertices starting 
+and ending at the same vertex, with each two consecutive vertices
+in the sequence adjacent to each other in the graph. In a directed graph,
+each edge must be traversed by the walk consistently with its direction: 
+the edge must be oriented from the earlier of two consecutive vertices 
+to the later of the two vertices in the sequence. 
+The choice of starting vertex is not important: traversing the same cyclic 
+sequence of edges from different starting vertices produces the same closed walk.
+
+A **simple cycle may** be defined either as a closed walk with no repetitions of 
+vertices and edges allowed, other than the repetition of the starting and ending 
+vertex, or as the set of edges in such a walk. The two definitions are equivalent 
+in directed graphs, where simple cycles are also called directed cycles: the cyclic 
+sequence of vertices and edges in a walk is completely determined by the set of 
+edges that it uses. In undirected graphs the set of edges of a cycle can be 
+traversed by a walk in either of two directions, giving two possible directed cycles 
+for every undirected cycle. A circuit can be a closed walk allowing repetitions of 
+vertices but not edges; however, it can also be a simple cycle, so explicit 
+definition is recommended when it is used.
+
+## Example
+
+![Cycles](https://upload.wikimedia.org/wikipedia/commons/e/e7/Graph_cycle.gif)
+
+A graph with edges colored to illustrate **path** `H-A-B` (green), closed path or 
+**walk with a repeated vertex** `B-D-E-F-D-C-B` (blue) and a **cycle with no repeated edge** or 
+vertex `H-D-G-H` (red)
+
+### Cycle in undirected graph
+
+![Undirected Cycle](https://www.geeksforgeeks.org/wp-content/uploads/cycleGraph.png)
+
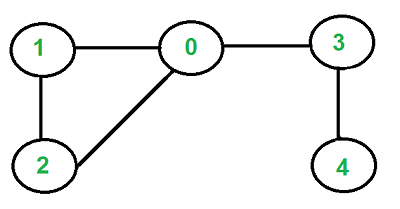
+### Cycle in directed graph
+
+![Directed Cycle](https://cdncontribute.geeksforgeeks.org/wp-content/uploads/cycle.png)
+
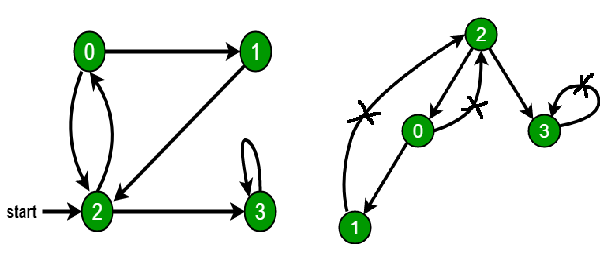
+## References
+
+General information:
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Cycle_(graph_theory))
+
+Cycles in undirected graphs:
+
+- [Detect Cycle in Undirected Graph on GeeksForGeeks](https://www.geeksforgeeks.org/detect-cycle-undirected-graph/)
+- [Detect Cycle in Undirected Graph Algorithm on YouTube](https://www.youtube.com/watch?v=n_t0a_8H8VY)
+
+Cycles in directed graphs:
+
+- [Detect Cycle in Directed Graph on GeeksForGeeks](https://www.geeksforgeeks.org/detect-cycle-in-a-graph/)
+- [Detect Cycle in Directed Graph Algorithm on YouTube](https://www.youtube.com/watch?v=rKQaZuoUR4M)

src/algorithms/graph/detect-cycle/__test__/detectUndirectedCycle.test.js

@@ -0,0 +1,36 @@
+import GraphVertex from '../../../../data-structures/graph/GraphVertex';
+import GraphEdge from '../../../../data-structures/graph/GraphEdge';
+import Graph from '../../../../data-structures/graph/Graph';
+import detectUndirectedCycle from '../detectUndirectedCycle';
+
+describe('detectUndirectedCycle', () => {
+  it('should detect undirected cycle', () => {
+    const vertexA = new GraphVertex('A');
+    const vertexB = new GraphVertex('B');
+    const vertexC = new GraphVertex('C');
+    const vertexD = new GraphVertex('D');
+    const vertexE = new GraphVertex('E');
+    const vertexF = new GraphVertex('F');
+
+    const edgeAF = new GraphEdge(vertexA, vertexF);
+    const edgeAB = new GraphEdge(vertexA, vertexB);
+    const edgeBE = new GraphEdge(vertexB, vertexE);
+    const edgeBC = new GraphEdge(vertexB, vertexC);
+    const edgeCD = new GraphEdge(vertexC, vertexD);
+    const edgeDE = new GraphEdge(vertexD, vertexE);
+
+    const graph = new Graph();
+    graph
+      .addEdge(edgeAF)
+      .addEdge(edgeAB)
+      .addEdge(edgeBE)
+      .addEdge(edgeBC)
+      .addEdge(edgeCD);
+
+    expect(detectUndirectedCycle(graph)).toBeFalsy();
+
+    graph.addEdge(edgeDE);
+
+    expect(detectUndirectedCycle(graph)).toBeTruthy();
+  });
+});

src/algorithms/graph/detect-cycle/detectUndirectedCycle.js

@@ -0,0 +1,32 @@
+import DisjointSet from '../../../data-structures/disjoint-set/DisjointSet';
+
+/**
+ * Detect cycle in undirected graph using disjoint sets.
+ *
+ * @param {Graph} graph
+ */
+
+export default function detectUndirectedCycle(graph) {
+  // Create initial singleton disjoint sets for each graph vertex.
+  /** @param {GraphVertex} graphVertex */
+  const keyExtractor = graphVertex => graphVertex.getKey();
+  const disjointSet = new DisjointSet(keyExtractor);
+  graph.getAllVertices().forEach(graphVertex => disjointSet.makeSet(graphVertex));
+
+  // Go trough all graph edges one by one and check if edge vertices are from the
+  // different sets. In this case joint those sets together. Do this until you find
+  // an edge where to edge vertices are already in one set. This means that current
+  // edge will create a cycle.
+  let cycleFound = false;
+  /** @param {GraphEdge} graphEdge */
+  graph.getAllEdges().forEach((graphEdge) => {
+    if (disjointSet.inSameSet(graphEdge.startVertex, graphEdge.endVertex)) {
+      // Cycle found.
+      cycleFound = true;
+    } else {
+      disjointSet.union(graphEdge.startVertex, graphEdge.endVertex);
+    }
+  });
+
+  return cycleFound;
+}

src/data-structures/graph/Graph.js

@@ -4,6 +4,7 @@ export default class Graph {
    */
   constructor(isDirected = false) {
     this.vertices = {};
+    this.edges = {};
     this.isDirected = isDirected;
   }
 
@@ -39,6 +40,13 @@ export default class Graph {
     return Object.values(this.vertices);
   }
 
+  /**
+   * @return {GraphEdge[]}
+   */
+  getAllEdges() {
+    return Object.values(this.edges);
+  }
+
   /**
    * @param {GraphEdge} edge
    * @returns {Graph}
@@ -60,7 +68,12 @@ export default class Graph {
       endVertex = this.getVertexByKey(edge.endVertex.getKey());
     }
 
-    // @TODO: Check if edge has been already added.
+    // Check if edge has been already added.
+    if (this.edges[edge.getKey()]) {
+      throw new Error('Edge has already been added before');
+    } else {
+      this.edges[edge.getKey()] = edge;
+    }
 
     // Add edge to the vertices.
     if (this.isDirected) {

src/data-structures/graph/GraphEdge.js

@@ -9,4 +9,14 @@ export default class GraphEdge {
     this.endVertex = endVertex;
     this.weight = weight;
   }
+
+  /**
+   * @return {string}
+   */
+  getKey() {
+    const startVertexKey = this.startVertex.getKey();
+    const endVertexKey = this.endVertex.getKey();
+
+    return `${startVertexKey}_${endVertexKey}`;
+  }
 }

src/data-structures/graph/__test__/Graph.test.js

@@ -136,4 +136,42 @@ describe('Graph', () => {
     expect(neighbors[0]).toEqual(vertexB);
     expect(neighbors[1]).toEqual(vertexC);
   });
+
+  it('should throw an error when trying to add edge twice', () => {
+    function addSameEdgeTwice() {
+      const graph = new Graph(true);
+
+      const vertexA = new GraphVertex('A');
+      const vertexB = new GraphVertex('B');
+
+      const edgeAB = new GraphEdge(vertexA, vertexB);
+
+      graph
+        .addEdge(edgeAB)
+        .addEdge(edgeAB);
+    }
+
+    expect(addSameEdgeTwice).toThrow();
+  });
+
+  it('should return the list of all added edges', () => {
+    const graph = new Graph(true);
+
+    const vertexA = new GraphVertex('A');
+    const vertexB = new GraphVertex('B');
+    const vertexC = new GraphVertex('C');
+
+    const edgeAB = new GraphEdge(vertexA, vertexB);
+    const edgeBC = new GraphEdge(vertexB, vertexC);
+
+    graph
+      .addEdge(edgeAB)
+      .addEdge(edgeBC);
+
+    const edges = graph.getAllEdges();
+
+    expect(edges.length).toBe(2);
+    expect(edges[0]).toEqual(edgeAB);
+    expect(edges[1]).toEqual(edgeBC);
+  });
 });

src/data-structures/graph/__test__/GraphEdge.test.js

@@ -7,6 +7,7 @@ describe('GraphEdge', () => {
     const endVertex = new GraphVertex('B');
     const edge = new GraphEdge(startVertex, endVertex);
 
+    expect(edge.getKey()).toBe('A_B');
     expect(edge.startVertex).toEqual(startVertex);
     expect(edge.endVertex).toEqual(endVertex);
     expect(edge.weight).toEqual(1);