mirror of
https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git
synced 2024-12-26 23:21:18 +08:00
Add primality tests.
This commit is contained in:
parent
54f6aadec4
commit
4fc5483892
@ -31,10 +31,10 @@
|
|||||||
* [Fibonacci Number](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/fibonacci)
|
* [Fibonacci Number](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/fibonacci)
|
||||||
* [Cartesian Product](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/cartesian-product)
|
* [Cartesian Product](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/cartesian-product)
|
||||||
* [Power Set](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/power-set)
|
* [Power Set](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/power-set)
|
||||||
* [Primality Test](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/primality-test)
|
* [Primality Test](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/primality-test) (Trial Division)
|
||||||
|
* [Euclidean Algorithm](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/euclidean-algorithm) - calculate the greatest common divisor (GCD)
|
||||||
* Collatz Conjecture algorithm
|
* Collatz Conjecture algorithm
|
||||||
* Extended Euclidean algorithm
|
* Extended Euclidean algorithm
|
||||||
* Euclidean algorithm to calculate the Greatest Common Divisor (GCD)
|
|
||||||
* Find Divisors
|
* Find Divisors
|
||||||
* Fisher-Yates
|
* Fisher-Yates
|
||||||
* Greatest Difference
|
* Greatest Difference
|
||||||
|
|||||||
57
src/algorithms/math/euclidean-algorithm/README.md
Normal file
57
src/algorithms/math/euclidean-algorithm/README.md
Normal file
@ -0,0 +1,57 @@
|
|||||||
|
# Euclidean algorithm
|
||||||
|
|
||||||
|
In mathematics, the Euclidean algorithm, or Euclid's algorithm,
|
||||||
|
is an efficient method for computing the greatest common divisor
|
||||||
|
(GCD) of two numbers, the largest number that divides both of
|
||||||
|
them without leaving a remainder.
|
||||||
|
|
||||||
|
The Euclidean algorithm is based on the principle that the
|
||||||
|
greatest common divisor of two numbers does not change if
|
||||||
|
the larger number is replaced by its difference with the
|
||||||
|
smaller number. For example, `21` is the GCD of `252` and
|
||||||
|
`105` (as `252 = 21 × 12` and `105 = 21 × 5`), and the same
|
||||||
|
number `21` is also the GCD of `105` and `252 − 105 = 147`.
|
||||||
|
Since this replacement reduces the larger of the two numbers,
|
||||||
|
repeating this process gives successively smaller pairs of
|
||||||
|
numbers until the two numbers become equal.
|
||||||
|
When that occurs, they are the GCD of the original two numbers.
|
||||||
|
|
||||||
|
By reversing the steps, the GCD can be expressed as a sum of
|
||||||
|
the two original numbers each multiplied by a positive or
|
||||||
|
negative integer, e.g., `21 = 5 × 105 + (−2) × 252`.
|
||||||
|
The fact that the GCD can always be expressed in this way is
|
||||||
|
known as Bézout's identity.
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
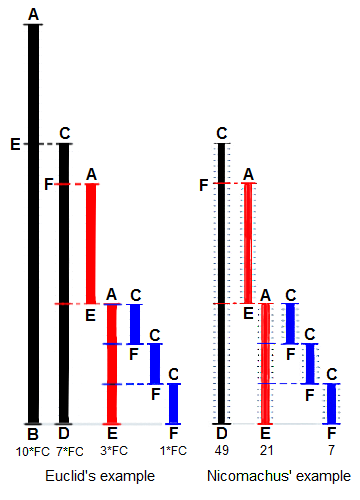
Euclid's method for finding the greatest common divisor (GCD)
|
||||||
|
of two starting lengths `BA` and `DC`, both defined to be
|
||||||
|
multiples of a common "unit" length. The length `DC` being
|
||||||
|
shorter, it is used to "measure" `BA`, but only once because
|
||||||
|
remainder `EA` is less than `DC`. EA now measures (twice)
|
||||||
|
the shorter length `DC`, with remainder `FC` shorter than `EA`.
|
||||||
|
Then `FC` measures (three times) length `EA`. Because there is
|
||||||
|
no remainder, the process ends with `FC` being the `GCD`.
|
||||||
|
On the right Nicomachus' example with numbers `49` and `21`
|
||||||
|
resulting in their GCD of `7` (derived from Heath 1908:300).
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
A `24-by-60` rectangle is covered with ten `12-by-12` square
|
||||||
|
tiles, where `12` is the GCD of `24` and `60`. More generally,
|
||||||
|
an `a-by-b` rectangle can be covered with square tiles of
|
||||||
|
side-length `c` only if `c` is a common divisor of `a` and `b`.
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
Subtraction-based animation of the Euclidean algorithm.
|
||||||
|
The initial rectangle has dimensions `a = 1071` and `b = 462`.
|
||||||
|
Squares of size `462×462` are placed within it leaving a
|
||||||
|
`462×147` rectangle. This rectangle is tiled with `147×147`
|
||||||
|
squares until a `21×147` rectangle is left, which in turn is
|
||||||
|
tiled with `21×21` squares, leaving no uncovered area.
|
||||||
|
The smallest square size, `21`, is the GCD of `1071` and `462`.
|
||||||
|
|
||||||
|
## References
|
||||||
|
|
||||||
|
[Wikipedia](https://en.wikipedia.org/wiki/Euclidean_algorithm)
|
||||||
@ -0,0 +1,24 @@
|
|||||||
|
import euclideanAlgorithm from '../euclideanAlgorithm';
|
||||||
|
|
||||||
|
describe('euclideanAlgorithm', () => {
|
||||||
|
it('should calculate GCD', () => {
|
||||||
|
expect(euclideanAlgorithm(0, 0)).toBeNull();
|
||||||
|
expect(euclideanAlgorithm(2, 0)).toBe(2);
|
||||||
|
expect(euclideanAlgorithm(0, 2)).toBe(2);
|
||||||
|
expect(euclideanAlgorithm(1, 2)).toBe(1);
|
||||||
|
expect(euclideanAlgorithm(2, 1)).toBe(1);
|
||||||
|
expect(euclideanAlgorithm(6, 6)).toBe(6);
|
||||||
|
expect(euclideanAlgorithm(2, 4)).toBe(2);
|
||||||
|
expect(euclideanAlgorithm(4, 2)).toBe(2);
|
||||||
|
expect(euclideanAlgorithm(12, 4)).toBe(4);
|
||||||
|
expect(euclideanAlgorithm(4, 12)).toBe(4);
|
||||||
|
expect(euclideanAlgorithm(5, 13)).toBe(1);
|
||||||
|
expect(euclideanAlgorithm(27, 13)).toBe(1);
|
||||||
|
expect(euclideanAlgorithm(24, 60)).toBe(12);
|
||||||
|
expect(euclideanAlgorithm(60, 24)).toBe(12);
|
||||||
|
expect(euclideanAlgorithm(252, 105)).toBe(21);
|
||||||
|
expect(euclideanAlgorithm(105, 252)).toBe(21);
|
||||||
|
expect(euclideanAlgorithm(1071, 462)).toBe(21);
|
||||||
|
expect(euclideanAlgorithm(462, 1071)).toBe(21);
|
||||||
|
});
|
||||||
|
});
|
||||||
@ -0,0 +1,24 @@
|
|||||||
|
/**
|
||||||
|
* @param {number} a
|
||||||
|
* @param {number} b
|
||||||
|
* @return {number|null}
|
||||||
|
*/
|
||||||
|
export default function euclideanAlgorithm(a, b) {
|
||||||
|
if (a === 0 && b === 0) {
|
||||||
|
return null;
|
||||||
|
}
|
||||||
|
|
||||||
|
if (a === 0 && b !== 0) {
|
||||||
|
return b;
|
||||||
|
}
|
||||||
|
|
||||||
|
if (a !== 0 && b === 0) {
|
||||||
|
return a;
|
||||||
|
}
|
||||||
|
|
||||||
|
if (a > b) {
|
||||||
|
return euclideanAlgorithm(a - b, b);
|
||||||
|
}
|
||||||
|
|
||||||
|
return euclideanAlgorithm(b - a, a);
|
||||||
|
}
|
||||||
Loading…
Reference in New Issue
Block a user