Add Tarjan's algorithm.

README.md

@@ -72,7 +72,8 @@
   * [Prim’s Algorithm](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/prim) - finding Minimum Spanning Tree (MST) for weighted undirected graph
   * [Kruskal’s Algorithm](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/kruskal) - finding Minimum Spanning Tree (MST) for weighted undirected graph
   * [Topological Sorting](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/topological-sorting) - DFS method
-  * Eulerian path, Eulerian circuit
+  * [Articulation Points](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/articulation-points) - Tarjan's algorithm
+  * [Eulerian Path and Eulerian Circuit](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/graph/eulerian-path)
   * Strongly Connected Component algorithm
   * Shortest Path Faster Algorithm (SPFA)
 * **Uncategorized**  

src/algorithms/graph/articulation-points/README.md

@@ -0,0 +1,22 @@
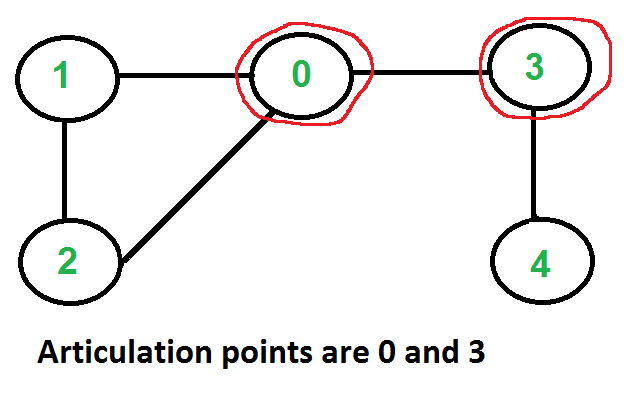
+# Articulation Points (or Cut Vertices)
+
+A vertex in an undirected connected graph is an articulation point
+(or cut vertex) iff removing it (and edges through it) disconnects 
+the graph. Articulation points represent vulnerabilities in a 
+connected network – single points whose failure would split the 
+network into 2 or more disconnected components. They are useful for 
+designing reliable networks.
+
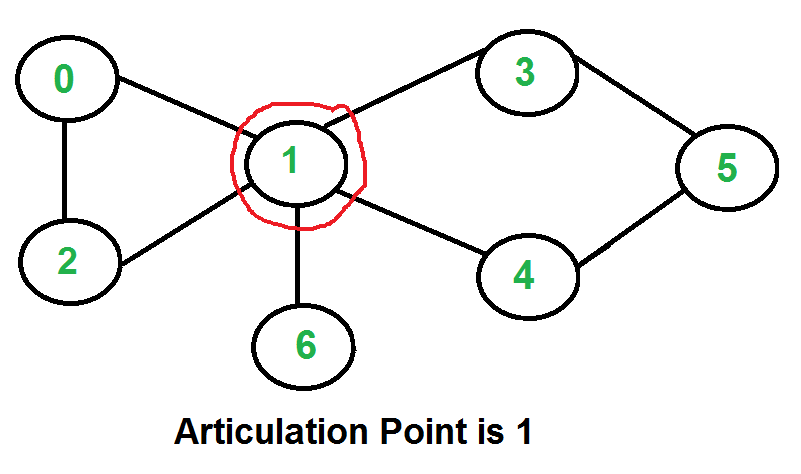
+For a disconnected undirected graph, an articulation point is a 
+vertex removing which increases number of connected components.
+
+![Articulation Points](https://www.geeksforgeeks.org/wp-content/uploads/ArticulationPoints.png)
+
+![Articulation Points](https://www.geeksforgeeks.org/wp-content/uploads/ArticulationPoints1.png)
+
+![Articulation Points](https://www.geeksforgeeks.org/wp-content/uploads/ArticulationPoints21.png)
+
+## References
+
+- [GeeksForGeeks](https://www.geeksforgeeks.org/articulation-points-or-cut-vertices-in-a-graph/)
+- [YouTube](https://www.youtube.com/watch?v=2kREIkF9UAs)

src/algorithms/graph/articulation-points/__test__/articulationPoints.test.js

@@ -0,0 +1,143 @@
+import GraphVertex from '../../../../data-structures/graph/GraphVertex';
+import GraphEdge from '../../../../data-structures/graph/GraphEdge';
+import Graph from '../../../../data-structures/graph/Graph';
+import articulationPoints from '../articulationPoints';
+
+describe('articulationPoints', () => {
+  it('should find articulation points in simple graph', () => {
+    const vertexA = new GraphVertex('A');
+    const vertexB = new GraphVertex('B');
+    const vertexC = new GraphVertex('C');
+    const vertexD = new GraphVertex('D');
+
+    const edgeAB = new GraphEdge(vertexA, vertexB);
+    const edgeBC = new GraphEdge(vertexB, vertexC);
+    const edgeCD = new GraphEdge(vertexC, vertexD);
+
+    const graph = new Graph();
+
+    graph
+      .addEdge(edgeAB)
+      .addEdge(edgeBC)
+      .addEdge(edgeCD);
+
+    const articulationPointsSet = articulationPoints(graph);
+
+    expect(articulationPointsSet).toEqual([
+      vertexC,
+      vertexB,
+    ]);
+  });
+
+  it('should find articulation points in simple graph with back edge', () => {
+    const vertexA = new GraphVertex('A');
+    const vertexB = new GraphVertex('B');
+    const vertexC = new GraphVertex('C');
+    const vertexD = new GraphVertex('D');
+
+    const edgeAB = new GraphEdge(vertexA, vertexB);
+    const edgeBC = new GraphEdge(vertexB, vertexC);
+    const edgeCD = new GraphEdge(vertexC, vertexD);
+    const edgeAC = new GraphEdge(vertexA, vertexC);
+
+    const graph = new Graph();
+
+    graph
+      .addEdge(edgeAB)
+      .addEdge(edgeAC)
+      .addEdge(edgeBC)
+      .addEdge(edgeCD);
+
+    const articulationPointsSet = articulationPoints(graph);
+
+    expect(articulationPointsSet).toEqual([
+      vertexC,
+    ]);
+  });
+
+  it('should find articulation points in graph', () => {
+    const vertexA = new GraphVertex('A');
+    const vertexB = new GraphVertex('B');
+    const vertexC = new GraphVertex('C');
+    const vertexD = new GraphVertex('D');
+    const vertexE = new GraphVertex('E');
+    const vertexF = new GraphVertex('F');
+    const vertexG = new GraphVertex('G');
+    const vertexH = new GraphVertex('H');
+
+    const edgeAB = new GraphEdge(vertexA, vertexB);
+    const edgeBC = new GraphEdge(vertexB, vertexC);
+    const edgeAC = new GraphEdge(vertexA, vertexC);
+    const edgeCD = new GraphEdge(vertexC, vertexD);
+    const edgeDE = new GraphEdge(vertexD, vertexE);
+    const edgeEG = new GraphEdge(vertexE, vertexG);
+    const edgeEF = new GraphEdge(vertexE, vertexF);
+    const edgeGF = new GraphEdge(vertexG, vertexF);
+    const edgeFH = new GraphEdge(vertexF, vertexH);
+
+    const graph = new Graph();
+
+    graph
+      .addEdge(edgeAB)
+      .addEdge(edgeBC)
+      .addEdge(edgeAC)
+      .addEdge(edgeCD)
+      .addEdge(edgeDE)
+      .addEdge(edgeEG)
+      .addEdge(edgeEF)
+      .addEdge(edgeGF)
+      .addEdge(edgeFH);
+
+    const articulationPointsSet = articulationPoints(graph);
+
+    expect(articulationPointsSet).toEqual([
+      vertexF,
+      vertexE,
+      vertexD,
+      vertexC,
+    ]);
+  });
+
+  it('should find articulation points in graph starting with articulation root vertex', () => {
+    const vertexA = new GraphVertex('A');
+    const vertexB = new GraphVertex('B');
+    const vertexC = new GraphVertex('C');
+    const vertexD = new GraphVertex('D');
+    const vertexE = new GraphVertex('E');
+    const vertexF = new GraphVertex('F');
+    const vertexG = new GraphVertex('G');
+    const vertexH = new GraphVertex('H');
+
+    const edgeAB = new GraphEdge(vertexA, vertexB);
+    const edgeBC = new GraphEdge(vertexB, vertexC);
+    const edgeAC = new GraphEdge(vertexA, vertexC);
+    const edgeCD = new GraphEdge(vertexC, vertexD);
+    const edgeDE = new GraphEdge(vertexD, vertexE);
+    const edgeEG = new GraphEdge(vertexE, vertexG);
+    const edgeEF = new GraphEdge(vertexE, vertexF);
+    const edgeGF = new GraphEdge(vertexG, vertexF);
+    const edgeFH = new GraphEdge(vertexF, vertexH);
+
+    const graph = new Graph();
+
+    graph
+      .addEdge(edgeDE)
+      .addEdge(edgeAB)
+      .addEdge(edgeBC)
+      .addEdge(edgeAC)
+      .addEdge(edgeCD)
+      .addEdge(edgeEG)
+      .addEdge(edgeEF)
+      .addEdge(edgeGF)
+      .addEdge(edgeFH);
+
+    const articulationPointsSet = articulationPoints(graph);
+
+    expect(articulationPointsSet).toEqual([
+      vertexF,
+      vertexE,
+      vertexC,
+      vertexD,
+    ]);
+  });
+});

src/algorithms/graph/articulation-points/articulationPoints.js

@@ -0,0 +1,116 @@
+import depthFirstSearch from '../depth-first-search/depthFirstSearch';
+
+/**
+ * Helper class for visited vertex metadata.
+ */
+class VisitMetadata {
+  constructor({ discoveryTime, lowDiscoveryTime }) {
+    this.discoveryTime = discoveryTime;
+    this.lowDiscoveryTime = lowDiscoveryTime;
+
+    // We need this to know to which vertex we need to compare discovery time
+    // when leaving the vertex.
+    this.childVertex = null;
+
+    // We need this in order to check graph root node, whether it has two
+    // disconnected children or not.
+    this.childrenCount = 0;
+  }
+}
+
+/**
+ * Tarjan's algorithm for rinding articulation points in graph.
+ *
+ * @param {Graph} graph
+ * @return {GraphVertex[]}
+ */
+export default function articulationPoints(graph) {
+  // Set of vertices we've already visited during DFS.
+  const visitedSet = {};
+
+  // Set of articulation points found so far.
+  const articulationPointsSet = [];
+
+  // Time needed to get to the current vertex.
+  let discoveryTime = 0;
+
+  // Peek the start vertex for DFS traversal.
+  const startVertex = graph.getAllVertices()[0];
+
+  const dfsCallbacks = {
+    /**
+     * @param {GraphVertex} currentVertex
+     * @param {GraphVertex} previousVertex
+     */
+    enterVertex: ({ currentVertex, previousVertex }) => {
+      // Put current vertex to visited set.
+      visitedSet[currentVertex.getKey()] = new VisitMetadata({
+        discoveryTime,
+        lowDiscoveryTime: discoveryTime,
+      });
+
+      // Tick discovery time.
+      discoveryTime += 1;
+
+      if (previousVertex) {
+        // Update child vertex information for previous vertex.
+        visitedSet[previousVertex.getKey()].childVertex = currentVertex;
+
+        // Update children counter for previous vertex.
+        visitedSet[previousVertex.getKey()].childrenCount += 1;
+      }
+    },
+    /**
+     * @param {GraphVertex} currentVertex
+     * @param {GraphVertex} previousVertex
+     */
+    leaveVertex: ({ currentVertex }) => {
+      // Detect whether current vertex is articulation point or not.
+      // To do so we need to check two (OR) conditions:
+      // 1. Is it a root vertex with at least two independent children.
+      // 2. If its visited time is <= low time of adjacent vertex.
+      if (currentVertex === startVertex) {
+        // Check that it has at least two independent children.
+        if (visitedSet[currentVertex.getKey()].childrenCount >= 2) {
+          articulationPointsSet.push(currentVertex);
+        }
+      } else {
+        // Get child vertex low discovery time.
+        let childVertexLowDiscoveryTime = null;
+        if (visitedSet[currentVertex.getKey()].childVertex) {
+          const childVertexKey = visitedSet[currentVertex.getKey()].childVertex.getKey();
+          childVertexLowDiscoveryTime = visitedSet[childVertexKey].lowDiscoveryTime;
+        }
+
+        // Compare child vertex low discovery time with current discovery time to if there
+        // are any short path (back edge) exists. If we can get to child vertex faster then
+        // to current one it means that there is a back edge exists (short path) and current
+        // vertex isn't articulation point.
+        const currentDiscoveryTime = visitedSet[currentVertex.getKey()].discoveryTime;
+        if (currentDiscoveryTime <= childVertexLowDiscoveryTime) {
+          articulationPointsSet.push(currentVertex);
+        }
+
+        // Update the low time with the smallest time of adjacent vertices.
+
+        // Get minimum low discovery time from all neighbors.
+        /** @param {GraphVertex} neighbor */
+        visitedSet[currentVertex.getKey()].lowDiscoveryTime = currentVertex.getNeighbors().reduce(
+          (lowestDiscoveryTime, neighbor) => {
+            const neighborLowTime = visitedSet[neighbor.getKey()].lowDiscoveryTime;
+            return neighborLowTime < lowestDiscoveryTime ? neighborLowTime : lowestDiscoveryTime;
+          },
+          visitedSet[currentVertex.getKey()].lowDiscoveryTime,
+        );
+      }
+    },
+    allowTraversal: ({ nextVertex }) => {
+      return !visitedSet[nextVertex.getKey()];
+    },
+  };
+
+  // Do Depth First Search traversal over submitted graph.
+  depthFirstSearch(graph, startVertex, dfsCallbacks);
+
+  return articulationPointsSet;
+}

src/algorithms/graph/eulerian-path/README.md

@@ -0,0 +1,34 @@
+# Eulerian Path
+
+In graph theory, an **Eulerian trail** (or **Eulerian path**) is a 
+trail in a finite graph which visits every edge exactly once.
+Similarly, an **Eulerian circuit** or **Eulerian cycle** is an 
+Eulerian trail which starts and ends on the same vertex.
+
+Euler proved that a necessary condition for the existence of Eulerian 
+circuits is that all vertices in the graph have an even degree, and 
+stated that connected graphs with all vertices of even degree have 
+an Eulerian circuit.
+
+![Eulerian Circuit](https://upload.wikimedia.org/wikipedia/commons/7/72/Labelled_Eulergraph.svg)
+
+Every vertex of this graph has an even degree. Therefore, this is 
+an Eulerian graph. Following the edges in alphabetical order gives 
+an Eulerian circuit/cycle.
+
+For the existence of Eulerian trails it is necessary that zero or 
+two vertices have an odd degree; this means the Königsberg graph 
+is not Eulerian. If there are no vertices of odd degree, 
+all Eulerian trails are circuits. If there are exactly two vertices 
+of odd degree, all Eulerian trails start at one of them and end at 
+the other. A graph that has an Eulerian trail but not an Eulerian 
+circuit is called semi-Eulerian.
+
+![Königsberg graph](https://upload.wikimedia.org/wikipedia/commons/9/96/K%C3%B6nigsberg_graph.svg)
+
+The Königsberg Bridges multigraph. This multigraph is not Eulerian, 
+therefore, a solution does not exist.
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Eulerian_path)