mirror of
https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git
synced 2024-12-25 22:46:20 +08:00
Add factorial.
This commit is contained in:
parent
4434e96413
commit
77e897b3b9
@ -28,6 +28,7 @@
|
||||
### Algorithms
|
||||
|
||||
* **Math**
|
||||
* [Factorial](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/factorial)
|
||||
* [Fibonacci Number](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/fibonacci)
|
||||
* [Cartesian Product](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/cartesian-product)
|
||||
* [Power Set](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/power-set)
|
||||
@ -37,7 +38,7 @@
|
||||
* [Fisher–Yates Shuffle](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/math/fisher-yates) - random permutation of a finite sequence
|
||||
* **String**
|
||||
* [Permutations](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/string/permutations) (with and without repetitions)
|
||||
* Combination
|
||||
* [Combinations](https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/string/combinations) (with and without repetitions)
|
||||
* Minimum Edit distance (Levenshtein Distance)
|
||||
* Hamming
|
||||
* Huffman
|
||||
|
||||
32
src/algorithms/math/factorial/README.md
Normal file
32
src/algorithms/math/factorial/README.md
Normal file
@ -0,0 +1,32 @@
|
||||
# Factorial
|
||||
|
||||
In mathematics, the factorial of a non-negative integer `n`,
|
||||
denoted by `n!`, is the product of all positive integers less
|
||||
than or equal to `n`. For example:
|
||||
|
||||
```
|
||||
5! = 5 * 4 * 3 * 2 * 1 = 120
|
||||
```
|
||||
|
||||
| n | n! |
|
||||
| ----- | :-------------------------: |
|
||||
| 0 | 1 |
|
||||
| 1 | 1 |
|
||||
| 2 | 2 |
|
||||
| 3 | 6 |
|
||||
| 4 | 24 |
|
||||
| 5 | 120 |
|
||||
| 6 | 720 |
|
||||
| 7 | 5 040 |
|
||||
| 8 | 40 320 |
|
||||
| 9 | 362 880 |
|
||||
| 10 | 3 628 800 |
|
||||
| 11 | 39 916 800 |
|
||||
| 12 | 479 001 600 |
|
||||
| 13 | 6 227 020 800 |
|
||||
| 14 | 87 178 291 200 |
|
||||
| 15 | 1 307 674 368 000 |
|
||||
|
||||
## References
|
||||
|
||||
[Wikipedia](https://en.wikipedia.org/wiki/Factorial)
|
||||
11
src/algorithms/math/factorial/__test__/factorial.test.js
Normal file
11
src/algorithms/math/factorial/__test__/factorial.test.js
Normal file
@ -0,0 +1,11 @@
|
||||
import factorial from '../factorial';
|
||||
|
||||
describe('factorial', () => {
|
||||
it('should calculate factorial', () => {
|
||||
expect(factorial(0)).toBe(1);
|
||||
expect(factorial(1)).toBe(1);
|
||||
expect(factorial(5)).toBe(120);
|
||||
expect(factorial(8)).toBe(40320);
|
||||
expect(factorial(10)).toBe(3628800);
|
||||
});
|
||||
});
|
||||
13
src/algorithms/math/factorial/factorial.js
Normal file
13
src/algorithms/math/factorial/factorial.js
Normal file
@ -0,0 +1,13 @@
|
||||
/**
|
||||
* @param {number} number
|
||||
* @return {number}
|
||||
*/
|
||||
export default function factorial(number) {
|
||||
let result = 1;
|
||||
|
||||
for (let i = 1; i <= number; i += 1) {
|
||||
result *= i;
|
||||
}
|
||||
|
||||
return result;
|
||||
}
|
||||
@ -11,8 +11,45 @@ its the same fruit salad.
|
||||
|
||||
## Combinations without repetitions
|
||||
|
||||
This is how lotteries work. The numbers are drawn one at a
|
||||
time, and if we have the lucky numbers (no matter what order)
|
||||
we win!
|
||||
|
||||
No Repetition: such as lottery numbers `(2,14,15,27,30,33)`
|
||||
|
||||
**Number of combinations**
|
||||
|
||||
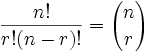
|
||||
|
||||
where `n` is the number of things to choose from, and we choose `r` of them,
|
||||
no repetition, order doesn't matter.
|
||||
|
||||
It is often called "n choose r" (such as "16 choose 3"). And is also known as the Binomial Coefficient.
|
||||
|
||||
## Combinations with repetitions
|
||||
|
||||
Repetition is Allowed: such as coins in your pocket `(5,5,5,10,10)`
|
||||
|
||||
Or let us say there are five flavours of icecream:
|
||||
`banana`, `chocolate`, `lemon`, `strawberry` and `vanilla`.
|
||||
|
||||
We can have three scoops. How many variations will there be?
|
||||
|
||||
Let's use letters for the flavours: `{b, c, l, s, v}`.
|
||||
Example selections include:
|
||||
|
||||
- `{c, c, c}` (3 scoops of chocolate)
|
||||
- `{b, l, v}` (one each of banana, lemon and vanilla)
|
||||
- `{b, v, v}` (one of banana, two of vanilla)
|
||||
|
||||
**Number of combinations**
|
||||
|
||||
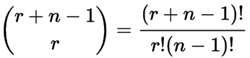
|
||||
|
||||
Where `n` is the number of things to choose from, and we
|
||||
choose `r` of them. Repetition allowed,
|
||||
order doesn't matter.
|
||||
|
||||
## References
|
||||
|
||||
[Math Is Fun](https://www.mathsisfun.com/combinatorics/combinations-permutations.html)
|
||||
|
||||
Loading…
Reference in New Issue
Block a user