Adding K Nearest Neighbor to ML folder in algorithms with README and tests (#592)

* Updated KNN and README

* Update README.md

* new

* new

* updated tests

* updated knn coverage

README.md

@@ -23,7 +23,7 @@ _Read this in other languages:_
 [_Türk_](README.tr-TR.md),
 [_Italiana_](README.it-IT.md)
 
-*☝ Note that this project is meant to be used for learning and researching purposes 
+*☝ Note that this project is meant to be used for learning and researching purposes
 only, and it is **not** meant to be used for production.*
 
 ## Data Structures
@@ -64,7 +64,7 @@ a set of rules that precisely define a sequence of operations.
 
 * **Math**
   * `B` [Bit Manipulation](src/algorithms/math/bits) - set/get/update/clear bits, multiplication/division by two, make negative etc.
-  * `B` [Factorial](src/algorithms/math/factorial) 
+  * `B` [Factorial](src/algorithms/math/factorial)
   * `B` [Fibonacci Number](src/algorithms/math/fibonacci) - classic and closed-form versions
   * `B` [Prime Factors](src/algorithms/math/prime-factors) - finding prime factors and counting them using Hardy-Ramanujan's theorem  
   * `B` [Primality Test](src/algorithms/math/primality-test) (trial division method)
@@ -80,7 +80,7 @@ a set of rules that precisely define a sequence of operations.
   * `A` [Integer Partition](src/algorithms/math/integer-partition)
   * `A` [Square Root](src/algorithms/math/square-root) - Newton's method
   * `A` [Liu Hui π Algorithm](src/algorithms/math/liu-hui) - approximate π calculations based on N-gons
-  * `A` [Discrete Fourier Transform](src/algorithms/math/fourier-transform) - decompose a function of time (a signal) into the frequencies that make it up 
+  * `A` [Discrete Fourier Transform](src/algorithms/math/fourier-transform) - decompose a function of time (a signal) into the frequencies that make it up
 * **Sets**
   * `B` [Cartesian Product](src/algorithms/sets/cartesian-product) - product of multiple sets
   * `B` [Fisher–Yates Shuffle](src/algorithms/sets/fisher-yates) - random permutation of a finite sequence
@@ -142,12 +142,13 @@ a set of rules that precisely define a sequence of operations.
   * `B` [Polynomial Hash](src/algorithms/cryptography/polynomial-hash) - rolling hash function based on polynomial
   * `B` [Caesar Cipher](src/algorithms/cryptography/caesar-cipher) - simple substitution cipher
 * **Machine Learning**
-  * `B` [NanoNeuron](https://github.com/trekhleb/nano-neuron) - 7 simple JS functions that illustrate how machines can actually learn (forward/backward propagation)
+  * `B` [NanoNeuron](https://github.com/trekhleb/nano-neuron) - 7 simple JS functions that illustrate how machines can actually learn (forward/backward propagation)  
+  * `B` [KNN](src/algorithms/ML/KNN) - K Nearest Neighbors
 * **Uncategorized**
   * `B` [Tower of Hanoi](src/algorithms/uncategorized/hanoi-tower)
   * `B` [Square Matrix Rotation](src/algorithms/uncategorized/square-matrix-rotation) - in-place algorithm
-  * `B` [Jump Game](src/algorithms/uncategorized/jump-game) - backtracking, dynamic programming (top-down + bottom-up) and greedy examples 
-  * `B` [Unique Paths](src/algorithms/uncategorized/unique-paths) - backtracking, dynamic programming and Pascal's Triangle based examples 
+  * `B` [Jump Game](src/algorithms/uncategorized/jump-game) - backtracking, dynamic programming (top-down + bottom-up) and greedy examples
+  * `B` [Unique Paths](src/algorithms/uncategorized/unique-paths) - backtracking, dynamic programming and Pascal's Triangle based examples
   * `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - trapping rain water problem (dynamic programming and brute force versions)
   * `B` [Recursive Staircase](src/algorithms/uncategorized/recursive-staircase) - count the number of ways to reach to the top (4 solutions)
   * `A` [N-Queens Problem](src/algorithms/uncategorized/n-queens)

src/algorithms/ML/KNN/README.md

@@ -0,0 +1,23 @@
+# KNN Algorithm  
+
+KNN stands for K Nearest Neighbors. KNN is a supervised Machine Learning algorithm. It's a classification algorithm, determining the class of a sample vector using a sample data.  
+
+The idea is to calculate the similarity between two data points on the basis of a distance metric. Euclidean distance is used mostly for this task. The algorithm is as follows -  
+
+1. Check for errors like invalid data/labels.
+2. Calculate the euclidean distance of all the data points in training data with the classification point
+3. Sort the distances of points along with their classes in ascending order
+4. Take the initial "K" classes and find the mode to get the most similar class
+5. Report the most similar class  
+
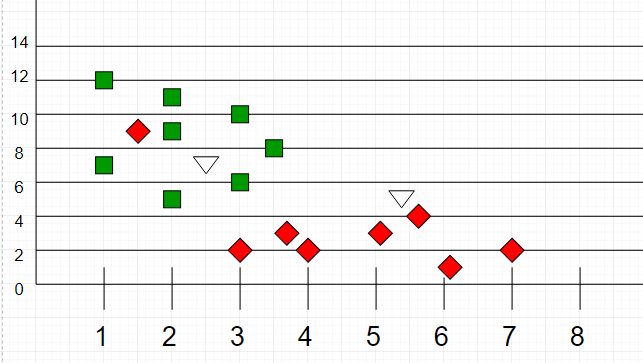
+Here is a visualization for better understanding -  
+
+![KNN Visualization](https://media.geeksforgeeks.org/wp-content/uploads/graph2-2.png)  
+
+Here, as we can see, the classification of unknown points will be judged by their proximity to other points.
+
+It is important to note that "K" is preferred to have odd values in order to break ties. Usually "K" is taken as 3 or 5.  
+
+## References
+
+- [GeeksforGeeks](https://media.geeksforgeeks.org/wp-content/uploads/graph2-2.png)

src/algorithms/ML/KNN/__test__/knn.test.js

@@ -0,0 +1,42 @@
+import KNN from '../knn';
+
+describe('KNN', () => {
+  test('should throw an error on invalid data', () => {
+    expect(() => {
+      KNN();
+    }).toThrowError();
+  });
+  test('should throw an error on invalid labels', () => {
+    const nolabels = () => {
+      KNN([[1, 1]]);
+    };
+    expect(nolabels).toThrowError();
+  });
+  it('should throw an error on not giving classification vector', () => {
+    const noclassification = () => {
+      KNN([[1, 1]], [1]);
+    };
+    expect(noclassification).toThrowError();
+  });
+  it('should throw an error on not giving classification vector', () => {
+    const inconsistent = () => {
+      KNN([[1, 1]], [1], [1]);
+    };
+    expect(inconsistent).toThrowError();
+  });
+  it('should find the nearest neighbour', () => {
+    let dataX = [[1, 1], [2, 2]];
+    let dataY = [1, 2];
+    expect(KNN(dataX, dataY, [1, 1])).toBe(1);
+
+    dataX = [[1, 1], [6, 2], [3, 3], [4, 5], [9, 2], [2, 4], [8, 7]];
+    dataY = [1, 2, 1, 2, 1, 2, 1];
+    expect(KNN(dataX, dataY, [1.25, 1.25]))
+      .toBe(1);
+
+    dataX = [[1, 1], [6, 2], [3, 3], [4, 5], [9, 2], [2, 4], [8, 7]];
+    dataY = [1, 2, 1, 2, 1, 2, 1];
+    expect(KNN(dataX, dataY, [1.25, 1.25], 5))
+      .toBe(2);
+  });
+});

src/algorithms/ML/KNN/knn.js

@@ -0,0 +1,60 @@
+/**
+ * @param {object} dataY
+ * @param {object} dataX
+ * @param {object} toClassify
+ * @param {number} k
+ * @return {number}
+ */
+export default function KNN(dataX, dataY, toClassify, K) {
+  let k = -1;
+
+  if (K === undefined) {
+    k = 3;
+  } else {
+    k = K;
+  }
+
+  // creating function to calculate the euclidean distance between 2 vectors
+  function euclideanDistance(x1, x2) {
+    // checking errors
+    if (x1.length !== x2.length) {
+      throw new Error('inconsistency between data and classification vector.');
+    }
+    // calculate the euclidean distance between 2 vectors and return
+    let totalSSE = 0;
+    for (let j = 0; j < x1.length; j += 1) {
+      totalSSE += (x1[j] - x2[j]) ** 2;
+    }
+    return Number(Math.sqrt(totalSSE).toFixed(2));
+  }
+
+  // starting algorithm
+
+  // calculate distance from toClassify to each point for all dimensions in dataX
+  // store distance and point's class_index into distance_class_list
+  let distanceList = [];
+  for (let i = 0; i < dataX.length; i += 1) {
+    const tmStore = [];
+    tmStore.push(euclideanDistance(dataX[i], toClassify));
+    tmStore.push(dataY[i]);
+    distanceList[i] = tmStore;
+  }
+
+  // sort distanceList
+  // take initial k values, count with class index
+  distanceList = distanceList.sort().slice(0, k);
+
+  // count the number of instances of each class in top k members
+  // with that maintain record of highest count class simultanously
+  const modeK = {};
+  const maxm = [-1, -1];
+  for (let i = 0; i < Math.min(k, distanceList.length); i += 1) {
+    if (distanceList[i][1] in modeK) modeK[distanceList[i][1]] += 1;
+    else modeK[distanceList[i][1]] = 1;
+    if (modeK[distanceList[i][1]] > maxm[0]) {
+      [maxm[0], maxm[1]] = [modeK[distanceList[i][1]], distanceList[i][1]];
+    }
+  }
+  // return the class with highest count from maxm
+  return maxm[1];
+}