hxx/javascript-algorithms
1
0
Fork 0
mirror of https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git synced 2024-12-25 22:46:20 +08:00
Code Issues Packages Projects Releases Wiki Activity

Update Fourier README.

Browse Source
This commit is contained in:
Oleksii Trekhleb 2018-08-14 23:03:07 +03:00
parent 1fb9d78751
commit 8e66189eff
1 changed files with 82 additions and 4 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

86
src/algorithms/math/fast-fourier-transform/README.md
View File

@ -1,11 +1,89 @@
# Discrete Fourier transform
The Discrete Fourier transform transforms a sequence of `N` complex numbers
**{x<sub>n</sub>}** := **x<sub>0</sub>, x<sub>1</sub>, x<sub>2</sub> ..., x<sub>N-1</sub>** &nbsp;&nbsp;into another sequence of complex numbers <br> **{X<sub>k</sub>}** := **X<sub>0</sub>, X<sub>1</sub>, X<sub>2</sub> ..., X<sub>N-1</sub>**&nbsp;&nbsp;&nbsp; which is defined by
# Fourier Transform
![alt text](https://wikimedia.org/api/rest_v1/media/math/render/svg/1af0a78dc50bbf118ab6bd4c4dcc3c4ff8502223)
## Definitions
The **Fourier Transform** (**FT**) decomposes a function of time (a signal) into
the frequencies that make it up, in a way similar to how a musical chord can be
expressed as the frequencies (or pitches) of its constituent notes.
The **Discrete Fourier Transform** (**DFT**) converts a finite sequence of
equally-spaced samples of a function into a same-length sequence of
equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a
complex-valued function of frequency. The interval at which the DTFT is sampled
is the reciprocal of the duration of the input sequence. An inverse DFT is a
Fourier series, using the DTFT samples as coefficients of complex sinusoids at
the corresponding DTFT frequencies. It has the same sample-values as the original
input sequence. The DFT is therefore said to be a frequency domain representation
of the original input sequence. If the original sequence spans all the non-zero
values of a function, its DTFT is continuous (and periodic), and the DFT provides
discrete samples of one cycle. If the original sequence is one cycle of a periodic
function, the DFT provides all the non-zero values of one DTFT cycle.
The Discrete Fourier transform transforms a sequence of `N` complex numbers:
{x<sub>n</sub>} = x<sub>0</sub>, x<sub>1</sub>, x<sub>2</sub> ..., x<sub>N-1</sub>
into another sequence of complex numbers:
{X<sub>k</sub>} = X<sub>0</sub>, X<sub>1</sub>, X<sub>2</sub> ..., X<sub>N-1</sub>
which is defined by:
![DFT](https://wikimedia.org/api/rest_v1/media/math/render/svg/1af0a78dc50bbf118ab6bd4c4dcc3c4ff8502223)
The **Discrete-Time Fourier Transform** (**DTFT**) is a form of Fourier analysis
that is applicable to the uniformly-spaced samples of a continuous function. The
term discrete-time refers to the fact that the transform operates on discrete data
(samples) whose interval often has units of time. From only the samples, it
produces a function of frequency that is a periodic summation of the continuous
Fourier transform of the original continuous function.
A **Fast Fourier Transform** (**FFT**) is an algorithm that samples a signal over
a period of time (or space) and divides it into its frequency components. These
components are single sinusoidal oscillations at distinct frequencies each with
their own amplitude and phase.
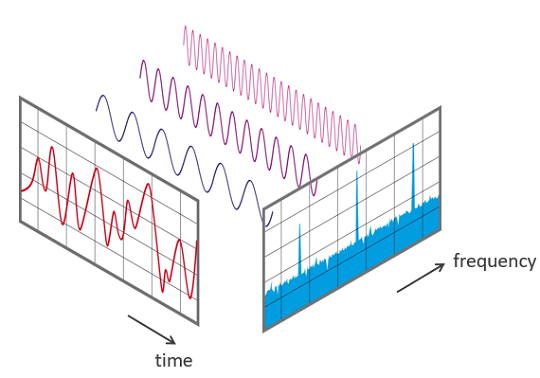
This transformation is illustrated in Diagram below. Over the time period measured
in the diagram, the signal contains 3 distinct dominant frequencies.
View of a signal in the time and frequency domain:
![FFT](https://upload.wikimedia.org/wikipedia/commons/6/61/FFT-Time-Frequency-View.png)
An FFT algorithm computes the discrete Fourier transform (DFT) of a sequence, or
its inverse (IFFT). Fourier analysis converts a signal from its original domain
to a representation in the frequency domain and vice versa. An FFT rapidly
computes such transformations by factorizing the DFT matrix into a product of
sparse (mostly zero) factors. As a result, it manages to reduce the complexity of
computing the DFT from O(n<sup>2</sup>), which arises if one simply applies the
definition of DFT, to O(n log n), where n is the data size.
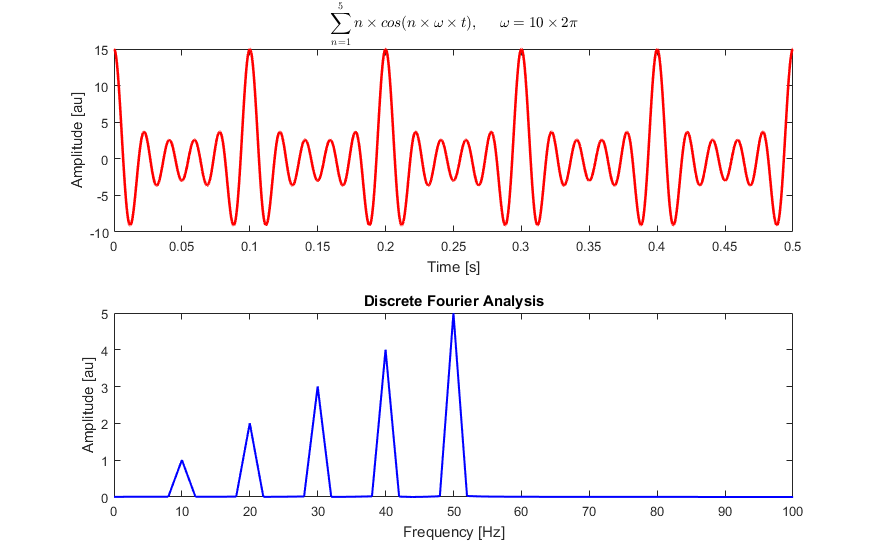
Here a discrete Fourier analysis of a sum of cosine waves at 10, 20, 30, 40,
and 50 Hz:
![FFT](https://upload.wikimedia.org/wikipedia/commons/6/64/FFT_of_Cosine_Summation_Function.png)
## Explanation
The Fourier Transform is one of deepest insights ever made. Unfortunately, the
meaning is buried within dense equations:
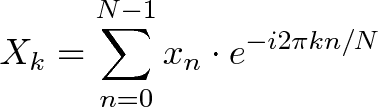
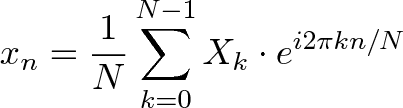
![](https://betterexplained.com/wp-content/plugins/wp-latexrender/pictures/45c088dbb767150fc0bacfeb49dd49e5.png)
![](https://betterexplained.com/wp-content/plugins/wp-latexrender/pictures/faeb9c5bf2e60add63ae4a70b293c7b4.png)
Rather than jumping into the symbols, let's experience the key idea firsthand. Here's a plain-English metaphor:
- *What does the Fourier Transform do?* Given a smoothie, it finds the recipe.
- *How?* Run the smoothie through filters to extract each ingredient.
- *Why?* Recipes are easier to analyze, compare, and modify than the smoothie itself.
- *How do we get the smoothie back?* Blend the ingredients.
## References
- [An Interactive Guide To The Fourier Transform](https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/)
- [YouTube by Better Explained](https://www.youtube.com/watch?v=iN0VG9N2q0U&t=0s&index=77&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
- [YouTube by 3Blue1Brown](https://www.youtube.com/watch?v=spUNpyF58BY&t=0s&index=76&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
- [Wikipedia, FT](https://en.wikipedia.org/wiki/Fourier_transform)
- [Wikipedia, DFT](https://www.wikiwand.com/en/Discrete_Fourier_transform)
- [Wikipedia, DTFT](https://en.wikipedia.org/wiki/Discrete-time_Fourier_transform)
- [Wikipedia, FFT](https://www.wikiwand.com/en/Fast_Fourier_transform)