mirror of
https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git
synced 2024-11-10 11:09:43 +08:00
Add Jump Search algorithm.
This commit is contained in:
parent
b73ddec94d
commit
a327b68a06
@ -84,6 +84,7 @@ a set of rules that precisely define a sequence of operations.
|
||||
* `A` [Regular Expression Matching](src/algorithms/string/regular-expression-matching)
|
||||
* **Searches**
|
||||
* `B` [Linear Search](src/algorithms/search/linear-search)
|
||||
* `B` [Jump Search](src/algorithms/search/jump-search)
|
||||
* `B` [Binary Search](src/algorithms/search/binary-search)
|
||||
* **Sorting**
|
||||
* `B` [Bubble Sort](src/algorithms/sorting/bubble-sort)
|
||||
@ -129,6 +130,7 @@ of algorithms. It is an abstraction higher than the notion of an algorithm, just
|
||||
algorithm is an abstraction higher than a computer program.
|
||||
|
||||
* **Brute Force** - look at all the possibilities and selects the best solution
|
||||
* `B` [Linear Search](src/algorithms/search/linear-search)
|
||||
* `A` [Maximum Subarray](src/algorithms/sets/maximum-subarray)
|
||||
* `A` [Travelling Salesman Problem](src/algorithms/graph/travelling-salesman) - shortest possible route that visits each city and returns to the origin city
|
||||
* **Greedy** - choose the best option at the current time, without any consideration for the future
|
||||
|
||||
@ -12,6 +12,11 @@ in the array.
|
||||
|
||||

|
||||
|
||||
## Complexity
|
||||
|
||||
**Time Complexity**: `O(log(n))` - since we split search area by two for every
|
||||
next iteration.
|
||||
|
||||
## References
|
||||
|
||||
- [Wikipedia](https://en.wikipedia.org/wiki/Binary_search_algorithm)
|
||||
|
||||
@ -1,6 +1,8 @@
|
||||
import Comparator from '../../../utils/comparator/Comparator';
|
||||
|
||||
/**
|
||||
* Binary search implementation.
|
||||
*
|
||||
* @param {*[]} sortedArray
|
||||
* @param {*} seekElement
|
||||
* @param {function(a, b)} [comparatorCallback]
|
||||
|
||||
27
src/algorithms/search/jump-search/README.md
Normal file
27
src/algorithms/search/jump-search/README.md
Normal file
@ -0,0 +1,27 @@
|
||||
# Jump Search
|
||||
|
||||
Like Binary Search, **Jump Search** (or **Block Search**) is a searching algorithm
|
||||
for sorted arrays. The basic idea is to check fewer elements (than linear search)
|
||||
by jumping ahead by fixed steps or skipping some elements in place of searching all
|
||||
elements.
|
||||
|
||||
For example, suppose we have an array `arr[]` of size `n` and block (to be jumped)
|
||||
of size `m`. Then we search at the indexes `arr[0]`, `arr[m]`, `arr[2 * m]`, ..., `arr[k * m]` and
|
||||
so on. Once we find the interval `arr[k * m] < x < arr[(k+1) * m]`, we perform a
|
||||
linear search operation from the index `k * m` to find the element `x`.
|
||||
|
||||
**What is the optimal block size to be skipped?**
|
||||
In the worst case, we have to do `n/m` jumps and if the last checked value is
|
||||
greater than the element to be searched for, we perform `m - 1` comparisons more
|
||||
for linear search. Therefore the total number of comparisons in the worst case
|
||||
will be `((n/m) + m - 1)`. The value of the function `((n/m) + m - 1)` will be
|
||||
minimum when `m = √n`. Therefore, the best step size is `m = √n`.
|
||||
|
||||
## Complexity
|
||||
|
||||
**Time complexity**: `O(√n)` - because we do search by blocks of size `√n`.
|
||||
|
||||
## References
|
||||
|
||||
- [Wikipedia](https://en.wikipedia.org/wiki/Jump_search)
|
||||
- [GeeksForGeeks](https://www.geeksforgeeks.org/jump-search/)
|
||||
@ -0,0 +1,20 @@
|
||||
import jumpSearch from '../jumpSearch';
|
||||
|
||||
describe('jumpSearch', () => {
|
||||
it('should search for an element in sorted array', () => {
|
||||
expect(jumpSearch([], 1)).toBe(-1);
|
||||
expect(jumpSearch([1], 2)).toBe(-1);
|
||||
expect(jumpSearch([1], 1)).toBe(0);
|
||||
expect(jumpSearch([1, 2], 1)).toBe(0);
|
||||
expect(jumpSearch([1, 2], 1)).toBe(0);
|
||||
expect(jumpSearch([1, 1, 1], 1)).toBe(0);
|
||||
expect(jumpSearch([1, 2, 5, 10, 20, 21, 24, 30, 48], 2)).toBe(1);
|
||||
expect(jumpSearch([1, 2, 5, 10, 20, 21, 24, 30, 48], 0)).toBe(-1);
|
||||
expect(jumpSearch([1, 2, 5, 10, 20, 21, 24, 30, 48], 0)).toBe(-1);
|
||||
expect(jumpSearch([1, 2, 5, 10, 20, 21, 24, 30, 48], 7)).toBe(-1);
|
||||
expect(jumpSearch([1, 2, 5, 10, 20, 21, 24, 30, 48], 5)).toBe(2);
|
||||
expect(jumpSearch([1, 2, 5, 10, 20, 21, 24, 30, 48], 20)).toBe(4);
|
||||
expect(jumpSearch([1, 2, 5, 10, 20, 21, 24, 30, 48], 30)).toBe(7);
|
||||
expect(jumpSearch([1, 2, 5, 10, 20, 21, 24, 30, 48], 48)).toBe(8);
|
||||
});
|
||||
});
|
||||
51
src/algorithms/search/jump-search/jumpSearch.js
Normal file
51
src/algorithms/search/jump-search/jumpSearch.js
Normal file
@ -0,0 +1,51 @@
|
||||
import Comparator from '../../../utils/comparator/Comparator';
|
||||
|
||||
/**
|
||||
* Jump (block) search implementation.
|
||||
*
|
||||
* @param {*[]} sortedArray.
|
||||
* @param {*} seekElement
|
||||
* @param {function(a, b)} [comparatorCallback]
|
||||
* @return {number}
|
||||
*/
|
||||
export default function jumpSearch(sortedArray, seekElement, comparatorCallback) {
|
||||
const comparator = new Comparator(comparatorCallback);
|
||||
const arraySize = sortedArray.length;
|
||||
|
||||
if (!arraySize) {
|
||||
// We can't find anything in empty array.
|
||||
return -1;
|
||||
}
|
||||
|
||||
// Calculate optimal jump size.
|
||||
// Total number of comparisons in the worst case will be ((arraySize/jumpSize) + jumpSize - 1).
|
||||
// The value of the function ((arraySize/jumpSize) + jumpSize - 1) will be minimum
|
||||
// when jumpSize = √array.length.
|
||||
const jumpSize = Math.floor(Math.sqrt(arraySize));
|
||||
|
||||
// Find the block where the seekElement belong to.
|
||||
let blockStart = 0;
|
||||
let blockEnd = jumpSize;
|
||||
while (comparator.greaterThan(seekElement, sortedArray[Math.min(blockEnd, arraySize) - 1])) {
|
||||
// Jump to the next block.
|
||||
blockStart = blockEnd;
|
||||
blockEnd += jumpSize;
|
||||
|
||||
// If our next block is out of array then we couldn't found the element.
|
||||
if (blockStart > arraySize) {
|
||||
return -1;
|
||||
}
|
||||
}
|
||||
|
||||
// Do linear search for seekElement in subarray starting from blockStart.
|
||||
let currentIndex = blockStart;
|
||||
while (currentIndex < Math.min(blockEnd, arraySize)) {
|
||||
if (comparator.equal(sortedArray[currentIndex], seekElement)) {
|
||||
return currentIndex;
|
||||
}
|
||||
|
||||
currentIndex += 1;
|
||||
}
|
||||
|
||||
return -1;
|
||||
}
|
||||
@ -8,6 +8,11 @@ comparisons, where `n` is the length of the list.
|
||||
|
||||
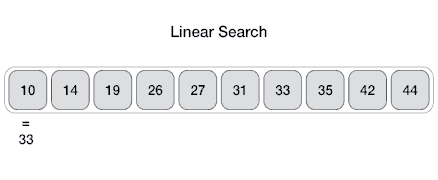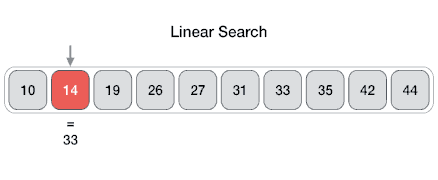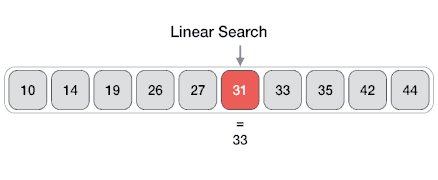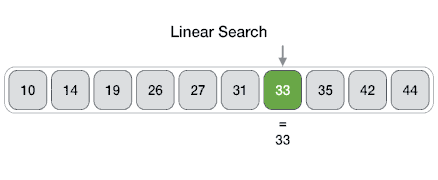
|
||||
|
||||
## Complexity
|
||||
|
||||
**Time Complexity**: `O(n)` - since in worst case we're checking each element
|
||||
exactly once.
|
||||
|
||||
## References
|
||||
- [Wikipedia](https://en.wikipedia.org/wiki/Linear_search)
|
||||
- [TutorialsPoint](https://www.tutorialspoint.com/data_structures_algorithms/linear_search_algorithm.htm)
|
||||
|
||||
@ -1,6 +1,8 @@
|
||||
import Comparator from '../../../utils/comparator/Comparator';
|
||||
|
||||
/**
|
||||
* Linear search implementation.
|
||||
*
|
||||
* @param {*[]} array
|
||||
* @param {*} seekElement
|
||||
* @param {function(a, b)} [comparatorCallback]
|
||||
|
||||
Loading…
Reference in New Issue
Block a user