Merge branch 'master' into master

.github/workflows/node.js.yml

@@ -0,0 +1,37 @@
+name: CI
+
+on:
+  push:
+    branches: [ master ]
+  pull_request:
+    branches: [ master ]
+
+jobs:
+  build:
+
+    runs-on: ubuntu-latest
+
+    strategy:
+      matrix:
+        node-version: [14.x]
+
+    steps:
+    - name: Checkout repository
+      uses: actions/checkout@v2
+
+    - name: Setup Node.js ${{ matrix.node-version }}
+      uses: actions/setup-node@v1
+      with:
+        node-version: ${{ matrix.node-version }}
+
+    - name: Install dependencies
+      run: npm i
+
+    - name: Run linting
+      run: npm run lint
+
+    - name: Run tests
+      run: npm run coverage
+
+    - name: Upload coverage to Codecov
+      uses: codecov/codecov-action@v1

.travis.yml

@@ -1,15 +0,0 @@
-os:
-  - linux
-  - osx
-dist: trusty
-language: node_js
-node_js:
-  - "12"
-install:
-  - npm install -g codecov
-  - npm install
-script:
-  - npm run ci
-  - codecov
-notifications:
-  email: false

BACKERS.md

@@ -1,3 +1,27 @@
-# Sponsors & Backers
+# Project Backers
+
+> You may support this project via ❤️️ [GitHub](https://github.com/sponsors/trekhleb) or ❤️️ [Patreon](https://www.patreon.com/trekhleb).  
+
+## `O(2ⁿ)` Backers
+
+⏳
+
+## `O(n²)` Backers
+
+⏳
+
+## `O(n×log(n))` Backers
+
+<ul>
+  <li>
+    <a href="https://github.com/bullwinkle">
+      <img
+        src="https://avatars1.githubusercontent.com/u/3613558?s=60&amp;v=4"
+        width="30"
+        height="30"
+      /></a>
+    &thinsp;
+    <a href="https://github.com/bullwinkle">bullwinkle</a>
+  </li>
+</ul>
 
-Work on this document is in progress...

README.es-ES.md

@@ -1,6 +1,6 @@
 # Algoritmos y Estructuras de Datos en JavaScript
 
-[![Build Status](https://travis-ci.org/trekhleb/javascript-algorithms.svg?branch=master)](https://travis-ci.org/trekhleb/javascript-algorithms)
+[![CI](https://github.com/trekhleb/javascript-algorithms/workflows/CI/badge.svg)](https://github.com/trekhleb/javascript-algorithms/actions)
 [![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)
 
 Este repositorio contiene ejemplos basados en JavaScript de muchos
@@ -17,7 +17,10 @@ _Léelo en otros idiomas:_
 [_日本語_](README.ja-JP.md),
 [_Polski_](README.pl-PL.md),
 [_Français_](README.fr-FR.md),
-[_Português_](README.pt-BR.md)
+[_Português_](README.pt-BR.md),
+[_Русский_](README.ru-RU.md),
+[_Türk_](README.tr-TR.md),
+[_Italiana_](README.it-IT.md)
 
 *☝ Nótese que este proyecto está pensado con fines de aprendizaje e investigación,
 y **no** para ser usado en producción.*

README.fr-FR.md

@@ -1,13 +1,13 @@
 # Algorithmes et Structures de Données en JavaScript
 
-[![Build Status](https://travis-ci.org/trekhleb/javascript-algorithms.svg?branch=master)](https://travis-ci.org/trekhleb/javascript-algorithms)
+[![CI](https://github.com/trekhleb/javascript-algorithms/workflows/CI/badge.svg)](https://github.com/trekhleb/javascript-algorithms/actions)
 [![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)
 
-Ce dépôt contient des exemples d'implémentation en JavaScript de plusieurs 
+Ce dépôt contient des exemples d'implémentation en JavaScript de plusieurs
 algorithmes et structures de données populaires.
 
-Chaque algorithme et structure de donnée possède son propre README contenant 
-les explications détaillées et liens (incluant aussi des vidéos Youtube) pour 
+Chaque algorithme et structure de donnée possède son propre README contenant
+les explications détaillées et liens (incluant aussi des vidéos Youtube) pour
 complément d'informations.
 
 _Lisez ceci dans d'autres langues:_
@@ -18,178 +18,185 @@ _Lisez ceci dans d'autres langues:_
 [_日本語_](README.ja-JP.md),
 [_Polski_](README.pl-PL.md),
 [_Español_](README.es-ES.md),
-[_Português_](README.pt-BR.md)
+[_Português_](README.pt-BR.md),
+[_Русский_](README.ru-RU.md),
+[_Türk_](README.tr-TR.md),
+[_Italiana_](README.it-IT.md)
 
 ## Data Structures
 
-Une structure de données est une manière spéciale d'organiser et de stocker 
-des données dans un ordinateur de manière à ce que l'on puisse accéder à 
-cette information et la modifier de manière efficiente. De manière plus 
-spécifique, une structure de données est un ensemble composé d'une collection 
-de valeurs, des relations entre ces valeurs ainsi que d'un ensemble de 
+Une structure de données est une manière spéciale d'organiser et de stocker
+des données dans un ordinateur de manière à ce que l'on puisse accéder à
+cette information et la modifier de manière efficiente. De manière plus
+spécifique, une structure de données est un ensemble composé d'une collection
+de valeurs, des relations entre ces valeurs ainsi que d'un ensemble de
 fonctions ou d'opérations pouvant être appliquées sur ces données.
 
 `B` - Débutant, `A` - Avancé
 
-* `B` [Liste Chaînée](src/data-structures/linked-list)
-* `B` [Liste Doublement Chaînée](src/data-structures/doubly-linked-list)
-* `B` [Queue](src/data-structures/queue)
-* `B` [Pile](src/data-structures/stack)
-* `B` [Table de Hachage](src/data-structures/hash-table)
-* `B` [Tas](src/data-structures/heap)
-* `B` [Queue de Priorité](src/data-structures/priority-queue)
-* `A` [Trie](src/data-structures/trie)
-* `A` [Arbre](src/data-structures/tree)
-  * `A` [Arbre de recherche Binaire](src/data-structures/tree/binary-search-tree)
-  * `A` [Arbre AVL](src/data-structures/tree/avl-tree)
-  * `A` [Arbre Red-Black](src/data-structures/tree/red-black-tree)
-  * `A` [Arbre de Segments](src/data-structures/tree/segment-tree) - avec exemples de requêtes de type min/max/somme sur intervalles
-  * `A` [Arbre de Fenwick](src/data-structures/tree/fenwick-tree) (Arbre Binaire Indexé)
-* `A` [Graphe](src/data-structures/graph) (orienté et non orienté)
-* `A` [Ensembles Disjoints](src/data-structures/disjoint-set)
-* `A` [Filtre de Bloom](src/data-structures/bloom-filter)
+- `B` [Liste Chaînée](src/data-structures/linked-list)
+- `B` [Liste Doublement Chaînée](src/data-structures/doubly-linked-list)
+- `B` [Queue](src/data-structures/queue)
+- `B` [Pile](src/data-structures/stack)
+- `B` [Table de Hachage](src/data-structures/hash-table)
+- `B` [Tas](src/data-structures/heap)
+- `B` [Queue de Priorité](src/data-structures/priority-queue)
+- `A` [Trie](src/data-structures/trie)
+- `A` [Arbre](src/data-structures/tree)
+  - `A` [Arbre de recherche Binaire](src/data-structures/tree/binary-search-tree)
+  - `A` [Arbre AVL](src/data-structures/tree/avl-tree)
+  - `A` [Arbre Red-Black](src/data-structures/tree/red-black-tree)
+  - `A` [Arbre de Segments](src/data-structures/tree/segment-tree) - avec exemples de requêtes de type min/max/somme sur intervalles
+  - `A` [Arbre de Fenwick](src/data-structures/tree/fenwick-tree) (Arbre Binaire Indexé)
+- `A` [Graphe](src/data-structures/graph) (orienté et non orienté)
+- `A` [Ensembles Disjoints](src/data-structures/disjoint-set)
+- `A` [Filtre de Bloom](src/data-structures/bloom-filter)
 
 ## Algorithmes
 
-Un algorithme est une démarche non ambigüe expliquant comment résoudre une 
-classe de problèmes. C'est un ensemble de règles décrivant de manière précise 
+Un algorithme est une démarche non ambigüe expliquant comment résoudre une
+classe de problèmes. C'est un ensemble de règles décrivant de manière précise
 une séquence d'opérations.
 
 `B` - Débutant, `A` - Avancé
 
 ### Algorithmes par topic
 
-* **Math**
-  * `B` [Manipulation de Bit](src/algorithms/math/bits) - définir/obtenir/mettre à jour/effacer les bits, multiplication/division par deux, négativiser etc.
-  * `B` [Factorielle](src/algorithms/math/factorial) 
-  * `B` [Nombre de Fibonacci](src/algorithms/math/fibonacci)
-  * `B` [Test de Primalité](src/algorithms/math/primality-test) (méthode du test de division)
-  * `B` [Algorithme d'Euclide](src/algorithms/math/euclidean-algorithm) - calcule le Plus Grand Commun Diviseur (PGCD)
-  * `B` [Plus Petit Commun Multiple](src/algorithms/math/least-common-multiple) (PPCM)
-  * `B` [Crible d'Eratosthène](src/algorithms/math/sieve-of-eratosthenes) - trouve tous les nombres premiers inférieurs à une certaine limite
-  * `B` [Puissance de Deux](src/algorithms/math/is-power-of-two) - teste si un nombre donné est une puissance de deux (algorithmes naif et basé sur les opérations bit-à-bit)
-  * `B` [Triangle de Pascal](src/algorithms/math/pascal-triangle)
-  * `A` [Partition Entière](src/algorithms/math/integer-partition)
-  * `A` [Approximation de π par l'algorithme de Liu Hui](src/algorithms/math/liu-hui) - approximation du calcul de π basé sur les N-gons
-* **Ensembles**
-  * `B` [Produit Cartésien](src/algorithms/sets/cartesian-product) - produit de plusieurs ensembles
-  * `B` [Mélange de Fisher–Yates](src/algorithms/sets/fisher-yates) - permulation aléatoire d'une séquence finie
-  * `A` [Ensemble des parties d'un ensemble](src/algorithms/sets/power-set) - tous les sous-ensembles d'un ensemble
-  * `A` [Permutations](src/algorithms/sets/permutations) (avec et sans répétitions)
-  * `A` [Combinaisons](src/algorithms/sets/combinations) (avec et sans répétitions)
-  * `A` [Plus Longue Sous-séquence Commune](src/algorithms/sets/longest-common-subsequence)
-  * `A` [Plus Longue Sous-suite strictement croissante](src/algorithms/sets/longest-increasing-subsequence)
-  * `A` [Plus Courte Super-séquence Commune](src/algorithms/sets/shortest-common-supersequence)
-  * `A` [Problème du Sac à Dos](src/algorithms/sets/knapsack-problem) - versions "0/1" et "Sans Contraintes"
-  * `A` [Sous-partie Maximum](src/algorithms/sets/maximum-subarray) - versions "Force Brute" et "Programmation Dynamique" (Kadane)
-  * `A` [Somme combinatoire](src/algorithms/sets/combination-sum) - trouve toutes les combinaisons qui forment une somme spécifique
-* **Chaînes de Caractères**
-  * `B` [Distance de Hamming](src/algorithms/string/hamming-distance) - nombre de positions auxquelles les symboles sont différents
-  * `A` [Distance de Levenshtein](src/algorithms/string/levenshtein-distance) - distance minimale d'édition entre deux séquences
-  * `A` [Algorithme de Knuth–Morris–Pratt](src/algorithms/string/knuth-morris-pratt) (Algorithme KMP) - recherche de sous-chaîne (pattern matching)
-  * `A` [Algorithme Z](src/algorithms/string/z-algorithm) - recherche de sous-chaîne (pattern matching)
-  * `A` [Algorithme de Rabin Karp](src/algorithms/string/rabin-karp) - recherche de sous-chaîne
-  * `A` [Plus Longue Sous-chaîne Commune](src/algorithms/string/longest-common-substring)
-  * `A` [Expression Régulière](src/algorithms/string/regular-expression-matching)
-* **Recherche**
-  * `B` [Recherche Linéaire](src/algorithms/search/linear-search)
-  * `B` [Jump Search](src/algorithms/search/jump-search) Recherche par saut (ou par bloc) - recherche dans une liste triée
-  * `B` [Recherche Binaire](src/algorithms/search/binary-search) - recherche dans une liste triée
-  * `B` [Recherche par Interpolation](src/algorithms/search/interpolation-search) - recherche dans une liste triée et uniformément distribuée
-* **Tri**
-  * `B` [Tri Bullet](src/algorithms/sorting/bubble-sort)
-  * `B` [Tri Sélection](src/algorithms/sorting/selection-sort)
-  * `B` [Tri Insertion](src/algorithms/sorting/insertion-sort)
-  * `B` [Tri Par Tas](src/algorithms/sorting/heap-sort)
-  * `B` [Tri Fusion](src/algorithms/sorting/merge-sort)
-  * `B` [Tri Rapide](src/algorithms/sorting/quick-sort) - implémentations *in-place* et *non in-place*
-  * `B` [Tri Shell](src/algorithms/sorting/shell-sort)
-  * `B` [Tri Comptage](src/algorithms/sorting/counting-sort)
-  * `B` [Tri Radix](src/algorithms/sorting/radix-sort)
-* **Arbres**
-  * `B` [Parcours en Profondeur](src/algorithms/tree/depth-first-search) (DFS)
-  * `B` [Parcours en Largeur](src/algorithms/tree/breadth-first-search) (BFS)
-* **Graphes**
-  * `B` [Parcours en Profondeur](src/algorithms/graph/depth-first-search) (DFS)
-  * `B` [Parcours en Largeur](src/algorithms/graph/breadth-first-search) (BFS)
-  * `B` [Algorithme de Kruskal](src/algorithms/graph/kruskal) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
-  * `A` [Algorithme de Dijkstra](src/algorithms/graph/dijkstra) - trouver tous les plus courts chemins  partant d'un noeud vers tous les autres noeuds dans un graphe
-  * `A` [Algorithme de Bellman-Ford](src/algorithms/graph/bellman-ford) - trouver tous les plus courts chemins  partant d'un noeud vers tous les autres noeuds dans un graphe
-  * `A` [Algorithme de Floyd-Warshall](src/algorithms/graph/floyd-warshall) - trouver tous les plus courts chemins  entre toutes les paires de noeuds dans un graphe
-  * `A` [Détection de Cycle](src/algorithms/graph/detect-cycle) - pour les graphes dirigés et non dirigés (implémentations basées sur l'algorithme de Parcours en Profondeur et sur les Ensembles Disjoints)
-  * `A` [Algorithme de Prim](src/algorithms/graph/prim) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
-  * `A` [Tri Topologique](src/algorithms/graph/topological-sorting) - méthode DFS
-  * `A` [Point d'Articulation](src/algorithms/graph/articulation-points) - algorithme de Tarjan (basé sur l'algorithme de Parcours en Profondeur)
-  * `A` [Bridges](src/algorithms/graph/bridges) - algorithme basé sur le Parcours en Profondeur
-  * `A` [Chemin Eulérien et Circuit Eulérien](src/algorithms/graph/eulerian-path) - algorithme de Fleury - visite chaque arc exactement une fois
-  * `A` [Cycle Hamiltonien](src/algorithms/graph/hamiltonian-cycle) - visite chaque noeud exactement une fois
-  * `A` [Composants Fortements Connexes](src/algorithms/graph/strongly-connected-components) - algorithme de Kosaraju
-  * `A` [Problème du Voyageur de Commerce](src/algorithms/graph/travelling-salesman) - chemin le plus court visitant chaque cité et retournant à la cité d'origine
-* **Non catégorisé**
-  * `B` [Tours de Hanoi](src/algorithms/uncategorized/hanoi-tower)
-  * `B` [Rotation de Matrice Carrée](src/algorithms/uncategorized/square-matrix-rotation) - algorithme *in place*
-  * `B` [Jump Game](src/algorithms/uncategorized/jump-game) - retour sur trace, programmation dynamique (haut-bas + bas-haut) et exemples gourmands 
-  * `B` [Chemins Uniques](src/algorithms/uncategorized/unique-paths) - retour sur trace, programmation dynamique (haut-bas + bas-haut) et exemples basés sur le Triangle de Pascal 
-  * `A` [Problème des N-Dames](src/algorithms/uncategorized/n-queens)
-  * `A` [Problème du Cavalier](src/algorithms/uncategorized/knight-tour)
+- **Math**
+  - `B` [Manipulation de Bit](src/algorithms/math/bits/README.fr-FR.md) - définir/obtenir/mettre à jour/effacer les bits, multiplication/division par deux, négativiser etc.
+  - `B` [Factorielle](src/algorithms/math/factorial/README.fr-FR.md)
+  - `B` [Nombre de Fibonacci](src/algorithms/math/fibonacci/README.fr-FR.md)
+  - `B` [Test de Primalité](src/algorithms/math/primality-test) (méthode du test de division)
+  - `B` [Algorithme d'Euclide](src/algorithms/math/euclidean-algorithm/README.fr-FR.md) - calcule le Plus Grand Commun Diviseur (PGCD)
+  - `B` [Plus Petit Commun Multiple](src/algorithms/math/least-common-multiple) (PPCM)
+  - `B` [Crible d'Eratosthène](src/algorithms/math/sieve-of-eratosthenes) - trouve tous les nombres premiers inférieurs à une certaine limite
+  - `B` [Puissance de Deux](src/algorithms/math/is-power-of-two) - teste si un nombre donné est une puissance de deux (algorithmes naif et basé sur les opérations bit-à-bit)
+  - `B` [Triangle de Pascal](src/algorithms/math/pascal-triangle)
+  - `B` [Nombre complexe](src/algorithms/math/complex-number/README.fr-FR.md) - nombres complexes et opérations de bases
+  - `A` [Partition Entière](src/algorithms/math/integer-partition)
+  - `A` [Approximation de π par l'algorithme de Liu Hui](src/algorithms/math/liu-hui) - approximation du calcul de π basé sur les N-gons
+  - `B` [Exponentiation rapide](src/algorithms/math/fast-powering/README.fr-FR.md)
+  - `A` [Transformée de Fourier Discrète](src/algorithms/math/fourier-transform/README.fr-FR.md) - décomposer une fonction du temps (un signal) en fréquences qui la composent
+- **Ensembles**
+  - `B` [Produit Cartésien](src/algorithms/sets/cartesian-product) - produit de plusieurs ensembles
+  - `B` [Mélange de Fisher–Yates](src/algorithms/sets/fisher-yates) - permulation aléatoire d'une séquence finie
+  - `A` [Ensemble des parties d'un ensemble](src/algorithms/sets/power-set) - tous les sous-ensembles d'un ensemble
+  - `A` [Permutations](src/algorithms/sets/permutations) (avec et sans répétitions)
+  - `A` [Combinaisons](src/algorithms/sets/combinations) (avec et sans répétitions)
+  - `A` [Plus Longue Sous-séquence Commune](src/algorithms/sets/longest-common-subsequence)
+  - `A` [Plus Longue Sous-suite strictement croissante](src/algorithms/sets/longest-increasing-subsequence)
+  - `A` [Plus Courte Super-séquence Commune](src/algorithms/sets/shortest-common-supersequence)
+  - `A` [Problème du Sac à Dos](src/algorithms/sets/knapsack-problem) - versions "0/1" et "Sans Contraintes"
+  - `A` [Sous-partie Maximum](src/algorithms/sets/maximum-subarray) - versions "Force Brute" et "Programmation Dynamique" (Kadane)
+  - `A` [Somme combinatoire](src/algorithms/sets/combination-sum) - trouve toutes les combinaisons qui forment une somme spécifique
+- **Chaînes de Caractères**
+  - `B` [Distance de Hamming](src/algorithms/string/hamming-distance) - nombre de positions auxquelles les symboles sont différents
+  - `A` [Distance de Levenshtein](src/algorithms/string/levenshtein-distance) - distance minimale d'édition entre deux séquences
+  - `A` [Algorithme de Knuth–Morris–Pratt](src/algorithms/string/knuth-morris-pratt) (Algorithme KMP) - recherche de sous-chaîne (pattern matching)
+  - `A` [Algorithme Z](src/algorithms/string/z-algorithm) - recherche de sous-chaîne (pattern matching)
+  - `A` [Algorithme de Rabin Karp](src/algorithms/string/rabin-karp) - recherche de sous-chaîne
+  - `A` [Plus Longue Sous-chaîne Commune](src/algorithms/string/longest-common-substring)
+  - `A` [Expression Régulière](src/algorithms/string/regular-expression-matching)
+- **Recherche**
+  - `B` [Recherche Linéaire](src/algorithms/search/linear-search)
+  - `B` [Jump Search](src/algorithms/search/jump-search) Recherche par saut (ou par bloc) - recherche dans une liste triée
+  - `B` [Recherche Binaire](src/algorithms/search/binary-search) - recherche dans une liste triée
+  - `B` [Recherche par Interpolation](src/algorithms/search/interpolation-search) - recherche dans une liste triée et uniformément distribuée
+- **Tri**
+  - `B` [Tri Bullet](src/algorithms/sorting/bubble-sort)
+  - `B` [Tri Sélection](src/algorithms/sorting/selection-sort)
+  - `B` [Tri Insertion](src/algorithms/sorting/insertion-sort)
+  - `B` [Tri Par Tas](src/algorithms/sorting/heap-sort)
+  - `B` [Tri Fusion](src/algorithms/sorting/merge-sort)
+  - `B` [Tri Rapide](src/algorithms/sorting/quick-sort) - implémentations _in-place_ et _non in-place_
+  - `B` [Tri Shell](src/algorithms/sorting/shell-sort)
+  - `B` [Tri Comptage](src/algorithms/sorting/counting-sort)
+  - `B` [Tri Radix](src/algorithms/sorting/radix-sort)
+- **Arbres**
+  - `B` [Parcours en Profondeur](src/algorithms/tree/depth-first-search) (DFS)
+  - `B` [Parcours en Largeur](src/algorithms/tree/breadth-first-search) (BFS)
+- **Graphes**
+  - `B` [Parcours en Profondeur](src/algorithms/graph/depth-first-search) (DFS)
+  - `B` [Parcours en Largeur](src/algorithms/graph/breadth-first-search) (BFS)
+  - `B` [Algorithme de Kruskal](src/algorithms/graph/kruskal) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
+  - `A` [Algorithme de Dijkstra](src/algorithms/graph/dijkstra) - trouver tous les plus courts chemins partant d'un noeud vers tous les autres noeuds dans un graphe
+  - `A` [Algorithme de Bellman-Ford](src/algorithms/graph/bellman-ford) - trouver tous les plus courts chemins partant d'un noeud vers tous les autres noeuds dans un graphe
+  - `A` [Algorithme de Floyd-Warshall](src/algorithms/graph/floyd-warshall) - trouver tous les plus courts chemins entre toutes les paires de noeuds dans un graphe
+  - `A` [Détection de Cycle](src/algorithms/graph/detect-cycle) - pour les graphes dirigés et non dirigés (implémentations basées sur l'algorithme de Parcours en Profondeur et sur les Ensembles Disjoints)
+  - `A` [Algorithme de Prim](src/algorithms/graph/prim) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
+  - `A` [Tri Topologique](src/algorithms/graph/topological-sorting) - méthode DFS
+  - `A` [Point d'Articulation](src/algorithms/graph/articulation-points) - algorithme de Tarjan (basé sur l'algorithme de Parcours en Profondeur)
+  - `A` [Bridges](src/algorithms/graph/bridges) - algorithme basé sur le Parcours en Profondeur
+  - `A` [Chemin Eulérien et Circuit Eulérien](src/algorithms/graph/eulerian-path) - algorithme de Fleury - visite chaque arc exactement une fois
+  - `A` [Cycle Hamiltonien](src/algorithms/graph/hamiltonian-cycle) - visite chaque noeud exactement une fois
+  - `A` [Composants Fortements Connexes](src/algorithms/graph/strongly-connected-components) - algorithme de Kosaraju
+  - `A` [Problème du Voyageur de Commerce](src/algorithms/graph/travelling-salesman) - chemin le plus court visitant chaque cité et retournant à la cité d'origine
+- **Non catégorisé**
+  - `B` [Tours de Hanoi](src/algorithms/uncategorized/hanoi-tower)
+  - `B` [Rotation de Matrice Carrée](src/algorithms/uncategorized/square-matrix-rotation) - algorithme _in place_
+  - `B` [Jump Game](src/algorithms/uncategorized/jump-game) - retour sur trace, programmation dynamique (haut-bas + bas-haut) et exemples gourmands
+  - `B` [Chemins Uniques](src/algorithms/uncategorized/unique-paths) - retour sur trace, programmation dynamique (haut-bas + bas-haut) et exemples basés sur le Triangle de Pascal
+  - `A` [Problème des N-Dames](src/algorithms/uncategorized/n-queens)
+  - `A` [Problème du Cavalier](src/algorithms/uncategorized/knight-tour)
 
 ### Algorithmes par Paradigme
 
-Un paradigme algorithmique est une méthode générique ou une approche qui 
-sous-tend la conception d'une classe d'algorithmes. C'est une abstraction 
-au-dessus de la notion d'algorithme, tout comme l'algorithme est une abstraction 
+Un paradigme algorithmique est une méthode générique ou une approche qui
+sous-tend la conception d'une classe d'algorithmes. C'est une abstraction
+au-dessus de la notion d'algorithme, tout comme l'algorithme est une abstraction
 supérieure à un programme informatique.
 
-* **Force Brute** - cherche parmi toutes les possibilités et retient la meilleure
-  * `B` [Recherche Linéaire](src/algorithms/search/linear-search)
-  * `A` [Sous-partie Maximum](src/algorithms/sets/maximum-subarray)
-  * `A` [Problème du Voyageur de Commerce](src/algorithms/graph/travelling-salesman) - chemin le plus court visitant chaque cité et retournant à la cité d'origine
-* **Gourmand** - choisit la meilleure option à l'instant courant, sans tenir compte de la situation future
-  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
-  * `A` [Problème du Sac à Dos Sans Contraintes](src/algorithms/sets/knapsack-problem)
-  * `A` [Algorithme de Dijkstra](src/algorithms/graph/dijkstra) - trouver tous les plus courts chemins  partant d'un noeud vers tous les autres noeuds dans un graphe
-  * `A` [Algorithme de Prim](src/algorithms/graph/prim) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
-  * `A` [Algorithme de Kruskal](src/algorithms/graph/kruskal) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
-* **Diviser et Régner** - divise le problème en sous problèmes (plus simples) et résoud ces sous problèmes
-  * `B` [Recherche Binaire](src/algorithms/search/binary-search)
-  * `B` [Tours de Hanoi](src/algorithms/uncategorized/hanoi-tower)
-  * `B` [Triangle de Pascal](src/algorithms/math/pascal-triangle)
-  * `B` [Algorithme d'Euclide](src/algorithms/math/euclidean-algorithm) - calcule le Plus Grand Commun Diviseur (PGCD)
-  * `B` [Tri Fusion](src/algorithms/sorting/merge-sort)
-  * `B` [Tri Rapide](src/algorithms/sorting/quick-sort)
-  * `B` [Arbre de Parcours en Profondeur](src/algorithms/tree/depth-first-search) (DFS)
-  * `B` [Graphe de Parcours en Profondeur](src/algorithms/graph/depth-first-search) (DFS)
-  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
-  * `A` [Permutations](src/algorithms/sets/permutations) (avec et sans répétitions)
-  * `A` [Combinations](src/algorithms/sets/combinations) (avec et sans répétitions)
-* **Programmation Dynamique** - construit une solution en utilisant les solutions précédemment trouvées
-  * `B` [Nombre de Fibonacci](src/algorithms/math/fibonacci)
-  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
-  * `B` [Chemins Uniques](src/algorithms/uncategorized/unique-paths)
-  * `A` [Distance de Levenshtein](src/algorithms/string/levenshtein-distance) - distance minimale d'édition entre deux séquences
-  * `A` [Plus Longue Sous-séquence Commune](src/algorithms/sets/longest-common-subsequence)
-  * `A` [Plus Longue Sous-chaîne Commune](src/algorithms/string/longest-common-substring)
-  * `A` [Plus Longue Sous-suite strictement croissante](src/algorithms/sets/longest-increasing-subsequence)
-  * `A` [Plus Courte Super-séquence Commune](src/algorithms/sets/shortest-common-supersequence)
-  * `A` [Problème de Sac à Dos](src/algorithms/sets/knapsack-problem)
-  * `A` [Partition Entière](src/algorithms/math/integer-partition)
-  * `A` [Sous-partie Maximum](src/algorithms/sets/maximum-subarray)
-  * `A` [Algorithme de Bellman-Ford](src/algorithms/graph/bellman-ford) - trouver tous les plus courts chemins  partant d'un noeud vers tous les autres noeuds dans un graphe
-  * `A` [Algorithme de Floyd-Warshall](src/algorithms/graph/floyd-warshall) - trouver tous les plus courts chemins  entre toutes les paires de noeuds dans un graphe
-  * `A` [Expression Régulière](src/algorithms/string/regular-expression-matching)
-* **Retour sur trace** - de même que la version "Force Brute", essaie de générer toutes les solutions possibles, mais pour chaque solution générée, on teste si elle satisfait toutes les conditions, et seulement ensuite continuer à générer des solutions ultérieures. Sinon, l'on revient en arrière, et l'on essaie un
-chemin différent pour tester d'autres solutions. Normalement, la traversée en profondeur de l'espace d'états est utilisée.
-  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
-  * `B` [Unique Paths](src/algorithms/uncategorized/unique-paths)
-  * `A` [Hamiltonian Cycle](src/algorithms/graph/hamiltonian-cycle) - Visit every vertex exactly once
-  * `A` [Problème des N-Dames](src/algorithms/uncategorized/n-queens)
-  * `A` [Problème du Cavalier](src/algorithms/uncategorized/knight-tour)
-  * `A` [Somme combinatoire](src/algorithms/sets/combination-sum) - trouve toutes les combinaisons qui forment une somme spécifique
-* **Séparation et Evaluation** - pemet de retenir une solution à moindre coût dans un ensemble. Pour chaque étape, l'on garde une trace de la solution la moins coûteuse trouvée jusqu'à présent en tant que borne inférieure du coût. Cela afin d'éliminer les solutions partielles dont les coûts sont plus élevés que celui de la solution actuelle retenue. Normalement, la traversée en largeur en combinaison avec la traversée en profondeur de l'espace d'états de l'arbre est utilisée.
+- **Force Brute** - cherche parmi toutes les possibilités et retient la meilleure
+  - `B` [Recherche Linéaire](src/algorithms/search/linear-search)
+  - `A` [Sous-partie Maximum](src/algorithms/sets/maximum-subarray)
+  - `A` [Problème du Voyageur de Commerce](src/algorithms/graph/travelling-salesman) - chemin le plus court visitant chaque cité et retournant à la cité d'origine
+- **Gourmand** - choisit la meilleure option à l'instant courant, sans tenir compte de la situation future
+  - `B` [Jump Game](src/algorithms/uncategorized/jump-game)
+  - `A` [Problème du Sac à Dos Sans Contraintes](src/algorithms/sets/knapsack-problem)
+  - `A` [Algorithme de Dijkstra](src/algorithms/graph/dijkstra) - trouver tous les plus courts chemins partant d'un noeud vers tous les autres noeuds dans un graphe
+  - `A` [Algorithme de Prim](src/algorithms/graph/prim) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
+  - `A` [Algorithme de Kruskal](src/algorithms/graph/kruskal) - trouver l'arbre couvrant de poids minimal sur un graphe pondéré non dirigé
+- **Diviser et Régner** - divise le problème en sous problèmes (plus simples) et résoud ces sous problèmes
+  - `B` [Recherche Binaire](src/algorithms/search/binary-search)
+  - `B` [Tours de Hanoi](src/algorithms/uncategorized/hanoi-tower)
+  - `B` [Triangle de Pascal](src/algorithms/math/pascal-triangle)
+  - `B` [Algorithme d'Euclide](src/algorithms/math/euclidean-algorithm) - calcule le Plus Grand Commun Diviseur (PGCD)
+  - `B` [Tri Fusion](src/algorithms/sorting/merge-sort)
+  - `B` [Tri Rapide](src/algorithms/sorting/quick-sort)
+  - `B` [Arbre de Parcours en Profondeur](src/algorithms/tree/depth-first-search) (DFS)
+  - `B` [Graphe de Parcours en Profondeur](src/algorithms/graph/depth-first-search) (DFS)
+  - `B` [Jump Game](src/algorithms/uncategorized/jump-game)
+  - `A` [Permutations](src/algorithms/sets/permutations) (avec et sans répétitions)
+  - `A` [Combinations](src/algorithms/sets/combinations) (avec et sans répétitions)
+- **Programmation Dynamique** - construit une solution en utilisant les solutions précédemment trouvées
+  - `B` [Nombre de Fibonacci](src/algorithms/math/fibonacci)
+  - `B` [Jump Game](src/algorithms/uncategorized/jump-game)
+  - `B` [Chemins Uniques](src/algorithms/uncategorized/unique-paths)
+  - `A` [Distance de Levenshtein](src/algorithms/string/levenshtein-distance) - distance minimale d'édition entre deux séquences
+  - `A` [Plus Longue Sous-séquence Commune](src/algorithms/sets/longest-common-subsequence)
+  - `A` [Plus Longue Sous-chaîne Commune](src/algorithms/string/longest-common-substring)
+  - `A` [Plus Longue Sous-suite strictement croissante](src/algorithms/sets/longest-increasing-subsequence)
+  - `A` [Plus Courte Super-séquence Commune](src/algorithms/sets/shortest-common-supersequence)
+  - `A` [Problème de Sac à Dos](src/algorithms/sets/knapsack-problem)
+  - `A` [Partition Entière](src/algorithms/math/integer-partition)
+  - `A` [Sous-partie Maximum](src/algorithms/sets/maximum-subarray)
+  - `A` [Algorithme de Bellman-Ford](src/algorithms/graph/bellman-ford) - trouver tous les plus courts chemins partant d'un noeud vers tous les autres noeuds dans un graphe
+  - `A` [Algorithme de Floyd-Warshall](src/algorithms/graph/floyd-warshall) - trouver tous les plus courts chemins entre toutes les paires de noeuds dans un graphe
+  - `A` [Expression Régulière](src/algorithms/string/regular-expression-matching)
+- **Retour sur trace** - de même que la version "Force Brute", essaie de générer toutes les solutions possibles, mais pour chaque solution générée, on teste si elle satisfait toutes les conditions, et seulement ensuite continuer à générer des solutions ultérieures. Sinon, l'on revient en arrière, et l'on essaie un
+  chemin différent pour tester d'autres solutions. Normalement, la traversée en profondeur de l'espace d'états est utilisée.
+  - `B` [Jump Game](src/algorithms/uncategorized/jump-game)
+  - `B` [Unique Paths](src/algorithms/uncategorized/unique-paths)
+  - `A` [Hamiltonian Cycle](src/algorithms/graph/hamiltonian-cycle) - Visit every vertex exactly once
+  - `A` [Problème des N-Dames](src/algorithms/uncategorized/n-queens)
+  - `A` [Problème du Cavalier](src/algorithms/uncategorized/knight-tour)
+  - `A` [Somme combinatoire](src/algorithms/sets/combination-sum) - trouve toutes les combinaisons qui forment une somme spécifique
+- **Séparation et Evaluation** - pemet de retenir une solution à moindre coût dans un ensemble. Pour chaque étape, l'on garde une trace de la solution la moins coûteuse trouvée jusqu'à présent en tant que borne inférieure du coût. Cela afin d'éliminer les solutions partielles dont les coûts sont plus élevés que celui de la solution actuelle retenue. Normalement, la traversée en largeur en combinaison avec la traversée en profondeur de l'espace d'états de l'arbre est utilisée.
 
 ## Comment utiliser ce dépôt
 
 **Installer toutes les dépendances**
+
 ```
 npm install
 ```
@@ -203,22 +210,24 @@ npm run lint
 ```
 
 **Exécuter tous les tests**
+
 ```
 npm test
 ```
 
 **Exécuter les tests par nom**
+
 ```
 npm test -- 'LinkedList'
 ```
 
 **Tests personnalisés**
 
-Vous pouvez manipuler les structures de données et algorithmes présents dans ce 
-dépôt avec le fichier `./src/playground/playground.js` et écrire vos propres 
+Vous pouvez manipuler les structures de données et algorithmes présents dans ce
+dépôt avec le fichier `./src/playground/playground.js` et écrire vos propres
 tests dans file `./src/playground/__test__/playground.test.js`.
 
-Vous pourrez alors simplement exécuter la commande suivante afin de tester si 
+Vous pourrez alors simplement exécuter la commande suivante afin de tester si
 votre code fonctionne comme escompté
 
 ```
@@ -239,44 +248,44 @@ Comparaison de la performance d'algorithmes en notation Grand O.
 
 Source: [Big O Cheat Sheet](http://bigocheatsheet.com/).
 
-Voici la liste de certaines des notations Grand O les plus utilisées et de leurs 
+Voici la liste de certaines des notations Grand O les plus utilisées et de leurs
 comparaisons de performance suivant différentes tailles pour les données d'entrée.
 
-| Notation Grand O | Opérations pour 10 éléments  | Opérations pour 100 éléments  | Opérations pour 1000 éléments   |
-| ---------------- | ---------------------------- | ----------------------------- | ------------------------------- |
-| **O(1)**         | 1                            | 1                             | 1                               |
-| **O(log N)**     | 3                            | 6                             | 9                               |
-| **O(N)**         | 10                           | 100                           | 1000                            |
-| **O(N log N)**   | 30                           | 600                           | 9000                            |
-| **O(N^2)**       | 100                          | 10000                         | 1000000                         |
-| **O(2^N)**       | 1024                         | 1.26e+29                      | 1.07e+301                       |
-| **O(N!)**        | 3628800                      | 9.3e+157                      | 4.02e+2567                      |
+| Notation Grand O | Opérations pour 10 éléments | Opérations pour 100 éléments | Opérations pour 1000 éléments |
+| ---------------- | --------------------------- | ---------------------------- | ----------------------------- |
+| **O(1)**         | 1                           | 1                            | 1                             |
+| **O(log N)**     | 3                           | 6                            | 9                             |
+| **O(N)**         | 10                          | 100                          | 1000                          |
+| **O(N log N)**   | 30                          | 600                          | 9000                          |
+| **O(N^2)**       | 100                         | 10000                        | 1000000                       |
+| **O(2^N)**       | 1024                        | 1.26e+29                     | 1.07e+301                     |
+| **O(N!)**        | 3628800                     | 9.3e+157                     | 4.02e+2567                    |
 
 ### Complexité des Opérations suivant les Structures de Données
 
-| Structure de donnée             | Accès     | Recherche | Insertion | Suppression  | Commentaires  |
-| ------------------------------- | :-------: | :-------: | :-------: | :----------: | :------------ |
-| **Liste**                       | 1         | n         | n         | n            |               |
-| **Pile**                        | n         | n         | 1         | 1            |               |
-| **Queue**                       | n         | n         | 1         | 1            |               |
-| **Liste Liée**                  | n         | n         | 1         | 1            |               |
-| **Table de Hachage**            | -         | n         | n         | n            | Dans le cas des fonctions de hachage parfaites, les couts seraient de O(1) |
-| **Arbre de Recherche Binaire**  | n         | n         | n         | n            | Dans le cas des arbre équilibrés, les coûts seraient de O(log(n)) |
-| **Arbre B**                     | log(n)    | log(n)    | log(n)    | log(n)       |               |
-| **Arbre Red-Black**             | log(n)    | log(n)    | log(n)    | log(n)       |               |
-| **Arbre AVL**                   | log(n)    | log(n)    | log(n)    | log(n)       |               |
-| **Filtre de Bloom**             | -         | 1         | 1         | -            | Les faux positifs sont possibles lors de la recherche |
+| Structure de donnée            | Accès  | Recherche | Insertion | Suppression | Commentaires                                                               |
+| ------------------------------ | :----: | :-------: | :-------: | :---------: | :------------------------------------------------------------------------- |
+| **Liste**                      |   1    |     n     |     n     |      n      |                                                                            |
+| **Pile**                       |   n    |     n     |     1     |      1      |                                                                            |
+| **Queue**                      |   n    |     n     |     1     |      1      |                                                                            |
+| **Liste Liée**                 |   n    |     n     |     1     |      1      |                                                                            |
+| **Table de Hachage**           |   -    |     n     |     n     |      n      | Dans le cas des fonctions de hachage parfaites, les couts seraient de O(1) |
+| **Arbre de Recherche Binaire** |   n    |     n     |     n     |      n      | Dans le cas des arbre équilibrés, les coûts seraient de O(log(n))          |
+| **Arbre B**                    | log(n) |  log(n)   |  log(n)   |   log(n)    |                                                                            |
+| **Arbre Red-Black**            | log(n) |  log(n)   |  log(n)   |   log(n)    |                                                                            |
+| **Arbre AVL**                  | log(n) |  log(n)   |  log(n)   |   log(n)    |                                                                            |
+| **Filtre de Bloom**            |   -    |     1     |     1     |      -      | Les faux positifs sont possibles lors de la recherche                      |
 
 ### Complexité des Algorithmes de Tri de Liste
 
-| Nom                     | Meilleur        | Moyenne                | Pire                | Mémoire   | Stable    | Commentaires  |
-| ----------------------- | :-------------: | :--------------------: | :-----------------: | :-------: | :-------: | :------------ |
-| **Tri Bulle**           | n               | n<sup>2</sup>          | n<sup>2</sup>       | 1         | Oui       |               |
-| **Tri Insertion**       | n               | n<sup>2</sup>          | n<sup>2</sup>       | 1         | Oui       |               |
-| **Tri Sélection**       | n<sup>2</sup>   | n<sup>2</sup>          | n<sup>2</sup>       | 1         | Non       |               |
-| **Tri par Tas**         | n&nbsp;log(n)   | n&nbsp;log(n)          | n&nbsp;log(n)       | 1         | Non       |               |
-| **Merge sort**          | n&nbsp;log(n)   | n&nbsp;log(n)          | n&nbsp;log(n)       | n         | Oui       |               |
-| **Tri Rapide**          | n&nbsp;log(n)   | n&nbsp;log(n)          | n<sup>2</sup>       | log(n)    | Non       | le Tri Rapide est généralement effectué *in-place* avec une pile de taille O(log(n)) |
-| **Tri Shell**           | n&nbsp;log(n)   | dépend du gap séquence | n&nbsp;(log(n))<sup>2</sup>  | 1         | Non         |           |
-| **Tri Comptage**        | n + r           | n + r                  | n + r               | n + r     | Oui       | r - le plus grand nombre dans la liste |
-| **Tri Radix**           | n * k           | n * k                  | n * k               | n + k     | Non       | k - longueur du plus long index |
+| Nom               |   Meilleur    |        Moyenne         |            Pire             | Mémoire | Stable | Commentaires                                                                         |
+| ----------------- | :-----------: | :--------------------: | :-------------------------: | :-----: | :----: | :----------------------------------------------------------------------------------- |
+| **Tri Bulle**     |       n       |     n<sup>2</sup>      |        n<sup>2</sup>        |    1    |  Oui   |                                                                                      |
+| **Tri Insertion** |       n       |     n<sup>2</sup>      |        n<sup>2</sup>        |    1    |  Oui   |                                                                                      |
+| **Tri Sélection** | n<sup>2</sup> |     n<sup>2</sup>      |        n<sup>2</sup>        |    1    |  Non   |                                                                                      |
+| **Tri par Tas**   | n&nbsp;log(n) |     n&nbsp;log(n)      |        n&nbsp;log(n)        |    1    |  Non   |                                                                                      |
+| **Merge sort**    | n&nbsp;log(n) |     n&nbsp;log(n)      |        n&nbsp;log(n)        |    n    |  Oui   |                                                                                      |
+| **Tri Rapide**    | n&nbsp;log(n) |     n&nbsp;log(n)      |        n<sup>2</sup>        | log(n)  |  Non   | le Tri Rapide est généralement effectué _in-place_ avec une pile de taille O(log(n)) |
+| **Tri Shell**     | n&nbsp;log(n) | dépend du gap séquence | n&nbsp;(log(n))<sup>2</sup> |    1    |  Non   |                                                                                      |
+| **Tri Comptage**  |     n + r     |         n + r          |            n + r            |  n + r  |  Oui   | r - le plus grand nombre dans la liste                                               |
+| **Tri Radix**     |    n \* k     |         n \* k         |           n \* k            |  n + k  |  Non   | k - longueur du plus long index                                                      |

README.it-IT.md

@@ -0,0 +1,295 @@
+# Algoritmi e Strutture Dati in Javascript
+
+[![CI](https://github.com/trekhleb/javascript-algorithms/workflows/CI/badge.svg)](https://github.com/trekhleb/javascript-algorithms/actions)
+[![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)
+
+Questa repository contiene esempi in Javascript dei più popolari algoritmi e strutture dati .
+
+Ogni algortimo e struttura dati ha il suo README separato e la relative spiegazioni e i link per ulteriori approfondimenti (compresi quelli su YouTube).
+
+_Leggilo in altre lingue:_
+[_简体中文_](README.zh-CN.md),
+[_繁體中文_](README.zh-TW.md),
+[_한국어_](README.ko-KR.md),
+[_日本語_](README.ja-JP.md),
+[_Polski_](README.pl-PL.md),
+[_Français_](README.fr-FR.md),
+[_Español_](README.es-ES.md),
+[_Português_](README.pt-BR.md),
+[_Русский_](README.ru-RU.md),
+[_Türk_](README.tr-TR.md)
+
+*☝ Si noti che questo progetto è destinato ad essere utilizzato solo per l'apprendimento e la ricerca e non è destinato ad essere utilizzato per il commercio.*
+
+## Strutture Dati
+
+Una struttura dati è un particolare modo di organizzare e memorizzare i dati in un computer che  permeta di accedervi e modificarli in modo efficiente. Più precisamente, una struttura dati è una raccolta di dati, le relazioni tra di essi e le funzioni o operazioni che possono essere applicate ai dati.
+
+`P` - Principiante, `A` - Avanzato
+
+* `P` [Lista Concatenata](src/data-structures/linked-list)
+* `P` [Doppia Lista Concatenata](src/data-structures/doubly-linked-list)
+* `P` [Coda](src/data-structures/queue)
+* `P` [Pila](src/data-structures/stack)
+* `P` [Hash Table](src/data-structures/hash-table)
+* `P` [Heap](src/data-structures/heap) - versione massimo e minimo heap
+* `P` [Coda di priorità](src/data-structures/priority-queue)
+* `A` [Trie](src/data-structures/trie)
+* `A` [Albero](src/data-structures/tree)
+  * `A` [Albero binario di ricerca](src/data-structures/tree/binary-search-tree)
+  * `A` [Albero AVL](src/data-structures/tree/avl-tree)
+  * `A` [RB Albero](src/data-structures/tree/red-black-tree)
+  * `A` [Albero Segmentato](src/data-structures/tree/segment-tree) - con  min/max/sum esempi di query
+  * `A` [Albero di Fenwick](src/data-structures/tree/fenwick-tree) (Albero binario indicizzato)
+* `A` [Grafo](src/data-structures/graph) (direzionale e unidirezionale)
+* `A` [Set Disgiunto](src/data-structures/disjoint-set)
+* `A` [Filtro Bloom](src/data-structures/bloom-filter)
+
+## Algoritmi
+
+Un algoritmo è una specifica univoca per risolvere una classe di problemi. È
+un insieme di regole che definiscono con precisione una sequenza di operazioni.
+
+`P` - Principiante, `A` - Avanzato
+
+### Algoritmi per Topic
+
+* **Matematica**
+  * `P` [Manipolazione dei Bit](src/algorithms/math/bits) - set/get/update/clear bits, moltiplicazione/divisione per due, gestire numeri negativi etc.
+  * `P` [Fattoriale](src/algorithms/math/factorial) 
+  * `P` [Numeri di Fibonacci](src/algorithms/math/fibonacci) - classico e forma chiusa
+  * `P` [Test di Primalità](src/algorithms/math/primality-test) (metodo del divisore)
+  * `P` [Algoritmo di Euclide](src/algorithms/math/euclidean-algorithm) - trova il massimo comune divisore (MCD)
+  * `P` [Minimo Comune Multiplo](src/algorithms/math/least-common-multiple) (MCM)
+  * `P` [Crivello di Eratostene](src/algorithms/math/sieve-of-eratosthenes) - trova i numeri i primi fino al limite indicato
+  * `P` [Potenza di due](src/algorithms/math/is-power-of-two) - controlla se il numero è una potenza di due
+  * `P` [Triangolo di Pascal](src/algorithms/math/pascal-triangle)
+  * `P` [Numeri Complessi](src/algorithms/math/complex-number) - numeri complessi e operazioni 
+  * `P` [Radiante & Gradi](src/algorithms/math/radian) - conversione da radiante a gradi e viceversa
+  * `P` [Potenza di un Numero](src/algorithms/math/fast-powering)
+  * `A` [Partizione di un Intero](src/algorithms/math/integer-partition)
+  * `A` [Radice Quadrata](src/algorithms/math/square-root) - Metodo di Newton
+  * `A` [Algoritmo di Liu Hui π](src/algorithms/math/liu-hui) - calcolare π usando un poligono
+  * `A` [Trasformata Discreta di Fourier ](src/algorithms/math/fourier-transform) -decomporre una funzione di tempo (un segnale) nelle frequenze che lo compongono 
+* **Set**
+  * `P` [Prodotto Cartesiano](src/algorithms/sets/cartesian-product) - moltiplicazione multipla di set
+  * `P` [Fisher–Yates Shuffle](src/algorithms/sets/fisher-yates) - permutazione casuale di un sequenza finita
+  * `A` [Power Set](src/algorithms/sets/power-set) - tutti i sottoinsiemi di un set (soluzioni bitwise e backtracking)
+  * `A` [Permutazioni](src/algorithms/sets/permutations) (con e senza ripetizioni)
+  * `A` [Combinazioni](src/algorithms/sets/combinations) (con e senza ripetizioni)
+  * `A` [Massima Sottosequenza Comune](src/algorithms/sets/longest-common-subsequence) (LCS)
+  * `A` [Massima Sottosequenza Crescente](src/algorithms/sets/longest-increasing-subsequence)
+  * `A` [Minima Sottosequenza Diffusa](src/algorithms/sets/shortest-common-supersequence) (SCS)
+  * `A` [Problema dello Zaino di Knapsack](src/algorithms/sets/knapsack-problem) - "0/1" e "Senza Restrizioni"
+  * `A` [Massimo SubArray](src/algorithms/sets/maximum-subarray) - "Brute Force" e "Programmazione Dinamica" versione Kadane
+  * `A` [Somma di Combinazioni](src/algorithms/sets/combination-sum) - ricerca di tutte le combinazioni di una somma
+* **String**
+  * `P` [Distanza di Hamming](src/algorithms/string/hamming-distance) - numero di posizioni in cui i caratteri sono diversi
+  * `A` [Distanza di Levenshtein](src/algorithms/string/levenshtein-distance) - numero minimo di modifiche per rendere uguali due stringhe
+  * `A` [Algoritmo di Knuth-Morris-Pratt](src/algorithms/string/knuth-morris-pratt) (KMP) - ricerca nella sottostringa (pattern matching)
+  * `A` [Algoritmo Z](src/algorithms/string/z-algorithm) - ricerca nella sottostringa (pattern matching)
+  * `A` [Algoritmo di Rabin Karp ](src/algorithms/string/rabin-karp) - ricerca nella sottostringa
+  * `A` [Sottostringa Comune più lunga](src/algorithms/string/longest-common-substring)
+  * `A` [Espressioni Regolari](src/algorithms/string/regular-expression-matching)
+* **Searches**
+  * `P` [Ricerca Sequenziale](src/algorithms/search/linear-search)
+  * `P` [Ricerca a Salti](src/algorithms/search/jump-search) (o Ricerca a Blocchi) - per la ricerca in array ordinati
+  * `P` [Ricerca Binari](src/algorithms/search/binary-search) - per la ricerca in array ordinati
+  * `P` [Ricerca Interpolata](src/algorithms/search/interpolation-search) - per la ricerca in un array ordinato uniformemente distibuito
+* **Sorting**
+  * `P` [Bubble Sort](src/algorithms/sorting/bubble-sort)
+  * `P` [Selection Sort](src/algorithms/sorting/selection-sort)
+  * `P` [Insertion Sort](src/algorithms/sorting/insertion-sort)
+  * `P` [Heap Sort](src/algorithms/sorting/heap-sort)
+  * `P` [Merge Sort](src/algorithms/sorting/merge-sort)
+  * `P` [Quicksort](src/algorithms/sorting/quick-sort) - con e senza allocazione di ulteriore memoria
+  * `P` [Shellsort](src/algorithms/sorting/shell-sort)
+  * `P` [Counting Sort](src/algorithms/sorting/counting-sort)
+  * `P` [Radix Sort](src/algorithms/sorting/radix-sort)
+* **Lista Concatenatas**
+  * `P` [Attraversamento Lista Concatenata](src/algorithms/linked-list/traversal)
+  * `P` [Attraversamento Lista Concatenata nel senso Contrario](src/algorithms/linked-list/reverse-traversal)
+* **Alberi**
+  * `P` [Ricerca in Profondità su Alberi](src/algorithms/tree/depth-first-search) (DFS)
+  * `P` [Ricerca in Ampiezza su Alberi](src/algorithms/tree/breadth-first-search) (BFS)
+* **Grafi**
+  * `P` [Ricerca in Profondità su Grafi](src/algorithms/graph/depth-first-search) (DFS)
+  * `P` [Breadth-First Search su Grafi](src/algorithms/graph/breadth-first-search) (BFS)
+  * `P` [Algoritmo di Kruskal](src/algorithms/graph/kruskal) - ricerca dell'Albero con Minima Distanza (MST) per grafi pesati unidirezionali
+  * `A` [Algoritmo di Dijkstra](src/algorithms/graph/dijkstra) - ricerca dei percorsi più breve per raggiungere tutti i vertici del grafo da un singolo vertice 
+  * `A` [Algoritmo di Bellman-Ford](src/algorithms/graph/bellman-ford) - ricerca dei percorsi più breve per raggiungere tutti i vertici del grafo da un singolo vertice 
+  * `A` [Algoritmo di Floyd-Warshall](src/algorithms/graph/floyd-warshall) -  ricerca dei percorsi più brevi tra tutte le coppie di vertici
+  * `A` [Rivelamento dei Cicli](src/algorithms/graph/detect-cycle) - per grafici diretti e non diretti (basate su partizioni DFS e Disjoint Set)
+  * `A` [Algoritmo di Prim](src/algorithms/graph/prim) - ricerca dell'Albero Ricoprente Minimo (MST) per grafi unidirezionali pesati
+  * `A` [Ordinamento Topologico](src/algorithms/graph/topological-sorting) - metodo DFS
+  * `A` [Punti di Articolazione](src/algorithms/graph/articulation-points) - Algoritmo di Tarjan (basato su DFS)
+  * `A` [Bridges](src/algorithms/graph/bridges) - basato su DFS
+  * `A` [Cammino Euleriano e Circuito Euleriano](src/algorithms/graph/eulerian-path) - Algoritmo di Fleury - Visita ogni margine esattamente una volta
+  * `A` [Ciclo di Hamiltonian](src/algorithms/graph/hamiltonian-cycle) - Visita ad ogni vertice solo una volta
+  * `A` [Componenti Fortemente Connessa](src/algorithms/graph/strongly-connected-components) - algoritmo di Kosaraju
+  * `A` [Problema del Commesso Viaggiatore](src/algorithms/graph/travelling-salesman) - il percorso più breve che visita ogni città e ritorna alla città iniziale
+* **Crittografia**
+  * `P` [Hash Polinomiale](src/algorithms/cryptography/polynomial-hash) - Una funzione hash di rolling basata sul polinomio 
+* **Senza categoria**
+  * `P` [Torre di Hanoi](src/algorithms/uncategorized/hanoi-tower)
+  * `P` [Rotazione Matrice Quadrata](src/algorithms/uncategorized/square-matrix-rotation) - algoritmo in memoria
+  * `P` [Jump Game](src/algorithms/uncategorized/jump-game) - backtracking, programmazione dinamica (top-down + bottom-up) ed esempre di greeedy
+  * `P` [Percorsi Unici](src/algorithms/uncategorized/unique-paths) - backtracking, programmazione dinamica and l'esempio del Triangolo di Pascal  
+  * `P` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - problema dell'acqua piovana in trappola(versione con programmazione dinamica e brute force)
+  * `P` [Recursive Staircase](src/algorithms/uncategorized/recursive-staircase) - contare il numero di percorsi per arrivare in vetta(4 soluzioni)
+  * `A` [Rompicapo delle Otto Regine](src/algorithms/uncategorized/n-queens)
+  * `A` [Percorso del Cavallo](src/algorithms/uncategorized/knight-tour)
+
+### Modelli di Algoritmi
+
+ Un modello di algoritmo è un generico metodo o approcio che sta alla base della progettazione di una classe di algoritmi.
+ Si tratta di un'astrazione ancora più alta di un algoritmo, proprio come un algoritmo è un'astrazione di un programma del computer.
+
+* **Brute Force** - controlla tutte le possibilità e seleziona la migliore
+  * `P` [Ricerca Lineare](src/algorithms/search/linear-search)
+  * `P` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - problema dell'acqua piovana in trappola
+  * `P` [Recursive Staircase](src/algorithms/uncategorized/recursive-staircase) - contare il numero di percorsi per arrivare in vetta
+  * `A` [Massimo SubArray](src/algorithms/sets/maximum-subarray)
+  * `A` [Problema del commesso viaggiatore](src/algorithms/graph/travelling-salesman) - il percorso più breve che visita ogni città e ritorna alla città iniziale
+  * `A` [Trasformata Discreta di Fourier](src/algorithms/math/fourier-transform) - scomporre la funzione (segnale) del tempo in frequenze che la compongono 
+* **Greedy** - scegliere l'opzione migliore al momento d'eleborazione dell'algoritmo, senza alcuna considerazione per il futuro
+  * `P` [Jump Game](src/algorithms/uncategorized/jump-game)
+  * `A` [Problema dello Zaino di Knapsack](src/algorithms/sets/knapsack-problem)
+  * `A` [Algoritmo di Dijkstra](src/algorithms/graph/dijkstra) - ricerca del percorso più breve tra tutti i vertici del grafo
+  * `A` [Algoritmo di Prim](src/algorithms/graph/prim) - ricerca del Minimo Albero Ricoprente per grafi pesati e unidirezionali 
+  * `A` [Kruskal’s Algorithm](src/algorithms/graph/kruskal) - finding Minimum Spanning Tree (MST) for weighted undirected graph
+* **Divide e Conquista** - divide il problema in piccole parti e risolve ogni parte 
+  * `P` [Ricerca Binaria](src/algorithms/search/binary-search)
+  * `P` [Torre di Hanoi](src/algorithms/uncategorized/hanoi-tower)
+  * `P` [Triangolo di Pascal](src/algorithms/math/pascal-triangle)
+  * `P` [Algoritmo di Euclide](src/algorithms/math/euclidean-algorithm) - calculate the Greatest Common Divisor (GCD)
+  * `P` [Merge Sort](src/algorithms/sorting/merge-sort)
+  * `P` [Quicksort](src/algorithms/sorting/quick-sort)
+  * `P` [Albero per Ricerca in Profondità](src/algorithms/tree/depth-first-search) (DFS)
+  * `P` [Grafo per Ricerca in Profondità](src/algorithms/graph/depth-first-search) (DFS)
+  * `P` [Jump Game](src/algorithms/uncategorized/jump-game)
+  * `P` [Algoritmo di Elevamento a Potenza](src/algorithms/math/fast-powering)
+  * `A` [Permutazioni](src/algorithms/sets/permutations) (con o senza ripetizioni)
+  * `A` [Combinazioni](src/algorithms/sets/combinations) (con o senza ripetizioni)
+* **Programmazione Dinamica** - creare una soluzione utilizzando le sub-solution trovate in precedenza
+  * `P` [Numero di Fibonacci](src/algorithms/math/fibonacci)
+  * `P` [Jump Game](src/algorithms/uncategorized/jump-game)
+  * `P` [Percorsi Unici](src/algorithms/uncategorized/unique-paths)
+  * `P` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - problema dell'acqua piovana in trappola
+  * `P` [Recursive Staircase](src/algorithms/uncategorized/recursive-staircase) - contare il numero di percorsi per arrivare in vetta
+  * `A` [Distanza di Levenshtein](src/algorithms/string/levenshtein-distance) - minima variazione tra due sequenze
+  * `A` [La Più Lunga Frequente SottoSequenza](src/algorithms/sets/longest-common-subsequence) (LCS)
+  * `A` [La Più Lunga Frequente SubString](src/algorithms/string/longest-common-substring)
+  * `A` [La Più Lunga SottoSequenza Crescente](src/algorithms/sets/longest-increasing-subsequence)
+  * `A` [La Più Corta e Frequente SuperSequenza](src/algorithms/sets/shortest-common-supersequence)
+  * `A` [Problema dello zaino](src/algorithms/sets/knapsack-problem)
+  * `A` [Partizione di un Intero](src/algorithms/math/integer-partition)
+  * `A` [Massimo SubArray](src/algorithms/sets/maximum-subarray)
+  * `A` [Algoritmo di Bellman-Ford](src/algorithms/graph/bellman-ford) - ricerca del percorso più breve per tutti i vertici del grafo
+  * `A` [Algoritmo di Floyd-Warshall](src/algorithms/graph/floyd-warshall) - ricerca del percorso più breve tra tutte le coppie di vertici 
+  * `A` [Espressioni Regolari](src/algorithms/string/regular-expression-matching)
+* **Backtracking** -  come la brute force, provate a generare tutte le soluzioni possibili, ma ogni volta che generate la prossima soluzione testate se soddisfa tutte le condizioni e solo allora continuare a generare soluzioni successive. Altrimenti, fate marcia indietro, e andate su un percorso diverso per trovare una soluzione. Normalmente si utilizza l'algoritmo DFS.
+  * `P` [Jump Game](src/algorithms/uncategorized/jump-game)
+  * `P` [Percorsi Unici](src/algorithms/uncategorized/unique-paths)
+  * `P` [Power Set](src/algorithms/sets/power-set) - tutti i subset di un set
+  * `A` [Ciclo di Hamiltonian](src/algorithms/graph/hamiltonian-cycle) - visita di tutti i vertici solamente una volta
+  * `A` [Problema di N-Queens](src/algorithms/uncategorized/n-queens)
+  * `A` [Knight's Tour](src/algorithms/uncategorized/knight-tour)
+  * `A` [Combinazioni di una Somma](src/algorithms/sets/combination-sum) - trovare tutte le combinazioni che compongono una somma
+* **Branch & Bound** - ricordatevi che la soluzione meno costosa trovata ad ogni step durante il backtracking e
+il costo di usare la soluzione meno costosa trovata fino al limite inferiore al costo minimo della soluzione al problema,
+al fine di scartare soluzioni parziali con costi maggiori della soluzione meno costosa trovata .
+Di solito si usa BFS trasversale in combinazione con DFS trasversale .
+
+## Come usare questa repository
+
+**Installare tutte le dipendenze**
+```
+npm install
+```
+
+**Eseguire ESLint**
+
+Potresti usarlo per controllare la qualità del codice.
+
+```
+npm run lint
+```
+
+**Eseguire tutti i test**
+```
+npm test
+```
+
+**Eseguire un test tramite il nome**
+```
+npm test -- 'LinkedList'
+```
+
+**Playground**
+
+Se vuoi puoi giocare le strutture dati e gli algoritmi nel file ./src/playground/playground.js` e 
+scrivere test nel file `./src/playground/__test__/playground.test.js`.
+
+Poi puoi semplicemente eseguire il seguente comando per testare quello che hai scritto : 
+
+```
+npm test -- 'playground'
+```
+
+## Informazioni Utili
+
+### Bibliografia
+
+[▶ Data Structures and Algorithms on YouTube](https://www.youtube.com/playlist?list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+
+### Notazione Big O 
+
+* La notazione Big O* è usata per classificare algoritmi in base al tempo di esecuzione o ai 
+requisiti di spazio che crescono in base alla crescita dell'input .
+Nella grafico qua sotto puoi trovare gli ordini di crescita più comuni degli algoritmi usando la notazione Big O.
+
+![Grafi Big O ](./assets/big-o-graph.png)
+
+Riferimento: [Big O Cheat Sheet](http://bigocheatsheet.com/).
+
+Nella tabella qua sotto ci sono riportate la lista delle notazioni Big O più usate e delle loro prestazioni comparate tra differenti grandezze d'input .
+
+| Notazione Big O | Computazione con 10 elementi | Computazione con 100 elementi | Computazione con 1000 elementi  |
+| --------------- | ---------------------------- | ----------------------------- | ------------------------------- |
+| **O(1)**        | 1                            | 1                             | 1                               |
+| **O(log N)**    | 3                            | 6                             | 9                               |
+| **O(N)**        | 10                           | 100                           | 1000                            |
+| **O(N log N)**  | 30                           | 600                           | 9000                            |
+| **O(N^2)**      | 100                          | 10000                         | 1000000                         |
+| **O(2^N)**      | 1024                         | 1.26e+29                      | 1.07e+301                       |
+| **O(N!)**       | 3628800                      | 9.3e+157                      | 4.02e+2567                      |
+
+### Complessità delle Operazion sulle Strutture Dati
+
+| Struttura Dati          | Accesso   | Ricerca   | Inserimento | Rimozione | Commenti  |
+| ----------------------- | :-------: | :-------: | :--------:  | :-------: | :-------- |
+| **Array**               | 1         | n         | n           | n         |           |
+| **Pila**                | n         | n         | 1           | 1         |           |
+| **Coda**                | n         | n         | 1           | 1         |           |
+| **Lista Concatenata**   | n         | n         | 1           | n         |           |
+| **Tabella Hash**        | -         | n         | n           | n         | Nel caso di una funzione di hashing perfetta il costo sarebbe O(1)|
+| **Binary Search Tree**  | n         | n         | n           | n         | Nel caso di albero bilanciato il costo sarebbe O(log(n)) |
+| **B-Tree**              | log(n)    | log(n)    | log(n)      | log(n)    |           |
+| **Red-Black Tree**      | log(n)    | log(n)    | log(n)      | log(n)    |           |
+| **Albero AVL**          | log(n)    | log(n)    | log(n)      | log(n)    |           |
+| **Bloom Filter**        | -         | 1         | 1           | -         | Falsi positivi sono possibili durante la ricerca |
+
+### Complessità degli Algoritmi di Ordinamento di Array
+
+| Nome                  | Milgiore        | Media               | Perggiore           | Memoria   | Stabile   | Commenti  |
+| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
+| **Bubble sort**       | n               | n<sup>2</sup>       | n<sup>2</sup>       | 1         | Yes       |           |
+| **Insertion sort**    | n               | n<sup>2</sup>       | n<sup>2</sup>       | 1         | Yes       |           |
+| **Selection sort**    | n<sup>2</sup>   | n<sup>2</sup>       | n<sup>2</sup>       | 1         | No        |           |
+| **Heap sort**         | n&nbsp;log(n)   | n&nbsp;log(n)       | n&nbsp;log(n)       | 1         | No        |           |
+| **Merge sort**        | n&nbsp;log(n)   | n&nbsp;log(n)       | n&nbsp;log(n)       | n         | Yes       |           |
+| **Quick sort**        | n&nbsp;log(n)   | n&nbsp;log(n)       | n<sup>2</sup>       | log(n)    | No        | Quicksort viene eseguito in memoria solitamente con una pila di O(log(n)) |
+| **Shell sort**        | n&nbsp;log(n)   | dipende dagli spazi vuoti nella sequenza  | n&nbsp;(log(n))<sup>2</sup>  | 1         | No         |           |
+| **Counting sort**     | n + r           | n + r               | n + r               | n + r     | Yes       | r - numero più grande nell'array |
+| **Radix sort**        | n * k           | n * k               | n * k               | n + k     | Yes       | k - lunghezza della chiave più grande |

README.ja-JP.md

@@ -1,6 +1,6 @@
 # JavaScriptアルゴリズムとデータ構造
 
-[![Build Status](https://travis-ci.org/trekhleb/javascript-algorithms.svg?branch=master)](https://travis-ci.org/trekhleb/javascript-algorithms)
+[![CI](https://github.com/trekhleb/javascript-algorithms/workflows/CI/badge.svg)](https://github.com/trekhleb/javascript-algorithms/actions)
 [![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)
 
 このリポジトリには、JavaScriptベースの一般的なアルゴリズムとデータ構造に関する多数のサンプルが含まれています。
@@ -17,7 +17,10 @@ _Read this in other languages:_
 [_Polski_](README.pl-PL.md),
 [_Français_](README.fr-FR.md),
 [_Español_](README.es-ES.md),
-[_Português_](README.pt-BR.md)
+[_Português_](README.pt-BR.md),
+[_Русский_](README.ru-RU.md),
+[_Türk_](README.tr-TR.md),
+[_Italiana_](README.it-IT.md)
 
 ## データ構造
 

README.ko-KR.md

@@ -1,6 +1,6 @@
 # JavaScript 알고리즘 및 자료 구조
 
-[![Build Status](https://travis-ci.org/trekhleb/javascript-algorithms.svg?branch=master)](https://travis-ci.org/trekhleb/javascript-algorithms)
+[![CI](https://github.com/trekhleb/javascript-algorithms/workflows/CI/badge.svg)](https://github.com/trekhleb/javascript-algorithms/actions)
 [![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)
 
 이 저장소에는 많이 알려진 알고리즘 및 자료 구조의 Javascript 기반 예제를 담고 있습니다.
@@ -16,7 +16,10 @@ _Read this in other languages:_
 [_Polski_](README.pl-PL.md),
 [_Français_](README.fr-FR.md),
 [_Español_](README.es-ES.md),
-[_Português_](README.pt-BR.md)
+[_Português_](README.pt-BR.md),
+[_Русский_](README.ru-RU.md),
+[_Türk_](README.tr-TR.md),
+[_Italiana_](README.it-IT.md)
 
 ## 자료 구조
 

README.md

@@ -1,6 +1,6 @@
 # JavaScript Algorithms and Data Structures
 
-[![Build Status](https://travis-ci.org/trekhleb/javascript-algorithms.svg?branch=master)](https://travis-ci.org/trekhleb/javascript-algorithms)
+[![CI](https://github.com/trekhleb/javascript-algorithms/workflows/CI/badge.svg)](https://github.com/trekhleb/javascript-algorithms/actions)
 [![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)
 
 This repository contains JavaScript based examples of many
@@ -18,10 +18,13 @@ _Read this in other languages:_
 [_Polski_](README.pl-PL.md),
 [_Français_](README.fr-FR.md),
 [_Español_](README.es-ES.md),
-[_Português_](README.pt-BR.md)
+[_Português_](README.pt-BR.md),
+[_Русский_](README.ru-RU.md),
+[_Türk_](README.tr-TR.md),
+[_Italiana_](README.it-IT.md)
 
 *☝ Note that this project is meant to be used for learning and researching purposes 
-only and it is **not** meant to be used for production.*
+only, and it is **not** meant to be used for production.*
 
 ## Data Structures
 
@@ -63,6 +66,7 @@ a set of rules that precisely define a sequence of operations.
   * `B` [Bit Manipulation](src/algorithms/math/bits) - set/get/update/clear bits, multiplication/division by two, make negative etc.
   * `B` [Factorial](src/algorithms/math/factorial) 
   * `B` [Fibonacci Number](src/algorithms/math/fibonacci) - classic and closed-form versions
+  * `B` [Prime Factors](src/algorithms/math/prime-factors) - finding prime factors and counting them using Hardy-Ramanujan's theorem  
   * `B` [Primality Test](src/algorithms/math/primality-test) (trial division method)
   * `B` [Euclidean Algorithm](src/algorithms/math/euclidean-algorithm) - calculate the Greatest Common Divisor (GCD)
   * `B` [Least Common Multiple](src/algorithms/math/least-common-multiple) (LCM)
@@ -72,6 +76,7 @@ a set of rules that precisely define a sequence of operations.
   * `B` [Complex Number](src/algorithms/math/complex-number) - complex numbers and basic operations with them
   * `B` [Radian & Degree](src/algorithms/math/radian) - radians to degree and backwards conversion
   * `B` [Fast Powering](src/algorithms/math/fast-powering)
+  * `B` [Horner's method](src/algorithms/math/horner-method) - polynomial evaluation
   * `A` [Integer Partition](src/algorithms/math/integer-partition)
   * `A` [Square Root](src/algorithms/math/square-root) - Newton's method
   * `A` [Liu Hui π Algorithm](src/algorithms/math/liu-hui) - approximate π calculations based on N-gons
@@ -305,6 +310,8 @@ Below is the list of some of the most used Big O notations and their performance
 | **Counting sort**     | n + r           | n + r               | n + r               | n + r     | Yes       | r - biggest number in array |
 | **Radix sort**        | n * k           | n * k               | n * k               | n + k     | Yes       | k - length of longest key |
 
-## Supporting the project
+## Project Backers
 
-You may support this project via ❤️️ [GitHub](https://github.com/sponsors/trekhleb) or ❤️️ [Patreon](https://www.patreon.com/trekhleb).          
+> You may support this project via ❤️️ [GitHub](https://github.com/sponsors/trekhleb) or ❤️️ [Patreon](https://www.patreon.com/trekhleb).
+
+[Folks who are backing this project](https://github.com/trekhleb/javascript-algorithms/blob/master/BACKERS.md) `∑ = 1`

README.pl-PL.md

@@ -1,6 +1,6 @@
 # JavaScript Algorytmy i Struktury Danych
 
-[![Build Status](https://travis-ci.org/trekhleb/javascript-algorithms.svg?branch=master)](https://travis-ci.org/trekhleb/javascript-algorithms)
+[![CI](https://github.com/trekhleb/javascript-algorithms/workflows/CI/badge.svg)](https://github.com/trekhleb/javascript-algorithms/actions)
 [![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)
 
 To repozytorium zawiera wiele przykładów JavaScript opartych na 
@@ -18,7 +18,10 @@ _Read this in other languages:_
 [_日本語_](README.ja-JP.md),
 [_Français_](README.fr-FR.md),
 [_Español_](README.es-ES.md),
-[_Português_](README.pt-BR.md)
+[_Português_](README.pt-BR.md),
+[_Русский_](README.ru-RU.md),
+[_Türk_](README.tr-TR.md),
+[_Italiana_](README.it-IT.md)
 
 ## Struktury Danych
 

README.pt-BR.md

@@ -1,6 +1,6 @@
 # Estrutura de Dados e Algoritmos em JavaScript
 
-[![Build Status](https://travis-ci.org/trekhleb/javascript-algorithms.svg?branch=master)](https://travis-ci.org/trekhleb/javascript-algorithms)
+[![CI](https://github.com/trekhleb/javascript-algorithms/workflows/CI/badge.svg)](https://github.com/trekhleb/javascript-algorithms/actions)
 [![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)
 
 Este repositório contém exemplos baseados em JavaScript de muitos
@@ -18,9 +18,12 @@ _Leia isto em outros idiomas:_
 [_日本語_](README.ja-JP.md),
 [_Polski_](README.pl-PL.md),
 [_Français_](README.fr-FR.md),
-[_Español_](README.es-ES.md)
+[_Español_](README.es-ES.md),
+[_Русский_](README.ru-RU.md),
+[_Türk_](README.tr-TR.md),
+[_Italiana_](README.it-IT.md)
 
-## Data Structures
+## Estrutura de Dados
 
 Uma estrutura de dados é uma maneira particular de organizar e armazenar dados em um computador para que ele possa
 ser acessado e modificado de forma eficiente. Mais precisamente, uma estrutura de dados é uma coleção de dados

README.ru-RU.md

@@ -0,0 +1,293 @@
+# Алгоритмы и структуры данных на JavaScript
+
+[![CI](https://github.com/trekhleb/javascript-algorithms/workflows/CI/badge.svg)](https://github.com/trekhleb/javascript-algorithms/actions)
+[![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)
+
+В этом репозитории содержатся базовые JavaScript-примеры многих популярных алгоритмов и структур данных.
+
+Для каждого алгоритма и структуры данных есть свой файл README с соответствующими пояснениями и ссылками на материалы для дальнейшего изучения (в том числе и ссылки на видеоролики в YouTube).
+
+_Читать на других языках:_
+[_English_](https://github.com/trekhleb/javascript-algorithms/),
+[_简体中文_](README.zh-CN.md),
+[_繁體中文_](README.zh-TW.md),
+[_한국어_](README.ko-KR.md),
+[_日本語_](README.ja-JP.md),
+[_Polski_](README.pl-PL.md),
+[_Français_](README.fr-FR.md),
+[_Español_](README.es-ES.md),
+[_Português_](README.pt-BR.md),
+[_Türk_](README.tr-TR.md),
+[_Italiana_](README.it-IT.md)
+
+*☝ Замечание: этот репозиторий предназначен для учебно-исследовательских целей (**не** для использования в продакшн-системах).*
+
+## Структуры данных
+
+Структура данных (англ. data structure) — программная единица, позволяющая хранить и обрабатывать множество однотипных и/или логически связанных данных в вычислительной технике. Для добавления, поиска, изменения и удаления данных структура данных предоставляет некоторый набор функций, составляющих её интерфейс.
+
+`B` - Базовый уровень, `A` - Продвинутый уровень
+
+* `B` [Связный список](src/data-structures/linked-list)
+* `B` [Двунаправленный связный список](src/data-structures/doubly-linked-list)
+* `B` [Очередь](src/data-structures/queue)
+* `B` [Стек](src/data-structures/stack)
+* `B` [Хеш-табица](src/data-structures/hash-table)
+* `B` [Куча](src/data-structures/heap) — максимальная и минимальная версии
+* `B` [Очередь с приоритетом](src/data-structures/priority-queue)
+* `A` [Префиксное дерево](src/data-structures/trie)
+* `A` [Деревья](src/data-structures/tree)
+  * `A` [Двоичное дерево поиска](src/data-structures/tree/binary-search-tree)
+  * `A` [АВЛ-дерево](src/data-structures/tree/avl-tree)
+  * `A` [Красно-чёрное дерево](src/data-structures/tree/red-black-tree)
+  * `A` [Дерево отрезков](src/data-structures/tree/segment-tree) — для минимума, максимума и суммы отрезков
+  * `A` [Дерево Фенвика](src/data-structures/tree/fenwick-tree) (двоичное индексированное дерево)
+* `A` [Граф](src/data-structures/graph) (ориентированный и неориентированный)
+* `A` [Система непересекающихся множеств](src/data-structures/disjoint-set)
+* `A` [Фильтр Блума](src/data-structures/bloom-filter)
+
+## Алгоритмы
+
+Алгоритм — конечная совокупность точно заданных правил решения некоторого класса задач или набор инструкций, описывающих порядок действий исполнителя для решения некоторой задачи.
+
+`B` - Базовый уровень, `A` - Продвинутый уровень
+
+### Алгоритмы по тематике
+
+* **Математика**
+  * `B` [Битовые манипуляции](src/algorithms/math/bits) — получение/запись/сброс/обновление битов, умножение/деление на 2, сделать отрицательным и т.п.
+  * `B` [Факториал](src/algorithms/math/factorial) 
+  * `B` [Числа Фибоначчи](src/algorithms/math/fibonacci) — классическое решение, решение в замкнутой форме
+  * `B` [Тест простоты](src/algorithms/math/primality-test) (метод пробного деления)
+  * `B` [Алгоритм Евклида](src/algorithms/math/euclidean-algorithm) — нахождение наибольшего общего делителя (НОД)
+  * `B` [Наименьшее общее кратное](src/algorithms/math/least-common-multiple) (НОК)
+  * `B` [Решето Эратосфена](src/algorithms/math/sieve-of-eratosthenes) — нахождение всех простых чисел до некоторого целого числа n
+  * `B` [Степень двойки](src/algorithms/math/is-power-of-two) — является ли число степенью двойки (простое и побитовое решения)
+  * `B` [Треугольник Паскаля](src/algorithms/math/pascal-triangle)
+  * `B` [Комплексные числа](src/algorithms/math/complex-number) — комплексные числа, базовые операции над ними
+  * `B` [Радианы и градусы](src/algorithms/math/radian) — конвертирование радианов в градусы и наоборот
+  * `B` [Быстрое возведение в степень](src/algorithms/math/fast-powering)
+  * `A` [Разбиение числа](src/algorithms/math/integer-partition)
+  * `A` [Квадратный корень](src/algorithms/math/square-root) — метод Ньютона
+  * `A` [Алгоритм Лю Хуэя](src/algorithms/math/liu-hui) — расчёт числа π с заданной точностью методом вписанных правильных многоугольников
+  * `A` [Дискретное преобразование Фурье](src/algorithms/math/fourier-transform) — разложение временной функции (сигнала) на частотные составляющие 
+* **Множества**
+  * `B` [Декартово произведение](src/algorithms/sets/cartesian-product) — результат перемножения множеств
+  * `B` [Тасование Фишера — Йетса](src/algorithms/sets/fisher-yates) — создание случайных перестановок конечного множества
+  * `A` [Булеан](src/algorithms/sets/power-set) — все подмножества заданного множества (побитовый поиск и поиск с возвратом)
+  * `A` [Перестановки](src/algorithms/sets/permutations) (с повторениями и без повторений)
+  * `A` [Сочетания](src/algorithms/sets/combinations) (с повторениями и без повторений)
+  * `A` [Наибольшая общая подпоследовательность](src/algorithms/sets/longest-common-subsequence)
+  * `A` [Наибольшая увеличивающаяся подпоследовательность](src/algorithms/sets/longest-increasing-subsequence)
+  * `A` [Наименьшая общая супер-последовательность](src/algorithms/sets/shortest-common-supersequence)
+  * `A` [Задача о рюкзаке](src/algorithms/sets/knapsack-problem) — "0/1" и "неограниченный" рюкзаки
+  * `A` [Максимальный под-массив](src/algorithms/sets/maximum-subarray) — метод полного перебора и алгоритм Кадане
+  * `A` [Комбинации сумм](src/algorithms/sets/combination-sum) — нахождение всех комбинаций, сумма каждой из которых равна заданному числу
+* **Алгоритмы работы со строками**
+  * `B` [Расстояние Хэмминга](src/algorithms/string/hamming-distance) — число позиций, в которых соответствующие символы различны
+  * `A` [Расстояние Левенштейна](src/algorithms/string/levenshtein-distance) — метрика, измеряющая разность между двумя последовательностями
+  * `A` [Алгоритм Кнута — Морриса — Пратта](src/algorithms/string/knuth-morris-pratt) — поиск подстроки (сопоставление с шаблоном)
+  * `A` [Z-функция](src/algorithms/string/z-algorithm) — поиск подстроки (сопоставление с шаблоном)
+  * `A` [Алгоритм Рабина — Карпа](src/algorithms/string/rabin-karp) — поиск подстроки
+  * `A` [Наибольшая общая подстрока](src/algorithms/string/longest-common-substring)
+  * `A` [Разборщик регулярных выражений](src/algorithms/string/regular-expression-matching)
+* **Алгоритмы поиска**
+  * `B` [Линейный поиск](src/algorithms/search/linear-search)
+  * `B` [Поиск с перескоком](src/algorithms/search/jump-search) (поиск блоков) — поиск в упорядоченном массиве
+  * `B` [Двоичный поиск](src/algorithms/search/binary-search) — поиск в упорядоченном массиве
+  * `B` [Интерполяционный поиск](src/algorithms/search/interpolation-search) — поиск в равномерно распределённом упорядоченном массиве.
+* **Алгоритмы сортировки**
+  * `B` [Сортировка пузырьком](src/algorithms/sorting/bubble-sort)
+  * `B` [Сортировка выбором](src/algorithms/sorting/selection-sort)
+  * `B` [Сортировка вставками](src/algorithms/sorting/insertion-sort)
+  * `B` [Пирамидальная сортировка (сортировка кучей)](src/algorithms/sorting/heap-sort)
+  * `B` [Сортировка слиянием](src/algorithms/sorting/merge-sort)
+  * `B` [Быстрая сортировка](src/algorithms/sorting/quick-sort) — с использованием дополнительной памяти и без её использования
+  * `B` [Сортировка Шелла](src/algorithms/sorting/shell-sort)
+  * `B` [Сортировка подсчётом](src/algorithms/sorting/counting-sort)
+  * `B` [Поразрядная сортировка](src/algorithms/sorting/radix-sort)
+* **Связный список**
+  * `B` [Прямой обход](src/algorithms/linked-list/traversal)
+  * `B` [Обратный обход](src/algorithms/linked-list/reverse-traversal)
+* **Деревья**
+  * `B` [Поиск в глубину](src/algorithms/tree/depth-first-search)
+  * `B` [Поиск в ширину](src/algorithms/tree/breadth-first-search)
+* **Графы**
+  * `B` [Поиск в глубину](src/algorithms/graph/depth-first-search)
+  * `B` [Поиск в ширину](src/algorithms/graph/breadth-first-search)
+  * `B` [Алгоритм Краскала](src/algorithms/graph/kruskal) — нахождение минимального остовного дерева для взвешенного неориентированного графа
+  * `A` [Алгоритм Дейкстры](src/algorithms/graph/dijkstra) — нахождение кратчайших путей от одной из вершин графа до всех остальных
+  * `A` [Алгоритм Беллмана — Форда](src/algorithms/graph/bellman-ford) — нахождение кратчайших путей от одной из вершин графа до всех остальных
+  * `A` [Алгоритм Флойда — Уоршелла](src/algorithms/graph/floyd-warshall) — нахождение кратчайших расстояний между всеми вершинами графа
+  * `A` [Задача нахождения цикла](src/algorithms/graph/detect-cycle) — для ориентированных и неориентированных графов (на основе поиска в глубину и системы непересекающихся множеств)
+  * `A` [Алгоритм Прима](src/algorithms/graph/prim) — нахождение минимального остовного дерева для взвешенного неориентированного графа
+  * `A` [Топологическая сортировка](src/algorithms/graph/topological-sorting) — на основе поиска в глубину
+  * `A` [Шарниры (разделяющие вершины)](src/algorithms/graph/articulation-points) — алгоритм Тарьяна (на основе поиска в глубину)
+  * `A` [Мосты](src/algorithms/graph/bridges) — на основе поиска в глубину
+  * `A` [Эйлеров путь и Эйлеров цикл](src/algorithms/graph/eulerian-path) — алгоритм Флёри (однократное посещение каждой вершины)
+  * `A` [Гамильтонов цикл](src/algorithms/graph/hamiltonian-cycle) — проходит через каждую вершину графа ровно один раз
+  * `A` [Компоненты сильной связности](src/algorithms/graph/strongly-connected-components) — алгоритм Косарайю
+  * `A` [Задача коммивояжёра](src/algorithms/graph/travelling-salesman) — кратчайший маршрут, проходящий через указанные города с последующим возвратом в исходный город
+* **Криптография**
+  * `B` [Полиноминальный хэш](src/algorithms/cryptography/polynomial-hash) — функция кольцевого хэша, основанная на полиноме
+* **Машинное обучение**
+  * `B` [Нано-нейрон](https://github.com/trekhleb/nano-neuron) — 7 простых JavaScript функций, отображающих способности машины к обучению (прямое и обратное распространение)
+* **Прочие алгоритмы**
+  * `B` [Ханойская башня](src/algorithms/uncategorized/hanoi-tower)
+  * `B` [Поворот квадратной матрицы](src/algorithms/uncategorized/square-matrix-rotation) — используется дополнительная память
+  * `B` [Прыжки](src/algorithms/uncategorized/jump-game) — на основе бэктрекинга, динамического программирования (сверху-вниз + снизу-вверх) и жадных алгоритмов 
+  * `B` [Поиск уникальных путей](src/algorithms/uncategorized/unique-paths) — на основе бэктрекинга, динамического программирования и треугольника Паскаля
+  * `B` [Подсчёт дождевой воды](src/algorithms/uncategorized/rain-terraces) — на основе перебора и динамического программирования
+  * `B` [Задача о рекурсивной лестнице](src/algorithms/uncategorized/recursive-staircase) — подсчёт количества путей, по которым можно достичь верха лестницы (4 способа)
+  * `A` [Задача об N ферзях](src/algorithms/uncategorized/n-queens)
+  * `A` [Маршрут коня](src/algorithms/uncategorized/knight-tour)
+
+### Алгоритмы по парадигме программирования
+
+Парадигма программирования — общий метод или подход, лежащий в основе целого класса алгоритмов. Понятие "парадигма программирования" является более абстрактным по отношению к понятию "алгоритм", которое в свою очередь является более абстрактным по отношению к понятию "компьютерная программа".
+
+* **Алгоритмы полного перебора** — поиск лучшего решения исчерпыванием всевозможных вариантов
+  * `B` [Линейный поиск](src/algorithms/search/linear-search)
+  * `B` [Подсчёт дождевой воды](src/algorithms/uncategorized/rain-terraces)
+  * `B` [Задача о рекурсивной лестнице](src/algorithms/uncategorized/recursive-staircase) — подсчёт количества путей, по которым можно достичь верха лестницы
+  * `A` [Максимальный подмассив](src/algorithms/sets/maximum-subarray)
+  * `A` [Задача коммивояжёра](src/algorithms/graph/travelling-salesman) — кратчайший маршрут, проходящий через указанные города с последующим возвратом в исходный город
+  * `A` [Дискретное преобразование Фурье](src/algorithms/math/fourier-transform) — разложение временной функции (сигнала) на частотные составляющие
+* **Жадные алгоритмы** — принятие локально оптимальных решений с учётом допущения об оптимальности конечного решения 
+  * `B` [Прыжки](src/algorithms/uncategorized/jump-game)
+  * `A` [Задача о неограниченном рюкзаке](src/algorithms/sets/knapsack-problem)
+  * `A` [Алгоритм Дейкстры](src/algorithms/graph/dijkstra) — нахождение кратчайших путей от одной из вершин графа до всех остальных
+  * `A` [Алгоритм Прима](src/algorithms/graph/prim) — нахождение минимального остовного дерева для взвешенного неориентированного графа
+  * `A` [Алгоритм Краскала](src/algorithms/graph/kruskal) — нахождение минимального остовного дерева для взвешенного неориентированного графа
+* **Разделяй и властвуй** — рекурсивное разбиение решаемой задачи на более мелкие
+  * `B` [Двоичный поиск](src/algorithms/search/binary-search)
+  * `B` [Ханойская башня](src/algorithms/uncategorized/hanoi-tower)
+  * `B` [Треугольник Паскаля](src/algorithms/math/pascal-triangle)
+  * `B` [Алгоритм Евклида](src/algorithms/math/euclidean-algorithm) — нахождение наибольшего общего делителя (НОД)
+  * `B` [Сортировка слиянием](src/algorithms/sorting/merge-sort)
+  * `B` [Быстрая сортировка](src/algorithms/sorting/quick-sort)
+  * `B` [Поиск в глубину (дерево)](src/algorithms/tree/depth-first-search)
+  * `B` [Поиск в глубину (граф)](src/algorithms/graph/depth-first-search)
+  * `B` [Прыжки](src/algorithms/uncategorized/jump-game)
+  * `B` [Быстрое возведение в степень](src/algorithms/math/fast-powering)
+  * `A` [Перестановки](src/algorithms/sets/permutations) (с повторениями и без повторений)
+  * `A` [Сочетания](src/algorithms/sets/combinations) (с повторениями и без повторений)
+* **Динамическое программирование** — решение общей задачи конструируется на основе ранее найденных решений подзадач
+  * `B` [Числа Фибоначчи](src/algorithms/math/fibonacci)
+  * `B` [Прыжки](src/algorithms/uncategorized/jump-game)
+  * `B` [Поиск уникальных путей](src/algorithms/uncategorized/unique-paths)
+  * `B` [Подсчёт дождевой воды](src/algorithms/uncategorized/rain-terraces)
+  * `B` [Задача о рекурсивной лестнице](src/algorithms/uncategorized/recursive-staircase) — подсчёт количества путей, по которым можно достичь верха лестницы
+  * `A` [Расстояние Левенштейна](src/algorithms/string/levenshtein-distance) — метрика, измеряющая разность между двумя последовательностями
+  * `A` [Наибольшая общая подпоследовательность](src/algorithms/sets/longest-common-subsequence)
+  * `A` [Наибольшая общая подстрока](src/algorithms/string/longest-common-substring)
+  * `A` [Наибольшая увеличивающаяся подпоследовательность](src/algorithms/sets/longest-increasing-subsequence)
+  * `A` [Наименьшая общая суперпоследовательность](src/algorithms/sets/shortest-common-supersequence)
+  * `A` [Рюкзак 0-1](src/algorithms/sets/knapsack-problem)
+  * `A` [Разбиение числа](src/algorithms/math/integer-partition)
+  * `A` [Максимальный подмассив](src/algorithms/sets/maximum-subarray)
+  * `A` [Алгоритм Беллмана — Форда](src/algorithms/graph/bellman-ford) — поиск кратчайшего пути во взвешенном графе
+  * `A` [Алгоритм Флойда — Уоршелла](src/algorithms/graph/floyd-warshall) — нахождение кратчайших путей от одной из вершин графа до всех остальных
+  * `A` [Разборщик регулярных выражений](src/algorithms/string/regular-expression-matching)
+* **Поиск с возвратом (бэктрекинг)** — при поиске решения многократно делается попытка расширить текущее частичное решение. Если расширение невозможно, то происходит возврат к предыдущему более короткому частичному решению, и делается попытка его расширить другим возможным способом. Обычно используется обход пространства состояний в глубину.
+  * `B` [Прыжки](src/algorithms/uncategorized/jump-game)
+  * `B` [Поиск уникальных путей](src/algorithms/uncategorized/unique-paths)
+  * `B` [Булеан](src/algorithms/sets/power-set) — все подмножества заданного множества
+  * `A` [Гамильтонов цикл](src/algorithms/graph/hamiltonian-cycle) — проходит через каждую вершину графа ровно один раз
+  * `A` [Задача об N ферзях](src/algorithms/uncategorized/n-queens)
+  * `A` [Маршрут коня](src/algorithms/uncategorized/knight-tour)
+  * `A` [Комбинации сумм](src/algorithms/sets/combination-sum) — нахождение всех комбинаций, сумма каждой из которых равна заданному числу
+* **Метод ветвей и границ** — основан на упорядоченном переборе решений и рассмотрении только тех из них, которые являются перспективными (по тем или иным признакам) и отбрасывании бесперспективных множеств решений. Обычно используется обход в ширину в совокупности с обходом дерева пространства состояний в глубину.
+
+## Как использовать этот репозиторий
+
+**Установка всех зависимостей**
+```
+npm install
+```
+
+**Запуск ESLint**
+
+Эта команда может потребоваться вам для проверки качества кода.
+
+```
+npm run lint
+```
+
+**Запуск всех тестов**
+
+```
+npm test
+```
+
+**Запуск определённого теста**
+
+```
+npm test -- 'LinkedList'
+```
+
+**Песочница**
+
+Вы можете экспериментировать с алгоритмами и структурами данных в файле `./src/playground/playground.js` 
+(файл `./src/playground/__test__/playground.test.js` предназначен для написания тестов).
+
+Для проверки работоспособности вашего кода используйте команду:
+
+```
+npm test -- 'playground'
+```
+
+## Полезная информация
+
+### Ссылки
+
+[▶ О структурах данных и алгоритмах](https://www.youtube.com/playlist?list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+
+### Нотация «О» большое
+
+*Нотация «О» большое* используется для классификации алгоритмов в соответствии с ростом времени выполнения и затрачиваемой памяти при увеличении размера входных данных. На диаграмме ниже представлены общие порядки роста алгоритмов в соответствии с нотацией «О» большое.
+
+![Big O graphs](./assets/big-o-graph.png)
+
+Источник: [Big O Cheat Sheet](http://bigocheatsheet.com/).
+
+Ниже представлены часто используемые обозначения в нотации «О» большое, а также сравнение их производительностей на различных размерах входных данных.
+
+| Нотация «О» большое | 10 элементов | 100 элементов | 1000 элементов |
+| ------------------- | ------------ | ------------- | -------------- |
+| **O(1)**            | 1            | 1             | 1              |
+| **O(log N)**        | 3            | 6             | 9              |
+| **O(N)**            | 10           | 100           | 1000           |
+| **O(N log N)**      | 30           | 600           | 9000           |
+| **O(N^2)**          | 100          | 10000         | 1000000        |
+| **O(2^N)**          | 1024         | 1.26e+29      | 1.07e+301      |
+| **O(N!)**           | 3628800      | 9.3e+157      | 4.02e+2567     |
+
+### Сложности операций в структурах данных
+
+| Структура данных           | Получение | Поиск     | Вставка   | Удаление  | Комментарии |
+| -------------------------- | :-------: | :-------: | :-------: | :-------: | :---------- |
+| **Массив**                 | 1         | n         | n         | n         |             |
+| **Стек**                   | n         | n         | 1         | 1         |             |
+| **Очередь**                | n         | n         | 1         | 1         |             |
+| **Связный список**         | n         | n         | 1         | n         |             |
+| **Хеш-таблица**            | -         | n         | n         | n         | Для идеальной хеш-функции — O(1) |
+| **Двоичное дерево поиска** | n         | n         | n         | n         | В сбалансированном дереве — O(log(n)) |
+| **B-дерево**               | log(n)    | log(n)    | log(n)    | log(n)    |           |
+| **Красно-чёрное дерево**   | log(n)    | log(n)    | log(n)    | log(n)    |           |
+| **АВЛ-дерево**             | log(n)    | log(n)    | log(n)    | log(n)    |           |
+| **Фильтр Блума**           | -         | 1         | 1         | -         | Возможно получение ложно-положительного срабатывания |
+
+### Сложности алгоритмов сортировки
+
+| Наименование               | Лучший случай | Средний случай | Худший случай | Память | Устойчивость | Комментарии |
+| -------------------------- | :-----------: | :------------: | :-----------: | :----: | :----------: | :---------- |
+| **Сортировка пузырьком**   | n             | n<sup>2</sup>  | n<sup>2</sup> | 1      | Да           |             |
+| **Сортировка вставками**   | n             | n<sup>2</sup>  | n<sup>2</sup> | 1      | Да           |             |
+| **Сортировка выбором**     | n<sup>2</sup> | n<sup>2</sup>  | n<sup>2</sup> | 1      | Нет          |             |
+| **Сортировка кучей**       | n&nbsp;log(n) | n&nbsp;log(n)  | n&nbsp;log(n) | 1      | Нет          |             |
+| **Сортировка слиянием**    | n&nbsp;log(n) | n&nbsp;log(n)  | n&nbsp;log(n) | n      | Да           |             |
+| **Быстрая сортировка**     | n&nbsp;log(n) | n&nbsp;log(n)  | n<sup>2</sup> | log(n) | Нет          | Быстрая сортировка обычно выполняется с использованием O(log(n)) дополнительной памяти |
+| **Сортировка Шелла**       | n&nbsp;log(n) | зависит от выбранных шагов | n&nbsp;(log(n))<sup>2</sup>  | 1      | Нет          |           |
+| **Сортировка подсчётом**   | n + r         | n + r          | n + r         | n + r  | Да           | r — наибольшее число в массиве |
+| **Поразрядная сортировка** | n * k         | n * k          | n * k         | n + k  | Да           | k — длина самого длинного ключа |

README.tr-TR.md

@@ -0,0 +1,313 @@
+# JavaScript Algoritmalar ve Veri Yapıları
+
+[![CI](https://github.com/trekhleb/javascript-algorithms/workflows/CI/badge.svg)](https://github.com/trekhleb/javascript-algorithms/actions)
+[![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)
+
+Bu repository JavaScript'e ait popüler
+algoritma ve veri yapılarını içermektedir.
+
+Her bir algoritma ve veri yapısı kendine 
+ait açıklama ve videoya sahip README dosyası içerir. 
+
+_Read this in other languages:_
+[_简体中文_](README.zh-CN.md),
+[_繁體中文_](README.zh-TW.md),
+[_한국어_](README.ko-KR.md),
+[_日本語_](README.ja-JP.md),
+[_Polski_](README.pl-PL.md),
+[_Français_](README.fr-FR.md),
+[_Español_](README.es-ES.md),
+[_Português_](README.pt-BR.md),
+[_Русский_](README.ru-RU.md),
+[_Italiana_](README.it-IT.md)
+
+*☝ Not, bu proje araştırma ve öğrenme amacı ile yapılmış 
+olup üretim için **yaplılmamıştır**.*
+
+## Veri Yapıları
+
+Bir veri yapısı, verileri bir bilgisayarda organize etmenin ve depolamanın belirli bir yoludur, böylece
+verimli bir şekilde erişilebilir ve değiştirilebilir. Daha doğrusu, bir veri yapısı bir veri koleksiyonudur,
+aralarındaki ilişkiler, ve işlevler veya işlemler
+veriye uygulanabilir.
+
+`B` - Başlangıç, `A` - İleri Seviye
+
+* `B` [Bağlantılı Veri Yapısı](src/data-structures/linked-list)
+* `B` [Çift Yönlü Bağlı Liste](src/data-structures/doubly-linked-list)
+* `B` [Kuyruk](src/data-structures/queue)
+* `B` [Yığın](src/data-structures/stack)
+* `B` [Hash Table](src/data-structures/hash-table)
+* `B` [Heap](src/data-structures/heap) - max and min heap versions
+* `B` [Öncelikli Kuyruk](src/data-structures/priority-queue)
+* `A` [Trie](src/data-structures/trie)
+* `A` [Ağaç](src/data-structures/tree)
+  * `A` [İkili Arama Ağaçları](src/data-structures/tree/binary-search-tree)
+  * `A` [AVL Tree](src/data-structures/tree/avl-tree)
+  * `A` [Red-Black Tree](src/data-structures/tree/red-black-tree)
+  * `A` [Segment Tree](src/data-structures/tree/segment-tree) - with min/max/sum range queries examples
+  * `A` [Fenwick Tree](src/data-structures/tree/fenwick-tree) (Binary Indexed Tree)
+* `A` [Graph](src/data-structures/graph) (both directed and undirected)
+* `A` [Disjoint Set](src/data-structures/disjoint-set)
+* `A` [Bloom Filter](src/data-structures/bloom-filter)
+
+## Algoritmalar
+
+Bir algoritma, bir problem sınıfının nasıl çözüleceğine dair kesin bir tanımlamadır. Bu
+bir işlem dizisini kesin olarak tanımlayan bir dizi kural.
+
+
+`B` - Başlangıç, `A` - İleri Seviye
+
+### Konusuna göre Algoritma
+
+* **Matematik**
+  * `B` [Bit Manipülasyonu](src/algorithms/math/bits) - set/get/update/clear bits, multiplication/division by two, make negative etc.
+  * `B` [Faktöriyel](src/algorithms/math/factorial) 
+  * `B` [Fibonacci Sayısı](src/algorithms/math/fibonacci) - klasik ve kapalı-form versiyonları
+  * `B` [Asallık Testi](src/algorithms/math/primality-test) (trial division method)
+  * `B` [Öklid Algoritması](src/algorithms/math/euclidean-algorithm) - En büyük ortak bölen hesaplama (EBOB)
+  * `B` [En küçük Ortak Kat](src/algorithms/math/least-common-multiple) (EKOK)
+  * `B` [Sieve of Eratosthenes](src/algorithms/math/sieve-of-eratosthenes) - belirli bir sayıya kadarki asal sayıları bulma
+  * `B` [Is Power of Two](src/algorithms/math/is-power-of-two) - sayı ikinin katı mı sorgusu (naive ve bitwise algoritmaları)
+  * `B` [Paskal Üçgeni](src/algorithms/math/pascal-triangle)
+  * `B` [Karmaşık Sayılar](src/algorithms/math/complex-number) - karmaşık sayılar ve bunlarla temel işlemler
+  * `B` [Radyan & Derece](src/algorithms/math/radian) - radyandan dereceye çeviri ve tersi
+  * `B` [Fast Powering](src/algorithms/math/fast-powering)
+  * `A` [Tamsayı Bölümü](src/algorithms/math/integer-partition)
+  * `A` [Karekök](src/algorithms/math/square-root) - Newton yöntemi
+  * `A` [Liu Hui π Algoritması](src/algorithms/math/liu-hui) - N-gons'a göre yaklaşık π hesabı
+  * `A` [Ayrık Fourier Dönüşümü](src/algorithms/math/fourier-transform) - bir zaman fonksiyonunu (bir sinyal) onu oluşturan frekanslara ayırır
+* **Setler**
+  * `B` [Kartezyen Ürün](src/algorithms/sets/cartesian-product) - product of multiple sets
+  * `B` [Fisher–Yates Shuffle](src/algorithms/sets/fisher-yates) - sonlu bir dizinin rastgele permütasyonu
+  * `A` [Power Set](src/algorithms/sets/power-set) - all subsets of a set (bitwise and backtracking solutions)
+  * `A` [Permütasyonlar](src/algorithms/sets/permutations)(tekrarlı ve tekrarsız)
+  * `A` [Kombinasyonlar](src/algorithms/sets/combinations) (tekrarlı ve tekrarsız)
+  * `A` [En Uzun Ortak Altdizi](src/algorithms/sets/longest-common-subsequence) (LCS)
+  * `A` [En Uzun Artan Altdizi](src/algorithms/sets/longest-increasing-subsequence)
+  * `A` [En Kısa Ortak Üst Sıra](src/algorithms/sets/shortest-common-supersequence) (SCS)
+  * `A` [Knapsack Problem](src/algorithms/sets/knapsack-problem) - "0/1" and "Unbound" ones
+  * `A` [Maksimum Altdizi](src/algorithms/sets/maximum-subarray) - "Brute Force" ve "Dinamik Programlara" (Kadane'nin) versiyonu
+  * `A` [Kombinasyon Toplamı](src/algorithms/sets/combination-sum) - belirli toplamı oluşturan tüm kombinasyonları bulun
+* **Metin**
+  * `B` [Hamming Mesafesi](src/algorithms/string/hamming-distance) - sembollerin farklı olduğu konumların sayısı
+  * `A` [Levenshtein Mesafesi](src/algorithms/string/levenshtein-distance) - iki sekans arasındaki minimum düzenleme mesafesi
+  * `A` [Knuth–Morris–Pratt Algoritması](src/algorithms/string/knuth-morris-pratt) (KMP Algorithm) - substring search (pattern matching)
+  * `A` [Z Algoritması](src/algorithms/string/z-algorithm) - altmetin araması (desen eşleştirme)
+  * `A` [Rabin Karp Algoritması](src/algorithms/string/rabin-karp) - altmetin araması
+  * `A` [En Uzun Ortak Alt Metin](src/algorithms/string/longest-common-substring)
+  * `A` [Regular Expression Eşleme](src/algorithms/string/regular-expression-matching)
+* **Aramalar**
+  * `B` [Doğrusal Arama](src/algorithms/search/linear-search)
+  * `B` [Jump Search](src/algorithms/search/jump-search) (ya da Block Search) - sıralı dizide ara
+  * `B` [İkili Arama](src/algorithms/search/binary-search) - sıralı dizide ara
+  * `B` [Interpolation Search](src/algorithms/search/interpolation-search) - tekdüze dağıtılmış sıralı dizide arama
+* **Sıralama**
+  * `B` [Bubble Sort](src/algorithms/sorting/bubble-sort)
+  * `B` [Selection Sort](src/algorithms/sorting/selection-sort)
+  * `B` [Insertion Sort](src/algorithms/sorting/insertion-sort)
+  * `B` [Heap Sort](src/algorithms/sorting/heap-sort)
+  * `B` [Merge Sort](src/algorithms/sorting/merge-sort)
+  * `B` [Quicksort](src/algorithms/sorting/quick-sort) - in-place and non-in-place implementations
+  * `B` [Shellsort](src/algorithms/sorting/shell-sort)
+  * `B` [Counting Sort](src/algorithms/sorting/counting-sort)
+  * `B` [Radix Sort](src/algorithms/sorting/radix-sort)
+* **Bağlantılı Liste**
+  * `B` [Straight Traversal](src/algorithms/linked-list/traversal)
+  * `B` [Reverse Traversal](src/algorithms/linked-list/reverse-traversal)
+* **Ağaçlar**
+  * `B` [Depth-First Search](src/algorithms/tree/depth-first-search) (DFS)
+  * `B` [Breadth-First Search](src/algorithms/tree/breadth-first-search) (BFS)
+* **Graphs**
+  * `B` [Depth-First Search](src/algorithms/graph/depth-first-search) (DFS)
+  * `B` [Breadth-First Search](src/algorithms/graph/breadth-first-search) (BFS)
+  * `B` [Kruskal’s Algorithm](src/algorithms/graph/kruskal) - ağırlıklı yönlendirilmemiş grafik için Minimum Yayılma Ağacı'nı (MST) bulma
+  * `A` [Dijkstra Algorithm](src/algorithms/graph/dijkstra) - tek tepe noktasından tüm grafik köşelerine en kısa yolları bulmak
+  * `A` [Bellman-Ford Algorithm](src/algorithms/graph/bellman-ford) - tek tepe noktasından tüm grafik köşelerine en kısa yolları bulmak
+  * `A` [Floyd-Warshall Algorithm](src/algorithms/graph/floyd-warshall) - tüm köşe çiftleri arasındaki en kısa yolları bulun
+  * `A` [Detect Cycle](src/algorithms/graph/detect-cycle) - hem yönlendirilmiş hem de yönlendirilmemiş grafikler için (DFS ve Ayrık Küme tabanlı sürümler)
+  * `A` [Prim’s Algorithm](src/algorithms/graph/prim) - ağırlıklı yönlendirilmemiş grafik için Minimum Yayılma Ağacı'nı (MST) bulma
+  * `A` [Topological Sorting](src/algorithms/graph/topological-sorting) - DFS metodu
+  * `A` [Articulation Points](src/algorithms/graph/articulation-points) - Tarjan's algoritması (DFS based)
+  * `A` [Bridges](src/algorithms/graph/bridges) - DFS yöntemi ile algoritma
+  * `A` [Eulerian Path and Eulerian Circuit](src/algorithms/graph/eulerian-path) - Fleury'nin algoritması - Her kenara tam olarak bir kez ulaş
+  * `A` [Hamiltonian Cycle](src/algorithms/graph/hamiltonian-cycle) - Her köşeyi tam olarak bir kez ziyaret et
+  * `A` [Strongly Connected Components](src/algorithms/graph/strongly-connected-components) - Kosaraju's algorithm
+  * `A` [Travelling Salesman Problem](src/algorithms/graph/travelling-salesman) - her şehri ziyaret eden ve başlangıç ​​şehrine geri dönen mümkün olan en kısa rota
+* **Kriptografi**
+  * `B` [Polynomial Hash](src/algorithms/cryptography/polynomial-hash) - polinom temelinde dönen hash işlevi
+  * `B` [Caesar Cipher](src/algorithms/cryptography/caesar-cipher) - simple substitution cipher
+* **Makine Öğrenmesi**
+  * `B` [NanoNeuron](https://github.com/trekhleb/nano-neuron) - 7 simple JS functions that illustrate how machines can actually learn (forward/backward propagation)
+* **Kategoriye Ayrılmayanlar**
+  * `B` [Tower of Hanoi](src/algorithms/uncategorized/hanoi-tower)
+  * `B` [Square Matrix Rotation](src/algorithms/uncategorized/square-matrix-rotation) - in-place algorithm
+  * `B` [Jump Game](src/algorithms/uncategorized/jump-game) - backtracking, dynamic programming (top-down + bottom-up) and greedy examples 
+  * `B` [Unique Paths](src/algorithms/uncategorized/unique-paths) - backtracking, dynamic programming and Pascal's Triangle based examples 
+  * `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - trapping rain water problem (dynamic programming and brute force versions)
+  * `B` [Recursive Staircase](src/algorithms/uncategorized/recursive-staircase) - tepeye ulaşmanın yollarını sayma (4 çözüm)
+  * `A` [N-Queens Problem](src/algorithms/uncategorized/n-queens)
+  * `A` [Knight's Tour](src/algorithms/uncategorized/knight-tour)
+
+### Algoritmik Paradigma
+
+Algoritmik paradigma, bir sınıfın tasarımının altında yatan genel bir yöntem veya yaklaşımdır. 
+Algoritma dizayn tekniği olarak düşünülebilir. Her bir altproblemi (subproblem) asıl problemle 
+benzerlik gösteren problemlere uygulanabilir.
+
+* **Brute Force** - mümkün olan tüm çözümleri tara ve en iyisini seç
+  * `B` [Doğrusal Arama](src/algorithms/search/linear-search)
+  * `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - trapping rain water problem
+  * `B` [Recursive Staircase](src/algorithms/uncategorized/recursive-staircase) - tepeye çıkmanın yollarını hesapla
+  * `A` [Maximum Subarray](src/algorithms/sets/maximum-subarray)
+  * `A` [Travelling Salesman Problem](src/algorithms/graph/travelling-salesman) - her şehri ziyaret eden ve başlangıç şehrine geri dönen mümkün olan en kısa rota
+  * `A` [Discrete Fourier Transform](src/algorithms/math/fourier-transform) - bir zaman fonksiyonunu (bir sinyal) onu oluşturan frekanslara ayırır
+* **Açgözlü** - geleceği düşünmeden şu an için en iyi seçeneği seçin
+  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
+  * `A` [Unbound Knapsack Problem](src/algorithms/sets/knapsack-problem)
+  * `A` [Dijkstra Algorithm](src/algorithms/graph/dijkstra) - tüm grafik köşelerine giden en kısa yolu bulmak
+  * `A` [Prim’s Algorithm](src/algorithms/graph/prim) - ağırlıklı yönlendirilmemiş grafik için Minimum Yayılma Ağacı'nı (MST) bulma
+  * `A` [Kruskal’s Algorithm](src/algorithms/graph/kruskal) - ağırlıklı yönlendirilmemiş grafik için Minimum Yayılma Ağacı'nı (MST) bulma
+* **Böl ve Fethet** - sorunu daha küçük parçalara bölün ve sonra bu parçaları çözün
+  * `B` [Binary Search](src/algorithms/search/binary-search)
+  * `B` [Tower of Hanoi](src/algorithms/uncategorized/hanoi-tower)
+  * `B` [Pascal's Triangle](src/algorithms/math/pascal-triangle)
+  * `B` [Euclidean Algorithm](src/algorithms/math/euclidean-algorithm) - calculate the Greatest Common Divisor (GCD)
+  * `B` [Merge Sort](src/algorithms/sorting/merge-sort)
+  * `B` [Quicksort](src/algorithms/sorting/quick-sort)
+  * `B` [Tree Depth-First Search](src/algorithms/tree/depth-first-search) (DFS)
+  * `B` [Graph Depth-First Search](src/algorithms/graph/depth-first-search) (DFS)
+  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
+  * `B` [Fast Powering](src/algorithms/math/fast-powering)
+  * `A` [Permutations](src/algorithms/sets/permutations) (tekrarlı ve tekrarsız)
+  * `A` [Combinations](src/algorithms/sets/combinations) (tekrarlı ve tekrarsız)
+* **Dinamik Programlama** - önceden bulunan alt çözümleri kullanarak bir çözüm oluşturmak
+  * `B` [Fibonacci Sayısı](src/algorithms/math/fibonacci)
+  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
+  * `B` [Eşsiz Yol](src/algorithms/uncategorized/unique-paths)
+  * `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - trapping rain water problem
+  * `B` [Recursive Staircase](src/algorithms/uncategorized/recursive-staircase) - zirveye ulaşmanın yollarının sayısını sayın
+  * `A` [Levenshtein Distance](src/algorithms/string/levenshtein-distance) - iki sekans arasındaki minimum düzenleme mesafesi
+  * `A` [Longest Common Subsequence](src/algorithms/sets/longest-common-subsequence) (LCS)
+  * `A` [Longest Common Substring](src/algorithms/string/longest-common-substring)
+  * `A` [Longest Increasing Subsequence](src/algorithms/sets/longest-increasing-subsequence)
+  * `A` [Shortest Common Supersequence](src/algorithms/sets/shortest-common-supersequence)
+  * `A` [0/1 Knapsack Problem](src/algorithms/sets/knapsack-problem)
+  * `A` [Integer Partition](src/algorithms/math/integer-partition)
+  * `A` [Maximum Subarray](src/algorithms/sets/maximum-subarray)
+  * `A` [Bellman-Ford Algorithm](src/algorithms/graph/bellman-ford) - tüm grafik köşelerine giden en kısa yolu bulmak
+  * `A` [Floyd-Warshall Algorithm](src/algorithms/graph/floyd-warshall) - tüm köşe çiftleri arasındaki en kısa yolları bulun
+  * `A` [Regular Expression Matching](src/algorithms/string/regular-expression-matching) 
+* **Backtracking** - brute forceye benzer, mümkün tüm sonuçları tara, ancak bir sonraki çözümü her ürettiğinizde test edersiniz
+tüm koşulları karşılıyorsa ve ancak o zaman sonraki çözümleri üretmeye devam edin. Aksi takdirde, geri dönün ve farklı bir çözüm arayın(?).
+Normally the DFS traversal of state-space is being used.
+  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
+  * `B` [Unique Paths](src/algorithms/uncategorized/unique-paths)
+  * `B` [Power Set](src/algorithms/sets/power-set) - all subsets of a set
+  * `A` [Hamiltonian Cycle](src/algorithms/graph/hamiltonian-cycle) - Her köşeyi tam olarak bir kez ziyaret edin
+  * `A` [N-Queens Problem](src/algorithms/uncategorized/n-queens)
+  * `A` [Knight's Tour](src/algorithms/uncategorized/knight-tour)
+  * `A` [Combination Sum](src/algorithms/sets/combination-sum) - belirli toplamı oluşturan tüm kombinasyonları bulun
+* **Branch & Bound** - remember the lowest-cost solution found at each stage of the backtracking
+search, and use the cost of the lowest-cost solution found so far as a lower bound on the cost of
+a least-cost solution to the problem, in order to discard partial solutions with costs larger than the
+lowest-cost solution found so far. Normally BFS traversal in combination with DFS traversal of state-space
+tree is being used.
+
+## Repository'in Kullanımı
+
+**Bütün dependencyleri kurun**
+```
+npm install
+```
+
+**ESLint'i başlatın**
+
+Bunu kodun kalitesini kontrol etmek amacı ile çalıştırabilirsin.
+
+```
+npm run lint
+```
+
+**Bütün testleri çalıştır**
+```
+npm test
+```
+
+**Testleri ismine göre çalıştır**
+```
+npm test -- 'LinkedList'
+```
+
+**Deneme Alanı**
+
+data-structures ve algorithms içerisinde `./src/playground/playground.js` 
+yazarak `./src/playground/__test__/playground.test.js` için test edebilirsin.
+
+
+Ardından basitçe alttaki komutu girerek kodunun beklendiği gibi çalışıp çalışmadığını test edebilirsin:
+
+```
+npm test -- 'playground'
+```
+
+## Yararlı Bilgiler
+
+### Referanslar
+
+[▶ Data Structures and Algorithms on YouTube](https://www.youtube.com/playlist?list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+
+### Big O Notation
+
+* Big O notation *, algoritmaları, giriş boyutu büyüdükçe çalışma süresi veya alan gereksinimlerinin nasıl arttığına göre sınıflandırmak için kullanılır.
+Aşağıdaki grafikte, Big O gösteriminde belirtilen algoritmaların en yaygın büyüme sıralarını bulabilirsiniz.
+
+![Big O graphs](./assets/big-o-graph.png)
+
+Kaynak: [Big O Cheat Sheet](http://bigocheatsheet.com/).
+
+Altta Big O notations ve farklı input boyutlarına karşın yapılmış performans karşılaştırması listelenmektedir.
+
+| Big O Notation | 10 Element için hesaplama | 100 Element için hesaplama | 1000 Element için hesaplama  |
+| -------------- | ---------------------------- | ----------------------------- | ------------------------------- |
+| **O(1)**       | 1                            | 1                             | 1                               |
+| **O(log N)**   | 3                            | 6                             | 9                               |
+| **O(N)**       | 10                           | 100                           | 1000                            |
+| **O(N log N)** | 30                           | 600                           | 9000                            |
+| **O(N^2)**     | 100                          | 10000                         | 1000000                         |
+| **O(2^N)**     | 1024                         | 1.26e+29                      | 1.07e+301                       |
+| **O(N!)**      | 3628800                      | 9.3e+157                      | 4.02e+2567                      |
+
+### Veri Yapısı İşlem Karmaşıklığı
+
+| Veri Yapısı          | Access    | Search    | Insertion | Deletion  | Comments  |
+| ----------------------- | :-------: | :-------: | :-------: | :-------: | :-------- |
+| **Dizi**               | 1         | n         | n         | n         |           |
+| **Yığın**               | n         | n         | 1         | 1         |           |
+| **Sıralı**               | n         | n         | 1         | 1         |           |
+| **Bağlantılı Liste**         | n         | n         | 1         | n         |           |
+| **Yığın Tablo**          | -         | n         | n         | n         | Kusursuz hash fonksiyonu durumunda sonuç O(1) |
+| **İkili Arama Ağacı**  | n         | n         | n         | n         | In case of balanced tree costs would be O(log(n)) |
+| **B-Tree**              | log(n)    | log(n)    | log(n)    | log(n)    |           |
+| **Red-Black Tree**      | log(n)    | log(n)    | log(n)    | log(n)    |           |
+| **AVL Tree**            | log(n)    | log(n)    | log(n)    | log(n)    |           |
+| **Bloom Filter**        | -         | 1         | 1         | -         | Arama esnasında yanlış sonuçlar çıkabilir |
+
+### Dizi Sıralama Algoritmaları Karmaşıklığı
+
+| İsim                  | En İyi            | Ortalama             | En Kötü               | Hafıza    | Kararlı    | Yorumlar  |
+| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
+| **Bubble sort**       | n               | n<sup>2</sup>       | n<sup>2</sup>       | 1         | Evet       |           |
+| **Insertion sort**    | n               | n<sup>2</sup>       | n<sup>2</sup>       | 1         | Evet       |           |
+| **Selection sort**    | n<sup>2</sup>   | n<sup>2</sup>       | n<sup>2</sup>       | 1         | Hayır        |           |
+| **Heap sort**         | n&nbsp;log(n)   | n&nbsp;log(n)       | n&nbsp;log(n)       | 1         | Hayır        |           |
+| **Merge sort**        | n&nbsp;log(n)   | n&nbsp;log(n)       | n&nbsp;log(n)       | n         | Evet       |           |
+| **Quick sort**        | n&nbsp;log(n)   | n&nbsp;log(n)       | n<sup>2</sup>       | log(n)    | Hayır        | Hızlı sıralama genellikle O(log(n)) yığın alanıyla yapılır |
+| **Shell sort**        | n&nbsp;log(n)   | depends on gap sequence   | n&nbsp;(log(n))<sup>2</sup>  | 1         | Hayır         |           |
+| **Counting sort**     | n + r           | n + r               | n + r               | n + r     | Evet       | r - dizideki en büyük sayı |
+| **Radix sort**        | n * k           | n * k               | n * k               | n + k     | Evet       | k - en uzun key'in uzunluğu |
+
+## Projeyi Destekleme
+
+Bu projeyi buradan destekleyebilirsiniz ❤️️ [GitHub](https://github.com/sponsors/trekhleb) veya ❤️️ [Patreon](https://www.patreon.com/trekhleb).          

README.zh-CN.md

@@ -1,6 +1,6 @@
 # JavaScript 算法与数据结构
 
-[![build status](https://travis-ci.org/trekhleb/javascript-algorithms.svg?branch=master)](https://travis-ci.org/trekhleb/javascript-algorithms)
+[![CI](https://github.com/trekhleb/javascript-algorithms/workflows/CI/badge.svg)](https://github.com/trekhleb/javascript-algorithms/actions)
 [![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)
 
 本仓库包含了多种基于 JavaScript 的算法与数据结构。
@@ -15,7 +15,10 @@ _Read this in other languages:_
 [_Polski_](README.pl-PL.md),
 [_Français_](README.fr-FR.md),
 [_Español_](README.es-ES.md),
-[_Português_](README.pt-BR.md)
+[_Português_](README.pt-BR.md),
+[_Русский_](README.ru-RU.md),
+[_Türk_](README.tr-TR.md),
+[_Italiana_](README.it-IT.md)
 
 *注意：这个项目仅用于学习和研究，**不是**用于生产环境。*
 
@@ -225,7 +228,7 @@ npm test -- 'LinkedList'
 
 你可以在 `./src/playground/playground.js` 文件中操作数据结构与算法，并在 `./src/playground/__test__/playground.test.js` 中编写测试。
 
-然后，只需运行以下命令来测试你的 Playground 是否按无误:
+然后，只需运行以下命令来测试你的 Playground 是否无误:
 
 ```
 npm test -- 'playground'

README.zh-TW.md

@@ -1,6 +1,6 @@
 # JavaScript 演算法與資料結構
 
-[![build status](https://travis-ci.org/trekhleb/javascript-algorithms.svg?branch=master)](https://travis-ci.org/trekhleb/javascript-algorithms)
+[![CI](https://github.com/trekhleb/javascript-algorithms/workflows/CI/badge.svg)](https://github.com/trekhleb/javascript-algorithms/actions)
 [![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)
 
 這個知識庫包含許多 JavaScript 的資料結構與演算法的基礎範例。
@@ -14,7 +14,10 @@ _Read this in other languages:_
 [_Polski_](README.pl-PL.md),
 [_Français_](README.fr-FR.md),
 [_Español_](README.es-ES.md),
-[_Português_](README.pt-BR.md)
+[_Português_](README.pt-BR.md),
+[_Русский_](README.ru-RU.md),
+[_Türk_](README.tr-TR.md),
+[_Italiana_](README.it-IT.md)
 
 ## 資料結構
 

jest.config.js

@@ -25,4 +25,14 @@ module.exports = {
   // It is reflected in properties such as location.href.
   // @see: https://github.com/facebook/jest/issues/6769
   testURL: 'http://localhost/',
+
+  // @see: https://jestjs.io/docs/en/configuration#coveragethreshold-object
+  coverageThreshold: {
+    global: {
+      statements: 100,
+      branches: 95,
+      functions: 100,
+      lines: 100,
+    },
+  },
 };

package.json

@@ -4,9 +4,10 @@
   "description": "Algorithms and data-structures implemented on JavaScript",
   "main": "index.js",
   "scripts": {
-    "lint": "eslint ./src/*",
+    "lint": "eslint ./src/**",
     "test": "jest",
-    "ci": "npm run lint && npm run test -- --coverage"
+    "coverage": "npm run test -- --coverage",
+    "ci": "npm run lint && npm run coverage"
   },
   "repository": {
     "type": "git",
@@ -33,17 +34,17 @@
   },
   "homepage": "https://github.com/trekhleb/javascript-algorithms#readme",
   "devDependencies": {
-    "@babel/cli": "^7.10.5",
-    "@babel/preset-env": "^7.10.4",
-    "@types/jest": "^26.0.7",
-    "eslint": "^7.5.0",
-    "eslint-config-airbnb": "^18.2.0",
-    "eslint-plugin-import": "^2.22.0",
-    "eslint-plugin-jest": "^23.18.2",
-    "eslint-plugin-jsx-a11y": "^6.3.1",
-    "eslint-plugin-react": "^7.20.3",
-    "husky": "^4.2.5",
-    "jest": "^26.1.0"
+    "@babel/cli": "^7.12.8",
+    "@babel/preset-env": "^7.12.7",
+    "@types/jest": "^26.0.16",
+    "eslint": "^7.14.0",
+    "eslint-config-airbnb": "^18.2.1",
+    "eslint-plugin-import": "^2.22.1",
+    "eslint-plugin-jest": "^24.1.3",
+    "eslint-plugin-jsx-a11y": "^6.4.1",
+    "eslint-plugin-react": "^7.21.5",
+    "husky": "^4.3.0",
+    "jest": "^26.6.3"
   },
   "dependencies": {}
 }

src/algorithms/math/bits/README.fr-FR.md

@@ -0,0 +1,295 @@
+# Manipulation de bits
+
+_Read this in other languages:_
+[english](README.md).
+
+#### Vérifier un bit (_get_)
+
+Cette méthode décale le bit correspondant (_bit shifting_) à la position zéro.
+Ensuite, nous exécutons l'opération `AND` avec un masque comme `0001`.
+Cela efface tous les bits du nombre original sauf le correspondant.
+Si le bit pertinent est `1`, le résultat est `1`, sinon le résultat est `0`.
+
+> Voir [getBit.js](getBit.js) pour plus de détails.
+
+#### Mettre un bit à 1(_set_)
+
+Cette méthode met un bit à `1` en fonction d'un rang (`bitPosition`),
+créant ainsi une valeur qui ressemble à `00100`.
+Ensuite, nous effectuons l'opération `OU` qui met un bit spécifique
+en `1` sans affecter les autres bits du nombre.
+
+> Voir [setBit.js](setBit.js) pour plus de détails.
+
+#### Mettre un bit à 0 (_clear_)
+
+Cette méthode met un bit à `1` en fonction d'un rang (`bitPosition`),
+créant ainsi une valeur qui ressemble à `00100`.
+Puis on inverse ce masque de bits pour obtenir un nombre ressemblant à `11011`.
+Enfin, l'opération `AND` est appliquée au nombre et au masque.
+Cette opération annule le bit.
+
+> Voir [clearBit.js](clearBit.js) pour plus de détails.
+
+#### Mettre à jour un Bit (_update_)
+
+Cette méthode est une combinaison de l'"annulation de bit"
+et du "forçage de bit".
+
+> Voir [updateBit.js](updateBit.js) pour plus de détails.
+
+#### Vérifier si un nombre est pair (_isEven_)
+
+Cette méthode détermine si un nombre donné est pair.
+Elle s'appuie sur le fait que les nombres impairs ont leur dernier
+bit droit à `1`.
+
+```text
+Nombre: 5 = 0b0101
+isEven: false
+
+Nombre: 4 = 0b0100
+isEven: true
+```
+
+> Voir [isEven.js](isEven.js) pour plus de détails.
+
+#### Vérifier si un nombre est positif (_isPositive_)
+
+Cette méthode détermine un le nombre donné est positif.
+Elle s'appuie sur le fait que tous les nombres positifs
+ont leur bit le plus à gauche à `0`.
+Cependant, si le nombre fourni est zéro
+ou zéro négatif, il doit toujours renvoyer `false`.
+
+```text
+Nombre: 1 = 0b0001
+isPositive: true
+
+Nombre: -1 = -0b0001
+isPositive: false
+```
+
+> Voir [isPositive.js](isPositive.js) pour plus de détails.
+
+#### Multiplier par deux
+
+Cette méthode décale un nombre donné d'un bit vers la gauche.
+Ainsi, toutes les composantes du nombre binaire (en puissances de deux) sont
+multipliées par deux et donc le nombre lui-même est
+multiplié par deux.
+
+```
+Avant le décalage
+Nombre: 0b0101 = 5
+Puissances de deux: 0 + 2^2 + 0 + 2^0
+
+Après le décalage
+Nombre: 0b1010 = 10
+Puissances de deux: 2^3 + 0 + 2^1 + 0
+```
+
+> Voir [multiplyByTwo.js](multiplyByTwo.js) pour plus de détails.
+
+#### Diviser par deux
+
+Cette méthode décale un nombre donné d'un bit vers la droite.
+Ainsi, toutes les composantes du nombre binaire (en puissances de deux) sont
+divisées par deux et donc le nombre lui-même est
+divisé par deux, sans reste.
+
+```
+Avant le décalage
+Nombre: 0b0101 = 5
+Puissances de deux: 0 + 2^2 + 0 + 2^0
+
+Après le décalage
+Nombre: 0b0010 = 2
+Puissances de deux: 0 + 0 + 2^1 + 0
+```
+
+> Voir [divideByTwo.js](divideByTwo.js) pour plus de détails.
+
+#### Inverser le signe (_Switch Sign_)
+
+Cette méthode rend positifs les nombres négatifs, et vice-versa.
+Pour ce faire, elle s'appuie sur l'approche "Complément à deux",
+qui inverse tous les bits du nombre et y ajoute 1.
+
+```
+1101 -3
+1110 -2
+1111 -1
+0000  0
+0001  1
+0010  2
+0011  3
+```
+
+> Voir [switchSign.js](switchSign.js) pour plus de détails.
+
+#### Multiplier deux nombres signés
+
+Cette méthode multiplie deux nombres entiers signés
+à l'aide d'opérateurs bit à bit.
+Cette méthode est basée sur les faits suivants:
+
+```text
+a * b peut être écrit sous les formes suivantes:
+  0                     si a est zero ou b est zero ou les deux sont zero
+  2a * (b/2)            si b est pair
+  2a * (b - 1)/2 + a    si b est impair et positif
+  2a * (b + 1)/2 - a    si b est impair et negatif
+```
+
+L'avantage de cette approche est qu'à chaque étape de la récursion
+l'un des opérandes est réduit à la moitié de sa valeur d'origine.
+Par conséquent, la complexité d'exécution est `O(log(b))`
+où `b` est l'opérande qui se réduit de moitié à chaque récursion.
+
+> Voir [multiply.js](multiply.js) pour plus de détails.
+
+#### Multiplier deux nombres positifs
+
+Cette méthode multiplie deux nombres entiers à l'aide d'opérateurs bit à bit.
+Cette méthode s'appuie sur le fait que "Chaque nombre peut être lu
+comme une somme de puissances de 2".
+
+L'idée principale de la multiplication bit à bit
+est que chaque nombre peut être divisé en somme des puissances de deux:
+
+Ainsi
+
+```text
+19 = 2^4 + 2^1 + 2^0
+```
+
+Donc multiplier `x` par `19` est equivalent à :
+
+```text
+x * 19 = x * 2^4 + x * 2^1 + x * 2^0
+```
+
+Nous devons maintenant nous rappeler que `x * 2 ^ 4` équivaut
+à déplacer`x` vers la gauche par `4` bits (`x << 4`).
+
+> Voir [multiplyUnsigned.js](multiplyUnsigned.js) pour plus de détails.
+
+#### Compter les bits à 1
+
+This method counts the number of set bits in a number using bitwise operators.
+The main idea is that we shift the number right by one bit at a time and check
+the result of `&` operation that is `1` if bit is set and `0` otherwise.
+
+Cette méthode décompte les bits à `1` d'un nombre
+à l'aide d'opérateurs bit à bit.
+L'idée principale est de décaler le nombre vers la droite, un bit à la fois,
+et de vérifier le résultat de l'opération `&` :
+`1` si le bit est défini et `0` dans le cas contraire.
+
+```text
+Nombre: 5 = 0b0101
+Décompte des bits à 1 = 2
+```
+
+> Voir [countSetBits.js](countSetBits.js) pour plus de détails.
+
+#### Compter les bits nécessaire pour remplacer un nombre
+
+This methods outputs the number of bits required to convert one number to another.
+This makes use of property that when numbers are `XOR`-ed the result will be number
+of different bits.
+
+Cette méthode retourne le nombre de bits requis
+pour convertir un nombre en un autre.
+Elle repose sur la propriété suivante:
+lorsque les nombres sont évalués via `XOR`, le résultat est le nombre
+de bits différents entre les deux.
+
+```
+5 = 0b0101
+1 = 0b0001
+Nombre de bits pour le remplacement: 1
+```
+
+> Voir [bitsDiff.js](bitsDiff.js) pour plus de détails.
+
+#### Calculer les bits significatifs d'un nombre
+
+Pour connaître les bits significatifs d'un nombre,
+on peut décaler `1` d'un bit à gauche plusieurs fois d'affilée
+jusqu'à ce que ce nombre soit plus grand que le nombre à comparer.
+
+```
+5 = 0b0101
+Décompte des bits significatifs: 3
+On décale 1 quatre fois pour dépasser 5.
+```
+
+> Voir [bitLength.js](bitLength.js) pour plus de détails.
+
+#### Vérifier si un nombre est une puissance de 2
+
+Cette méthode vérifie si un nombre donné est une puissance de deux.
+Elle s'appuie sur la propriété suivante.
+Disons que `powerNumber` est une puissance de deux (c'est-à-dire 2, 4, 8, 16 etc.).
+Si nous faisons l'opération `&` entre `powerNumber` et `powerNumber - 1`,
+elle retournera`0` (dans le cas où le nombre est une puissance de deux).
+
+```
+Nombre: 4 = 0b0100
+Nombre: 3 = (4 - 1) = 0b0011
+4 & 3 = 0b0100 & 0b0011 = 0b0000 <-- Égal à zéro, car c'est une puissance de 2.
+
+Nombre: 10 = 0b01010
+Nombre: 9 = (10 - 1) = 0b01001
+10 & 9 = 0b01010 & 0b01001 = 0b01000 <-- Différent de 0, donc n'est pas une puissance de 2.
+```
+
+> Voir [isPowerOfTwo.js](isPowerOfTwo.js) pour plus de détails.
+
+#### Additionneur complet
+
+Cette méthode ajoute deux nombres entiers à l'aide d'opérateurs bit à bit.
+
+Elle implémente un [additionneur](https://fr.wikipedia.org/wiki/Additionneur)
+simulant un circuit électronique logique,
+pour additionner deux entiers de 32 bits,
+sous la forme « complément à deux ».
+Elle utilise la logique booléenne pour couvrir tous les cas possibles
+d'ajout de deux bits donnés:
+avec et sans retenue de l'ajout de l'étape précédente la moins significative.
+
+Légende:
+
+- `A`: Nombre `A`
+- `B`: Nombre `B`
+- `ai`: ième bit du nombre `A`
+- `bi`: ième bit du nombre `B`
+- `carryIn`: un bit retenu de la précédente étape la moins significative
+- `carryOut`: un bit retenu pour la prochaine étape la plus significative
+- `bitSum`: La somme de `ai`, `bi`, et `carryIn`
+- `resultBin`: Le résultat complet de l'ajout de l'étape actuelle avec toutes les étapes moins significatives (en binaire)
+- `resultDec`: Le résultat complet de l'ajout de l'étape actuelle avec toutes les étapes moins significatives (en decimal)
+
+```
+A = 3: 011
+B = 6: 110
+┌──────┬────┬────┬─────────┬──────────┬─────────┬───────────┬───────────┐
+│  bit │ ai │ bi │ carryIn │ carryOut │  bitSum │ resultBin │ resultDec │
+├──────┼────┼────┼─────────┼──────────┼─────────┼───────────┼───────────┤
+│   0  │ 1  │ 0  │    0    │    0     │     1   │       1   │     1     │
+│   1  │ 1  │ 1  │    0    │    1     │     0   │      01   │     1     │
+│   2  │ 0  │ 1  │    1    │    1     │     0   │     001   │     1     │
+│   3  │ 0  │ 0  │    1    │    0     │     1   │    1001   │     9     │
+└──────┴────┴────┴─────────┴──────────┴─────────┴───────────┴───────────┘
+```
+
+> Voir [fullAdder.js](fullAdder.js) pour plus de détails.  
+> Voir [Full Adder on YouTube](https://www.youtube.com/watch?v=wvJc9CZcvBc&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8).
+
+## Références
+
+- [Bit Manipulation on YouTube](https://www.youtube.com/watch?v=NLKQEOgBAnw&t=0s&index=28&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+- [Negative Numbers in binary on YouTube](https://www.youtube.com/watch?v=4qH4unVtJkE&t=0s&index=30&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+- [Bit Hacks on stanford.edu](https://graphics.stanford.edu/~seander/bithacks.html)

src/algorithms/math/bits/README.md

@@ -1,10 +1,13 @@
 # Bit Manipulation
 
+_Read this in other languages:_
+[français](README.fr-FR.md).
+
 #### Get Bit
 
 This method shifts the relevant bit to the zeroth position.
 Then we perform `AND` operation with one which has bit
-pattern like `0001`.  This clears all bits from the original
+pattern like `0001`. This clears all bits from the original
 number except the relevant one. If the relevant bit is one,
 the result is `1`, otherwise the result is `0`.
 
@@ -53,7 +56,7 @@ isEven: true
 
 #### isPositive
 
-This method determines if the number is positive. It is based on the fact that all positive 
+This method determines if the number is positive. It is based on the fact that all positive
 numbers have their leftmost bit to be set to `0`. However, if the number provided is zero
 or negative zero, it should still return `false`.
 
@@ -230,12 +233,13 @@ Number: 9 = (10 - 1) = 0b01001
 
 This method adds up two integer numbers using bitwise operators.
 
-It implements [full adder](https://en.wikipedia.org/wiki/Adder_(electronics))
+It implements [full adder](<https://en.wikipedia.org/wiki/Adder_(electronics)>)
 electronics circuit logic to sum two 32-bit integers in two's complement format.
 It's using the boolean logic to cover all possible cases of adding two input bits:
 with and without a "carry bit" from adding the previous less-significant stage.
 
 Legend:
+
 - `A`: Number `A`
 - `B`: Number `B`
 - `ai`: ith bit of number `A`

src/algorithms/math/complex-number/README.fr-FR.md

@@ -0,0 +1,237 @@
+# Nombre complexe
+
+_Read this in other languages:_
+[english](README.md).
+
+Un **nombre complexe** est un nombre qui peut s'écrire sous la forme
+`a + b * i`, tels que `a` et `b` sont des nombres réels,
+et `i` est la solution de l'équation `x^2 = −1`.
+Du fait qu'aucun _nombre réel_ ne statisfait l'équation,
+`i` est appellé _nombre imaginaire_. Étant donné le nombre complexe `a + b * i`,
+`a` est appellé _partie réelle_, et `b`, _partie imaginaire_.
+
+![Complex Number](https://www.mathsisfun.com/numbers/images/complex-example.svg)
+
+Un nombre complexe est donc la combinaison
+d'un nombre réel et d'un nombre imaginaire :
+
+![Complex Number](https://www.mathsisfun.com/numbers/images/complex-number.svg)
+
+En géométrie, les nombres complexes étendent le concept
+de ligne de nombres sur une dimension à un _plan complexe à deux dimensions_
+en utilisant l'axe horizontal pour lepartie réelle
+et l'axe vertical pour la partie imaginaire. Le nombre complexe `a + b * i`
+peut être identifié avec le point `(a, b)` dans le plan complexe.
+
+Un nombre complexe dont la partie réelle est zéro est dit _imaginaire pur_;
+les points pour ces nombres se trouvent sur l'axe vertical du plan complexe.
+Un nombre complexe dont la partie imaginaire est zéro
+peut être considéré comme un _nombre réel_; son point
+se trouve sur l'axe horizontal du plan complexe.
+
+| Nombre complexe | Partie réelle | partie imaginaire |                  |
+| :-------------- | :-----------: | :---------------: | ---------------- |
+| 3 + 2i          |       3       |         2         |                  |
+| 5               |       5       |       **0**       | Purely Real      |
+| −6i             |     **0**     |        -6         | Purely Imaginary |
+
+A complex number can be visually represented as a pair of numbers `(a, b)` forming
+a vector on a diagram called an _Argand diagram_, representing the _complex plane_.
+`Re` is the real axis, `Im` is the imaginary axis, and `i` satisfies `i^2 = −1`.
+
+Un nombre complexe peut être représenté visuellement comme une paire de nombres
+`(a, b)` formant un vecteur sur un diagramme appelé _diagramme d'Argand_,
+représentant le _plan complexe_.
+_Re_ est l'axe réel, _Im_ est l'axe imaginaire et `i` satisfait `i^2 = −1`.
+
+![Complex Number](https://upload.wikimedia.org/wikipedia/commons/a/af/Complex_number_illustration.svg)
+
+> Complexe ne veut pas dire compliqué. Cela signifie simplement que
+> les deux types de nombres, réels et imaginaires, forment ensemble un complexe
+> comme on le dirait d'un complexe de bâtiments (bâtiments réunis).
+
+## Forme polaire
+
+Une manière de définir un point `P` dans le plan complexe, autre que d'utiliser
+les coordonnées x et y, consiste à utiliser la distance entre le point `O`, le point
+dont les coordonnées sont `(0, 0)` (l'origine), et l'angle sous-tendu
+entre l'axe réel positif et le segment de droite `OP` dans le sens antihoraire.
+Cette idée conduit à la forme polaire des nombres complexes.
+
+![Polar Form](https://upload.wikimedia.org/wikipedia/commons/7/7a/Complex_number_illustration_modarg.svg)
+
+The _valeur absolue_ (ou module) d'un nombre complexe `z = x + yi` est:
+
+![Radius](https://wikimedia.org/api/rest_v1/media/math/render/svg/b59629c801aa0ddcdf17ee489e028fb9f8d4ea75)
+
+L'argument de `z` (parfois appelé « phase » ou « amplitude ») est l'angle
+du rayon `OP` avec l'axe des réels positifs, et s'écrit `arg(z)`. Comme
+avec le module, l'argument peut être trouvé à partir de la forme rectangulaire `x + yi`:
+
+![Phase](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cbbdd9bb1dd5df86dd2b820b20f82995023e566)
+
+Ensemble, `r` et`φ` donnent une autre façon de représenter les nombres complexes, la
+forme polaire, car la combinaison du module et de l'argument suffit à indiquer la
+position d'un point sur le plan. Obtenir les coordonnées du rectangle d'origine
+à partir de la forme polaire se fait par la formule appelée forme trigonométrique :
+
+![Polar Form](https://wikimedia.org/api/rest_v1/media/math/render/svg/b03de1e1b7b049880b5e4870b68a57bc180ff6ce)
+
+En utilisant la formule d'Euler, cela peut être écrit comme suit:
+
+![Euler's Form](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a087c772212e7375cb321d83fc1fcc715cd0ed2)
+
+## Opérations de base
+
+### Addition
+
+Pour ajouter deux nombres complexes, nous ajoutons chaque partie séparément :
+
+```text
+(a + b * i) + (c + d * i) = (a + c) + (b + d) * i
+```
+
+**Exemple**
+
+```text
+(3 + 5i) + (4 − 3i) = (3 + 4) + (5 − 3)i = 7 + 2i
+```
+
+Dans un plan complexe, l'addition ressemblera à ceci:
+
+![Complex Addition](https://www.mathsisfun.com/algebra/images/complex-plane-vector-add.svg)
+
+### Soustraction
+
+Pour soustraire deux nombres complexes, on soustrait chaque partie séparément :
+
+```text
+(a + b * i) - (c + d * i) = (a - c) + (b - d) * i
+```
+
+**Exemple**
+
+```text
+(3 + 5i) - (4 − 3i) = (3 - 4) + (5 + 3)i = -1 + 8i
+```
+
+### Multiplication
+
+Pour multiplier les nombres complexes, chaque partie du premier nombre complexe est multipliée
+par chaque partie du deuxième nombre complexe:
+
+On peut utiliser le "FOIL" (parfois traduit PEID en français), acronyme de
+**F**irsts (Premiers), **O**uters (Extérieurs), **I**nners (Intérieurs), **L**asts (Derniers)" (
+voir [Binomial Multiplication](ttps://www.mathsisfun.com/algebra/polynomials-multiplying.html) pour plus de détails):
+
+![Complex Multiplication](https://www.mathsisfun.com/algebra/images/foil-complex.svg)
+
+- Firsts: `a × c`
+- Outers: `a × di`
+- Inners: `bi × c`
+- Lasts: `bi × di`
+
+En général, cela ressemble à:
+
+```text
+(a + bi)(c + di) = ac + adi + bci + bdi^2
+```
+
+Mais il existe aussi un moyen plus rapide !
+
+Utiliser cette loi:
+
+```text
+(a + bi)(c + di) = (ac − bd) + (ad + bc)i
+```
+
+**Exemple**
+
+```text
+(3 + 2i)(1 + 7i)
+= 3×1 + 3×7i + 2i×1+ 2i×7i
+= 3 + 21i + 2i + 14i^2
+= 3 + 21i + 2i − 14   (because i^2 = −1)
+= −11 + 23i
+```
+
+```text
+(3 + 2i)(1 + 7i) = (3×1 − 2×7) + (3×7 + 2×1)i = −11 + 23i
+```
+
+### Conjugués
+
+En mathématiques, le conjugué d'un nombre complexe z
+est le nombre complexe formé de la même partie réelle que z
+mais de partie imaginaire opposée.
+
+Un conjugué vois son signe changer au milieu comme suit:
+
+![Complex Conjugate](https://www.mathsisfun.com/numbers/images/complex-conjugate.svg)
+
+Un conjugué est souvent écrit avec un trait suscrit (barre au-dessus):
+
+```text
+______
+5 − 3i   =   5 + 3i
+```
+
+Dans un plan complexe, le nombre conjugué sera mirroir par rapport aux axes réels.
+
+![Complex Conjugate](https://upload.wikimedia.org/wikipedia/commons/6/69/Complex_conjugate_picture.svg)
+
+### Division
+
+Le conjugué est utiliser pour aider à la division de nombres complexes
+
+L'astuce est de _multiplier le haut et le bas par le conjugué du bas_.
+
+**Exemple**
+
+```text
+2 + 3i
+------
+4 − 5i
+```
+
+Multiplier le haut et le bas par le conjugué de `4 − 5i`:
+
+```text
+  (2 + 3i) * (4 + 5i)   8 + 10i + 12i + 15i^2
+= ------------------- = ----------------------
+  (4 − 5i) * (4 + 5i)   16 + 20i − 20i − 25i^2
+```
+
+Et puisque `i^2 = −1`, il s'ensuit que:
+
+```text
+  8 + 10i + 12i − 15    −7 + 22i   −7   22
+= ------------------- = -------- = -- + -- * i
+  16 + 20i − 20i + 25      41      41   41
+
+```
+
+Il existe cependant un moyen plus direct.
+
+Dans l'exemple précédent, ce qui s'est passé en bas était intéressant:
+
+```text
+(4 − 5i)(4 + 5i) = 16 + 20i − 20i − 25i
+```
+
+Les termes du milieu `(20i − 20i)` s'annule! Et pusique `i^2 = −1` on retrouve:
+
+```text
+(4 − 5i)(4 + 5i) = 4^2 + 5^2
+```
+
+Ce qui est vraiment un résultat assez simple. La règle générale est:
+
+```text
+(a + bi)(a − bi) = a^2 + b^2
+```
+
+## Références
+
+- [Wikipedia](https://fr.wikipedia.org/wiki/Nombre_complexe)
+- [Math is Fun](https://www.mathsisfun.com/numbers/complex-numbers.html)

src/algorithms/math/complex-number/README.md

@@ -1,11 +1,14 @@
 # Complex Number
 
-A **complex number** is a number that can be expressed in the 
+_Read this in other languages:_
+[français](README.fr-FR.md).
+
+A **complex number** is a number that can be expressed in the
 form `a + b * i`, where `a` and `b` are real numbers, and `i` is a solution of
-the equation `x^2 = −1`. Because no *real number* satisfies this 
-equation, `i` is called an *imaginary number*. For the complex 
-number `a + b * i`, `a` is called the *real part*, and `b` is called 
-the *imaginary part*.
+the equation `x^2 = −1`. Because no _real number_ satisfies this
+equation, `i` is called an _imaginary number_. For the complex
+number `a + b * i`, `a` is called the _real part_, and `b` is called
+the _imaginary part_.
 
 ![Complex Number](https://www.mathsisfun.com/numbers/images/complex-example.svg)
 
@@ -13,56 +16,56 @@ A Complex Number is a combination of a Real Number and an Imaginary Number:
 
 ![Complex Number](https://www.mathsisfun.com/numbers/images/complex-number.svg)
 
-Geometrically, complex numbers extend the concept of the one-dimensional number 
-line to the *two-dimensional complex plane* by using the horizontal axis for the
-real part and the vertical axis for the imaginary part. The complex 
-number `a + b * i` can be identified with the point `(a, b)` in the complex plane.
+Geometrically, complex numbers extend the concept of the one-dimensional number
+line to the _two-dimensional complex plane_ by using the horizontal axis for the
+real part and the vertical axis for the imaginary part. The complex
+number `a + b * i` can be identified with the point `(a, b)` in the complex plane.
 
-A complex number whose real part is zero is said to be *purely imaginary*; the
+A complex number whose real part is zero is said to be _purely imaginary_; the
 points for these numbers lie on the vertical axis of the complex plane. A complex
-number whose imaginary part is zero can be viewed as a *real number*; its point 
+number whose imaginary part is zero can be viewed as a _real number_; its point
 lies on the horizontal axis of the complex plane.
 
-| Complex Number | Real Part | Imaginary Part |     |
-| :------------- | :-------: | :------------: | --- |
-| 3 + 2i         | 3         | 2              |     |
-| 5              | 5         | **0**          | Purely Real |
-| −6i            | **0**     | -6             | Purely Imaginary |
+| Complex Number | Real Part | Imaginary Part |                  |
+| :------------- | :-------: | :------------: | ---------------- |
+| 3 + 2i         |     3     |       2        |                  |
+| 5              |     5     |     **0**      | Purely Real      |
+| −6i            |   **0**   |       -6       | Purely Imaginary |
 
-A complex number can be visually represented as a pair of numbers `(a, b)` forming 
-a vector on a diagram called an *Argand diagram*, representing the *complex plane*.
+A complex number can be visually represented as a pair of numbers `(a, b)` forming
+a vector on a diagram called an _Argand diagram_, representing the _complex plane_.
 `Re` is the real axis, `Im` is the imaginary axis, and `i` satisfies `i^2 = −1`.
 
 ![Complex Number](https://upload.wikimedia.org/wikipedia/commons/a/af/Complex_number_illustration.svg)
 
-> Complex does not mean complicated. It means the two types of numbers, real and 
-imaginary, together form a complex, just like a building complex (buildings 
-joined together).
+> Complex does not mean complicated. It means the two types of numbers, real and
+> imaginary, together form a complex, just like a building complex (buildings
+> joined together).
 
 ## Polar Form
 
-An alternative way of defining a point `P` in the complex plane, other than using 
+An alternative way of defining a point `P` in the complex plane, other than using
 the x- and y-coordinates, is to use the distance of the point from `O`, the point
-whose coordinates are `(0, 0)` (the origin), together with the angle subtended 
-between the positive real axis and the line segment `OP` in a counterclockwise 
+whose coordinates are `(0, 0)` (the origin), together with the angle subtended
+between the positive real axis and the line segment `OP` in a counterclockwise
 direction. This idea leads to the polar form of complex numbers.
 
 ![Polar Form](https://upload.wikimedia.org/wikipedia/commons/7/7a/Complex_number_illustration_modarg.svg)
 
-The *absolute value* (or modulus or magnitude) of a complex number `z = x + yi` is:
+The _absolute value_ (or modulus or magnitude) of a complex number `z = x + yi` is:
 
 ![Radius](https://wikimedia.org/api/rest_v1/media/math/render/svg/b59629c801aa0ddcdf17ee489e028fb9f8d4ea75)
 
 The argument of `z` (in many applications referred to as the "phase") is the angle
-of the radius `OP` with the positive real axis, and is written as `arg(z)`. As 
+of the radius `OP` with the positive real axis, and is written as `arg(z)`. As
 with the modulus, the argument can be found from the rectangular form `x+yi`:
 
 ![Phase](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cbbdd9bb1dd5df86dd2b820b20f82995023e566)
 
-Together, `r` and `φ` give another way of representing complex numbers, the 
-polar form, as the combination of modulus and argument fully specify the 
-position of a point on the plane. Recovering the original rectangular 
-co-ordinates from the polar form is done by the formula called trigonometric 
+Together, `r` and `φ` give another way of representing complex numbers, the
+polar form, as the combination of modulus and argument fully specify the
+position of a point on the plane. Recovering the original rectangular
+co-ordinates from the polar form is done by the formula called trigonometric
 form:
 
 ![Polar Form](https://wikimedia.org/api/rest_v1/media/math/render/svg/b03de1e1b7b049880b5e4870b68a57bc180ff6ce)
@@ -107,7 +110,7 @@ To subtract two complex numbers we subtract each part separately:
 
 ### Multiplying
 
-To multiply complex numbers each part of the first complex number gets multiplied 
+To multiply complex numbers each part of the first complex number gets multiplied
 by each part of the second complex number:
 
 Just use "FOIL", which stands for "**F**irsts, **O**uters, **I**nners, **L**asts" (
@@ -138,7 +141,7 @@ Use this rule:
 **Example**
 
 ```text
-(3 + 2i)(1 + 7i) 
+(3 + 2i)(1 + 7i)
 = 3×1 + 3×7i + 2i×1+ 2i×7i
 = 3 + 21i + 2i + 14i^2
 = 3 + 21i + 2i − 14   (because i^2 = −1)
@@ -164,7 +167,7 @@ ______
 5 − 3i   =   5 + 3i
 ```
 
-On the complex plane the conjugate number will be mirrored against real axes. 
+On the complex plane the conjugate number will be mirrored against real axes.
 
 ![Complex Conjugate](https://upload.wikimedia.org/wikipedia/commons/6/69/Complex_conjugate_picture.svg)
 
@@ -172,7 +175,7 @@ On the complex plane the conjugate number will be mirrored against real axes.
 
 The conjugate is used to help complex division.
 
-The trick is to *multiply both top and bottom by the conjugate of the bottom*.
+The trick is to _multiply both top and bottom by the conjugate of the bottom_.
 
 **Example**
 
@@ -207,7 +210,7 @@ In the previous example, what happened on the bottom was interesting:
 (4 − 5i)(4 + 5i) = 16 + 20i − 20i − 25i
 ```
 
-The middle terms `(20i − 20i)` cancel out!	Also `i^2 = −1` so we end up with this:
+The middle terms `(20i − 20i)` cancel out! Also `i^2 = −1` so we end up with this:
 
 ```text
 (4 − 5i)(4 + 5i) = 4^2 + 5^2

src/algorithms/math/euclidean-algorithm/README.fr-FR.md

@@ -0,0 +1,49 @@
+# Algorithme d'Euclide
+
+_Read this in other languages:_
+[english](README.md).
+
+En mathématiques, l'algorithme d'Euclide est un algorithme qui calcule le plus grand commun diviseur (PGCD) de deux entiers, c'est-à-dire le plus grand entier qui divise les deux entiers, en laissant un reste nul. L'algorithme ne connaît pas la factorisation de ces deux nombres.
+
+Le PGCD de deux entiers relatifs est égal au PGCD de leurs valeurs absolues : de ce fait, on se restreint dans cette section aux entiers positifs. L'algorithme part du constat suivant : le PGCD de deux nombres n'est pas changé si on remplace le plus grand d'entre eux par leur différence. Autrement dit, `pgcd(a, b) = pgcd(b, a - b)`. Par exemple, le PGCD de `252` et `105` vaut `21` (en effet, `252 = 21 × 12` and `105 = 21 × 5`), mais c'est aussi le PGCD de `252 - 105 = 147` et `105`. Ainsi, comme le remplacement de ces nombres diminue strictement le plus grand d'entre eux, on peut continuer le processus, jusqu'à obtenir deux nombres égaux.
+
+En inversant les étapes, le PGCD peut être exprimé comme une somme de
+les deux nombres originaux, chacun étant multiplié
+par un entier positif ou négatif, par exemple `21 = 5 × 105 + (-2) × 252`.
+Le fait que le PGCD puisse toujours être exprimé de cette manière est
+connue sous le nom de Théorème de Bachet-Bézout.
+
+![GCD](https://upload.wikimedia.org/wikipedia/commons/3/37/Euclid%27s_algorithm_Book_VII_Proposition_2_3.png)
+
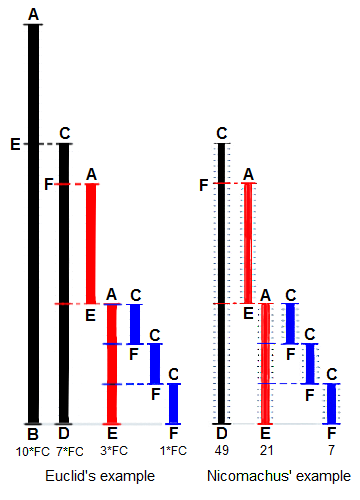
+La Méthode d'Euclide pour trouver le plus grand diviseur commun (PGCD)
+de deux longueurs de départ`BA` et `DC`, toutes deux définies comme étant
+multiples d'une longueur commune. La longueur `DC` étant
+plus courte, elle est utilisée pour « mesurer » `BA`, mais une seule fois car
+le reste `EA` est inférieur à `DC`. `EA` mesure maintenant (deux fois)
+la longueur la plus courte `DC`, le reste `FC` étant plus court que `EA`.
+Alors `FC` mesure (trois fois) la longueur `EA`. Parce qu'il y a
+pas de reste, le processus se termine par `FC` étant le « PGCD ».
+À droite, l'exemple de Nicomaque de Gérase avec les nombres `49` et `21`
+ayan un PGCD de `7` (dérivé de Heath 1908: 300).
+
+![GCD](https://upload.wikimedia.org/wikipedia/commons/7/74/24x60.svg)
+
+Un de rectangle de dimensions `24 par 60` peux se carreler en carrés de `12 par 12`,
+puisque `12` est le PGCD ed `24` et `60`. De façon générale,
+un rectangle de dimension `a par b` peut se carreler en carrés
+de côté `c`, seulement si `c` est un diviseur commun de `a` et `b`.
+
+![GCD](https://upload.wikimedia.org/wikipedia/commons/1/1c/Euclidean_algorithm_1071_462.gif)
+
+Animation basée sur la soustraction via l'algorithme euclidien.
+Le rectangle initial a les dimensions `a = 1071` et `b = 462`.
+Des carrés de taille `462 × 462` y sont placés en laissant un
+rectangle de `462 × 147`. Ce rectangle est carrelé avec des
+carrés de `147 × 147` jusqu'à ce qu'un rectangle de `21 × 147` soit laissé,
+qui à son tour estcarrelé avec des carrés `21 × 21`,
+ne laissant aucune zone non couverte.
+La plus petite taille carrée, `21`, est le PGCD de `1071` et `462`.
+
+## References
+
+[Wikipedia](https://fr.wikipedia.org/wiki/Algorithme_d%27Euclide)

src/algorithms/math/euclidean-algorithm/README.md

@@ -1,55 +1,58 @@
 # Euclidean algorithm
 
-In mathematics, the Euclidean algorithm, or Euclid's algorithm, 
-is an efficient method for computing the greatest common divisor 
-(GCD) of two numbers, the largest number that divides both of 
+_Read this in other languages:_
+[français](README.fr-FR.md).
+
+In mathematics, the Euclidean algorithm, or Euclid's algorithm,
+is an efficient method for computing the greatest common divisor
+(GCD) of two numbers, the largest number that divides both of
 them without leaving a remainder.
 
-The Euclidean algorithm is based on the principle that the 
-greatest common divisor of two numbers does not change if 
-the larger number is replaced by its difference with the 
-smaller number. For example, `21` is the GCD of `252` and 
-`105` (as `252 = 21 × 12` and `105 = 21 × 5`), and the same 
-number `21` is also the GCD of `105` and `252 − 105 = 147`. 
-Since this replacement reduces the larger of the two numbers, 
-repeating this process gives successively smaller pairs of 
-numbers until the two numbers become equal. 
-When that occurs, they are the GCD of the original two numbers. 
+The Euclidean algorithm is based on the principle that the
+greatest common divisor of two numbers does not change if
+the larger number is replaced by its difference with the
+smaller number. For example, `21` is the GCD of `252` and
+`105` (as `252 = 21 × 12` and `105 = 21 × 5`), and the same
+number `21` is also the GCD of `105` and `252 − 105 = 147`.
+Since this replacement reduces the larger of the two numbers,
+repeating this process gives successively smaller pairs of
+numbers until the two numbers become equal.
+When that occurs, they are the GCD of the original two numbers.
 
-By reversing the steps, the GCD can be expressed as a sum of 
-the two original numbers each multiplied by a positive or 
-negative integer, e.g., `21 = 5 × 105 + (−2) × 252`. 
-The fact that the GCD can always be expressed in this way is 
+By reversing the steps, the GCD can be expressed as a sum of
+the two original numbers each multiplied by a positive or
+negative integer, e.g., `21 = 5 × 105 + (−2) × 252`.
+The fact that the GCD can always be expressed in this way is
 known as Bézout's identity.
 
 ![GCD](https://upload.wikimedia.org/wikipedia/commons/3/37/Euclid%27s_algorithm_Book_VII_Proposition_2_3.png)
 
-Euclid's method for finding the greatest common divisor (GCD) 
-of two starting lengths `BA` and `DC`, both defined to be 
-multiples of a common "unit" length. The length `DC` being 
-shorter, it is used to "measure" `BA`, but only once because 
-remainder `EA` is less than `DC`. EA now measures (twice) 
-the shorter length `DC`, with remainder `FC` shorter than `EA`. 
-Then `FC` measures (three times) length `EA`. Because there is 
-no remainder, the process ends with `FC` being the `GCD`. 
-On the right Nicomachus' example with numbers `49` and `21` 
+Euclid's method for finding the greatest common divisor (GCD)
+of two starting lengths `BA` and `DC`, both defined to be
+multiples of a common "unit" length. The length `DC` being
+shorter, it is used to "measure" `BA`, but only once because
+remainder `EA` is less than `DC`. EA now measures (twice)
+the shorter length `DC`, with remainder `FC` shorter than `EA`.
+Then `FC` measures (three times) length `EA`. Because there is
+no remainder, the process ends with `FC` being the `GCD`.
+On the right Nicomachus' example with numbers `49` and `21`
 resulting in their GCD of `7` (derived from Heath 1908:300).
 
 ![GCD](https://upload.wikimedia.org/wikipedia/commons/7/74/24x60.svg)
 
-A `24-by-60` rectangle is covered with ten `12-by-12` square 
-tiles, where `12` is the GCD of `24` and `60`. More generally, 
-an `a-by-b` rectangle can be covered with square tiles of 
+A `24-by-60` rectangle is covered with ten `12-by-12` square
+tiles, where `12` is the GCD of `24` and `60`. More generally,
+an `a-by-b` rectangle can be covered with square tiles of
 side-length `c` only if `c` is a common divisor of `a` and `b`.
 
 ![GCD](https://upload.wikimedia.org/wikipedia/commons/1/1c/Euclidean_algorithm_1071_462.gif)
 
-Subtraction-based animation of the Euclidean algorithm. 
-The initial rectangle has dimensions `a = 1071` and `b = 462`. 
-Squares of size `462×462` are placed within it leaving a 
-`462×147` rectangle. This rectangle is tiled with `147×147` 
-squares until a `21×147` rectangle is left, which in turn is 
-tiled with `21×21` squares, leaving no uncovered area. 
+Subtraction-based animation of the Euclidean algorithm.
+The initial rectangle has dimensions `a = 1071` and `b = 462`.
+Squares of size `462×462` are placed within it leaving a
+`462×147` rectangle. This rectangle is tiled with `147×147`
+squares until a `21×147` rectangle is left, which in turn is
+tiled with `21×21` squares, leaving no uncovered area.
 The smallest square size, `21`, is the GCD of `1071` and `462`.
 
 ## References

src/algorithms/math/factorial/README.fr-FR.md

@@ -0,0 +1,35 @@
+# Factorielle
+
+_Lisez ceci dans d'autres langues:_
+[english](README.md), [_简体中文_](README.zh-CN.md).
+
+En mathématiques, la factorielle d'un entier naturel `n`,
+notée avec un point d'exclamation `n!`, est le produit des nombres entiers
+strictement positifs inférieurs ou égaux à n. Par exemple:
+
+```
+5! = 5 * 4 * 3 * 2 * 1 = 120
+```
+
+| n   |                n! |
+| --- | ----------------: |
+| 0   |                 1 |
+| 1   |                 1 |
+| 2   |                 2 |
+| 3   |                 6 |
+| 4   |                24 |
+| 5   |               120 |
+| 6   |               720 |
+| 7   |             5 040 |
+| 8   |            40 320 |
+| 9   |           362 880 |
+| 10  |         3 628 800 |
+| 11  |        39 916 800 |
+| 12  |       479 001 600 |
+| 13  |     6 227 020 800 |
+| 14  |    87 178 291 200 |
+| 15  | 1 307 674 368 000 |
+
+## References
+
+[Wikipedia](https://fr.wikipedia.org/wiki/Factorielle)

src/algorithms/math/factorial/README.md

@@ -1,34 +1,34 @@
 # Factorial
 
 _Read this in other languages:_
-[_简体中文_](README.zh-CN.md),
+[_简体中文_](README.zh-CN.md), [français](README.fr-FR.md).
 
-In mathematics, the factorial of a non-negative integer `n`, 
-denoted by `n!`, is the product of all positive integers less 
+In mathematics, the factorial of a non-negative integer `n`,
+denoted by `n!`, is the product of all positive integers less
 than or equal to `n`. For example:
 
 ```
 5! = 5 * 4 * 3 * 2 * 1 = 120
 ```
 
-| n     | n!                          | 
-| ----- | --------------------------: |
-| 0     | 1                           |
-| 1     | 1                           |
-| 2     | 2                           |
-| 3     | 6                           |
-| 4     | 24                          |
-| 5     | 120                         |
-| 6     | 720                         |
-| 7     | 5 040                       |
-| 8     | 40 320                      |
-| 9     | 362 880                     |
-| 10    | 3 628 800                   |
-| 11    | 39 916 800                  |
-| 12    | 479 001 600                 |
-| 13    | 6 227 020 800               |
-| 14    | 87 178 291 200              |
-| 15    | 1 307 674 368 000           |
+| n   |                n! |
+| --- | ----------------: |
+| 0   |                 1 |
+| 1   |                 1 |
+| 2   |                 2 |
+| 3   |                 6 |
+| 4   |                24 |
+| 5   |               120 |
+| 6   |               720 |
+| 7   |             5 040 |
+| 8   |            40 320 |
+| 9   |           362 880 |
+| 10  |         3 628 800 |
+| 11  |        39 916 800 |
+| 12  |       479 001 600 |
+| 13  |     6 227 020 800 |
+| 14  |    87 178 291 200 |
+| 15  | 1 307 674 368 000 |
 
 ## References
 

src/algorithms/math/fast-powering/README.fr-FR.md

@@ -0,0 +1,73 @@
+# Algorithme d'exponentiation rapide
+
+_Read this in other languages:_
+[english](README.md).
+
+En algèbre, une **puissance** d'un nombre est le résultat de la multiplication répétée de ce nombre avec lui-même.
+
+Elle est souvent notée en assortissant le nombre d'un entier, typographié en exposant, qui indique le nombre de fois qu'apparaît le nombre comme facteur dans cette multiplication.
+
+![Power](https://www.mathsisfun.com/algebra/images/exponent-8-2.svg)
+
+## Implémentation « naïve »
+
+Comment trouver `a` élevé à la puissance `b` ?
+
+On multiplie `a` avec lui-même, `b` nombre de fois.
+Ainsi, `a^b = a * a * a * ... * a` (`b` occurrences de `a`).
+
+Cette opération aura un complexité linéaire, notée `O(n)`,
+car la multiplication aura lieu exactement `n` fois.
+
+## Algorithme d'exponentiation rapide
+
+Peut-on faire mieux que cette implémentation naïve?
+Oui, on peut réduire le nombre de puissance à un complexité de `O(log(n))`.
+
+Cet algorithme utilise l'approche « diviser pour mieux régner »
+pour calculer cette puissance.
+En l'état, cet algorithme fonctionne pour deux entiers positifs `X` et `Y`.
+
+L'idée derrière cet algorithme est basée sur l'observation suivante.
+
+Lorsque `Y` est **pair**:
+
+```text
+X^Y = X^(Y/2) * X^(Y/2)
+```
+
+Lorsque `Y` est **impair**:
+
+```text
+X^Y = X^(Y//2) * X^(Y//2) * X
+où Y//2 est le résultat de la division entière de Y par 2.
+```
+
+**Par exemple**
+
+```text
+2^4 = (2 * 2) * (2 * 2) = (2^2) * (2^2)
+```
+
+```text
+2^5 = (2 * 2) * (2 * 2) * 2 = (2^2) * (2^2) * (2)
+```
+
+Ainsi, puisqu'à chaque étape on doits calculer
+deux fois la même puissance `X ^ (Y / 2)`,
+on peut optimiser en l'enregistrant dans une variable intermédiaire
+pour éviter son calcul en double.
+
+**Complexité en temps**
+
+Comme à chaque itération nous réduisons la puissance de moitié,
+nous appelons récursivement la fonction `log(n)` fois. Le complexité de temps de cet algorithme est donc réduite à:
+
+```text
+O(log(n))
+```
+
+## Références
+
+- [YouTube](https://www.youtube.com/watch?v=LUWavfN9zEo&index=80&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&t=0s)
+- [Wikipedia](https://fr.wikipedia.org/wiki/Exponentiation_rapide)

src/algorithms/math/fast-powering/README.md

@@ -1,6 +1,9 @@
 # Fast Powering Algorithm
 
-**The power of a number** says how many times to use the number in a 
+_Read this in other languages:_
+[français](README.fr-FR.md).
+
+**The power of a number** says how many times to use the number in a
 multiplication.
 
 It is written as a small number to the right and above the base number.
@@ -11,7 +14,7 @@ It is written as a small number to the right and above the base number.
 
 How to find `a` raised to the power `b`?
 
-We multiply `a` to itself, `b` times. That 
+We multiply `a` to itself, `b` times. That
 is, `a^b = a * a * a * ... * a` (`b` occurrences of `a`).
 
 This operation will take `O(n)` time since we need to do multiplication operation
@@ -20,9 +23,9 @@ exactly `n` times.
 ## Fast Power Algorithm
 
 Can we do better than naive algorithm does? Yes we may solve the task of
- powering in `O(log(n))` time.
+powering in `O(log(n))` time.
 
-The algorithm uses divide and conquer approach to compute power. Currently the 
+The algorithm uses divide and conquer approach to compute power. Currently the
 algorithm work for two positive integers `X` and `Y`.
 
 The idea behind the algorithm is based on the fact that:
@@ -30,7 +33,7 @@ The idea behind the algorithm is based on the fact that:
 For **even** `Y`:
 
 ```text
-X^Y = X^(Y/2) * X^(Y/2) 
+X^Y = X^(Y/2) * X^(Y/2)
 ```
 
 For **odd** `Y`:
@@ -50,17 +53,17 @@ where Y//2 is result of division of Y by 2 without reminder.
 2^5 = (2 * 2) * (2 * 2) * 2 = (2^2) * (2^2) * (2)
 ```
 
-Now, since on each step we need to compute the same `X^(Y/2)` power twice we may optimise 
-it by saving it to some intermediate variable to avoid its duplicate calculation. 
+Now, since on each step we need to compute the same `X^(Y/2)` power twice we may optimise
+it by saving it to some intermediate variable to avoid its duplicate calculation.
 
 **Time Complexity**
 
-Since each iteration we split the power by half then we will call function 
+Since each iteration we split the power by half then we will call function
 recursively `log(n)` times. This the time complexity of the algorithm is reduced to:
 
 ```text
 O(log(n))
-``` 
+```
 
 ## References
 

src/algorithms/math/fibonacci/README.fr-FR.md

@@ -0,0 +1,23 @@
+# Nombre de Fibonacci
+
+_Read this in other languages:_
+[english](README.md).
+
+En mathématiques, la suite de Fibonacci est une suite d'entiers
+dans laquelle chaque terme (après les deux premiers)
+est la somme des deux termes qui le précèdent.
+Les termes de cette suite sont appelés nombres de Fibonacci:
+
+`0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...`
+
+Les carrés de Fibonacci en spirale s'ajustent ensemble pour former une spirale d'or.
+
+![Fibonacci](https://upload.wikimedia.org/wikipedia/commons/d/db/34%2A21-FibonacciBlocks.png)
+
+La spirale de Fibonacci: approximation d'une spirale d'or créée en dessinant des arcs de cercle reliant les coins opposés de carrés dans un pavage Fibonacci[4] . Celui-ci utilise des carrés de tailles 1, 1, 2, 3, 5, 8, 13, 21, et 34.
+
+![Fibonacci Spiral](https://upload.wikimedia.org/wikipedia/commons/2/2e/FibonacciSpiral.svg)
+
+## References
+
+- [Wikipedia](https://fr.wikipedia.org/wiki/Suite_de_Fibonacci)

src/algorithms/math/fibonacci/README.md

@@ -1,8 +1,11 @@
 # Fibonacci Number
 
-In mathematics, the Fibonacci numbers are the numbers in the following 
-integer sequence, called the Fibonacci sequence, and characterized by 
-the fact that every number after the first two is the sum of the two 
+_Read this in other languages:_
+[français](README.fr-FR.md).
+
+In mathematics, the Fibonacci numbers are the numbers in the following
+integer sequence, called the Fibonacci sequence, and characterized by
+the fact that every number after the first two is the sum of the two
 preceding ones:
 
 `0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...`

src/algorithms/math/fourier-transform/README.fr-FR.md

@@ -0,0 +1,135 @@
+# Transformation de Fourier
+
+_Read this in other languages:_
+[english](README.md).
+
+## Définitions
+
+La transformation de Fourier (**ℱ**) est une opération qui transforme
+une fonction intégrable sur ℝ en une autre fonction,
+décrivant le spectre fréquentiel de cette dernière
+
+La **Transformée de Fourier Discrète** (**TFD**) convertit une séquence finie d'échantillons également espacés d'une fonction, dans une séquence de même longueur d'échantillons, également espacés de la Transformée de Fourier à temps discret (TFtd), qui est une fonction complexe de la fréquence.
+L'intervalle auquel le TFtd est échantillonné est l'inverse de la durée de la séquence d'entrée.
+Une TFD inverse est une série de Fourier, utilisant les échantillons TFtd comme coefficients de sinusoïdes complexes aux fréquences TFtd correspondantes. Elle a les mêmes valeurs d'échantillonnage que la
+séquence d'entrée originale. On dit donc que la TFD est une représentation du domaine fréquentiel
+de la séquence d'entrée d'origine. Si la séquence d'origine couvre toutes les
+valeurs non nulles d'une fonction, sa TFtd est continue (et périodique), et la TFD fournit
+les échantillons discrets d'une fenêtre. Si la séquence d'origine est un cycle d'une fonction périodique, la TFD fournit toutes les valeurs non nulles d'une fenêtre TFtd.
+
+Transformée de Fourier Discrète converti une séquence de `N` nombres complexes:
+
+{x<sub>n</sub>} = x<sub>0</sub>, x<sub>1</sub>, x<sub>2</sub> ..., x<sub>N-1</sub>
+
+en une atre séquence de nombres complexes::
+
+{X<sub>k</sub>} = X<sub>0</sub>, X<sub>1</sub>, X<sub>2</sub> ..., X<sub>N-1</sub>
+
+décrite par:
+
+![DFT](https://wikimedia.org/api/rest_v1/media/math/render/svg/1af0a78dc50bbf118ab6bd4c4dcc3c4ff8502223)
+
+The **Transformée de Fourier à temps discret** (**TFtd**) est une forme d'analyse de Fourier
+qui s'applique aux échantillons uniformément espacés d'une fonction continue. Le terme "temps discret" fait référence au fait que la transformée fonctionne sur des données discrètes
+(échantillons) dont l'intervalle a souvent des unités de temps.
+À partir des seuls échantillons, elle produit une fonction de fréquence qui est une somme périodique de la
+Transformée de Fourier continue de la fonction continue d'origine.
+
+A **Transformation de Fourier rapide** (**FFT** pour Fast Fourier Transform) est un algorithme de calcul de la transformation de Fourier discrète (TFD). Il est couramment utilisé en traitement numérique du signal pour transformer des données discrètes du domaine temporel dans le domaine fréquentiel, en particulier dans les oscilloscopes numériques (les analyseurs de spectre utilisant plutôt des filtres analogiques, plus précis). Son efficacité permet de réaliser des filtrages en modifiant le spectre et en utilisant la transformation inverse (filtre à réponse impulsionnelle finie).
+
+Cette transformation peut être illustée par la formule suivante. Sur la période de temps mesurée
+dans le diagramme, le signal contient 3 fréquences dominantes distinctes.
+
+Vue d'un signal dans le domaine temporel et fréquentiel:
+
+![FFT](https://upload.wikimedia.org/wikipedia/commons/6/61/FFT-Time-Frequency-View.png)
+
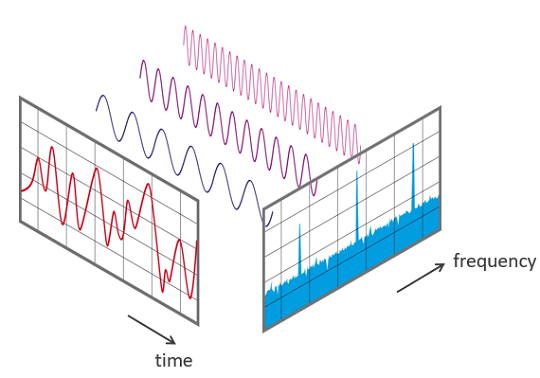
+An FFT algorithm computes the discrete Fourier transform (DFT) of a sequence, or
+its inverse (IFFT). Fourier analysis converts a signal from its original domain
+to a representation in the frequency domain and vice versa. An FFT rapidly
+computes such transformations by factorizing the DFT matrix into a product of
+sparse (mostly zero) factors. As a result, it manages to reduce the complexity of
+computing the DFT from O(n<sup>2</sup>), which arises if one simply applies the
+definition of DFT, to O(n log n), where n is the data size.
+
+Un algorithme FFT calcule la Transformée de Fourier discrète (TFD) d'une séquence, ou
+son inverse (IFFT). L'analyse de Fourier convertit un signal de son domaine d'origine
+en une représentation dans le domaine fréquentiel et vice versa. Une FFT
+calcule rapidement ces transformations en factorisant la matrice TFD en un produit de
+facteurs dispersés (généralement nuls). En conséquence, il parvient à réduire la complexité de
+calcul de la TFD de O (n <sup> 2 </sup>), qui survient si l'on applique simplement la
+définition de TFD, à O (n log n), où n est la taille des données.
+
+Voici une analyse de Fourier discrète d'une somme d'ondes cosinus à 10, 20, 30, 40,
+et 50 Hz:
+
+![FFT](https://upload.wikimedia.org/wikipedia/commons/6/64/FFT_of_Cosine_Summation_Function.png)
+
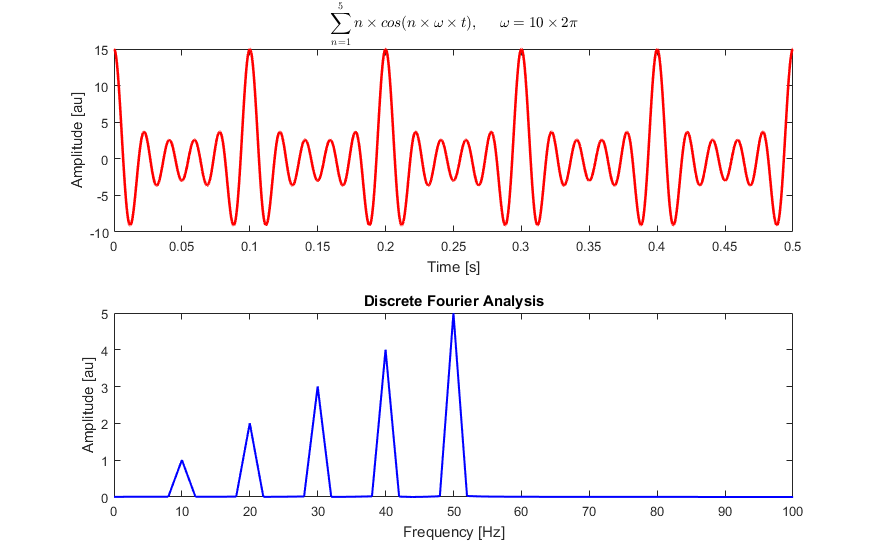
+## Explanation
+
+La Transformée de Fourier est l'une des connaissances les plus importante jamais découverte. Malheureusement, le
+son sens est enfoui dans des équations denses::
+
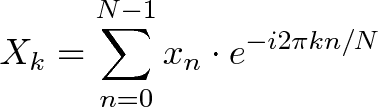
+![](https://betterexplained.com/wp-content/plugins/wp-latexrender/pictures/45c088dbb767150fc0bacfeb49dd49e5.png)
+
+et
+
+![](https://betterexplained.com/wp-content/plugins/wp-latexrender/pictures/faeb9c5bf2e60add63ae4a70b293c7b4.png)
+
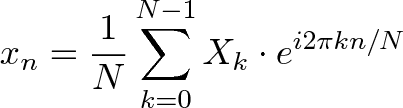
+Plutôt que se noyer dans les symboles, faisons en premier lieu l'expérience de l'idée principale. Voici une métaphore en français simple:
+
+- _Que fait la transformée de Fourier ?_ A partir d'un smoothie, elle trouve sa recette.
+- _Comment ?_ Elle passe le smoothie dans un filtre pour en extraire chaque ingrédient.
+- _Pourquoi ?_ Les recettes sont plus faciles à analyser, comparer et modifier que le smoothie lui-même.
+- _Comment récupérer le smoothie ?_ Re-mélanger les ingrédients.
+
+**Pensez en cercles, pas seulement en sinusoïdes**
+
+La transformée de Fourier concerne des trajectoires circulaires (pas les sinusoïdes 1-d)
+et la formuled'Euler est une manière intelligente d'en générer une:
+
+![](https://betterexplained.com/wp-content/uploads/euler/equal_paths.png)
+
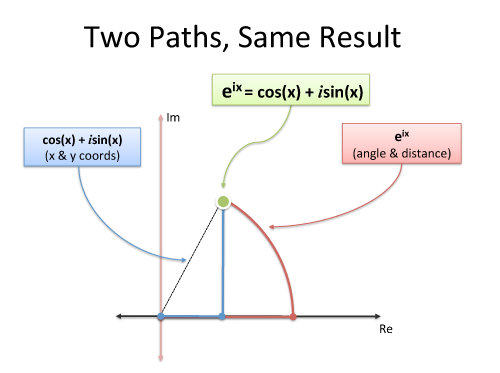
+Doit-on utiliser des exposants imaginaires pour se déplacer en cercle ? Non. Mais c'est pratique
+et compact. Et bien sûr, nous pouvons décrire notre chemin comme un mouvement coordonné en deux
+dimensions (réelle et imaginaire), mais n'oubliez pas la vue d'ensemble: nous sommes juste
+en déplacement dans un cercle.
+
+**À la découverte de la transformation complète**
+
+L'idée générale: notre signal n'est qu'un tas de pics de temps, d'instant T ! Si nous combinons les
+recettes pour chaque pic de temps, nous devrions obtenir la recette du signal complet.
+
+La transformée de Fourier construit cette recette fréquence par fréquence:
+
+![](https://betterexplained.com/wp-content/uploads/images/fourier-explained-20121219-224649.png)
+
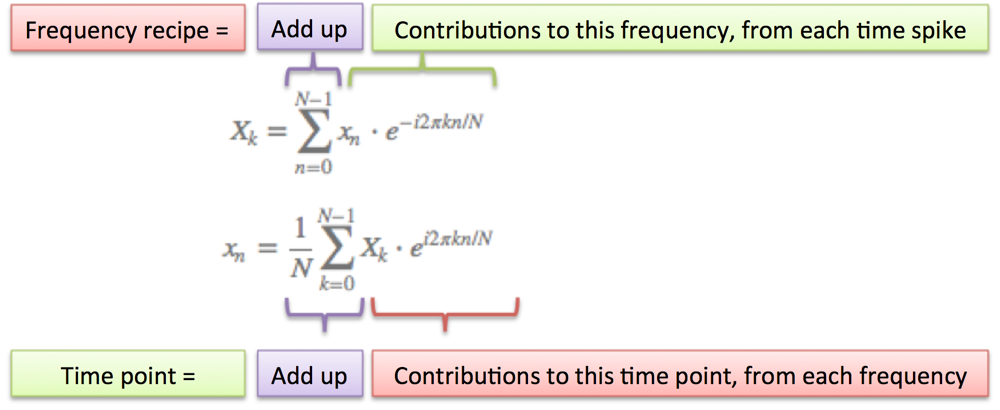
+Quelques notes
+
+- N = nombre d'échantillons de temps dont nous disposons
+- n = échantillon actuellement étudié (0 ... N-1)
+- x<sub>n</sub> = valeur du signal au temps n
+- k = fréquence actuellement étudiée (0 Hertz up to N-1 Hertz)
+- X<sub>k</sub> = quantité de fréquence k dans le signal (amplitude et phase, un nombre complexe)
+- Le facteur 1 / N est généralement déplacé vers la transformée inverse (passant des fréquences au temps). Ceci est autorisé, bien que je préfère 1 / N dans la transformation directe car cela donne les tailles réelles des pics de temps. Vous pouvez être plus ambitieux et utiliser 1 / racine carrée de (N) sur les deux transformations (aller en avant et en arrière crée le facteur 1 / N).
+- n/N est le pourcentage du temps que nous avons passé. 2 _ pi _ k est notre vitesse en radians/s. e ^ -ix est notre chemin circulaire vers l'arrière. La combinaison est la distance parcourue, pour cette vitesse et ce temps.
+- Les équations brutes de la transformée de Fourier consiste simplement à "ajouter les nombres complexes". De nombreux langages de programmation ne peuvent pas gérer directement les nombres complexes, on converti donc tout en coordonnées rectangulaires, pour les ajouter.
+
+Stuart Riffle a une excellente interprétation de la transformée de Fourier:
+
+![](https://betterexplained.com/wp-content/uploads/images/DerivedDFT.png)
+
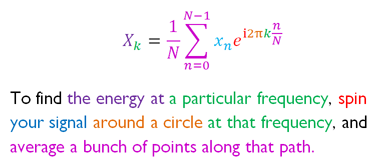
+## Références
+
+- Wikipedia
+
+  - [TF](https://fr.wikipedia.org/wiki/Transformation_de_Fourier)
+  - [TFD](https://fr.wikipedia.org/wiki/Transformation_de_Fourier_discr%C3%A8te)
+  - [FFT](https://fr.wikipedia.org/wiki/Transformation_de_Fourier_rapide)
+  - [TFtd (en anglais)](https://en.wikipedia.org/wiki/Discrete-time_Fourier_transform)
+
+- en Anglais
+  - [An Interactive Guide To The Fourier Transform](https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/)
+  - [DFT on YouTube by Better Explained](https://www.youtube.com/watch?v=iN0VG9N2q0U&t=0s&index=77&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+  - [FT on YouTube by 3Blue1Brown](https://www.youtube.com/watch?v=spUNpyF58BY&t=0s&index=76&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+  - [FFT on YouTube by Simon Xu](https://www.youtube.com/watch?v=htCj9exbGo0&index=78&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&t=0s)

src/algorithms/math/fourier-transform/README.md

@@ -1,26 +1,29 @@
 # Fourier Transform
 
+_Read this in other languages:_
+[français](README.fr-FR.md).
+
 ## Definitions
 
-The **Fourier Transform** (**FT**) decomposes a function of time (a signal) into 
-the frequencies that make it up, in a way similar to how a musical chord can be 
+The **Fourier Transform** (**FT**) decomposes a function of time (a signal) into
+the frequencies that make it up, in a way similar to how a musical chord can be
 expressed as the frequencies (or pitches) of its constituent notes.
 
-The **Discrete Fourier Transform** (**DFT**) converts a finite sequence of 
-equally-spaced samples of a function into a same-length sequence of 
-equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a 
-complex-valued function of frequency. The interval at which the DTFT is sampled 
-is the reciprocal of the duration of the input sequence. An inverse DFT is a 
-Fourier series, using the DTFT samples as coefficients of complex sinusoids at 
-the corresponding DTFT frequencies. It has the same sample-values as the original 
-input sequence. The DFT is therefore said to be a frequency domain representation 
-of the original input sequence. If the original sequence spans all the non-zero 
-values of a function, its DTFT is continuous (and periodic), and the DFT provides 
-discrete samples of one cycle. If the original sequence is one cycle of a periodic 
+The **Discrete Fourier Transform** (**DFT**) converts a finite sequence of
+equally-spaced samples of a function into a same-length sequence of
+equally-spaced samples of the discrete-time Fourier transform (DTFT), which is a
+complex-valued function of frequency. The interval at which the DTFT is sampled
+is the reciprocal of the duration of the input sequence. An inverse DFT is a
+Fourier series, using the DTFT samples as coefficients of complex sinusoids at
+the corresponding DTFT frequencies. It has the same sample-values as the original
+input sequence. The DFT is therefore said to be a frequency domain representation
+of the original input sequence. If the original sequence spans all the non-zero
+values of a function, its DTFT is continuous (and periodic), and the DFT provides
+discrete samples of one cycle. If the original sequence is one cycle of a periodic
 function, the DFT provides all the non-zero values of one DTFT cycle.
 
 The Discrete Fourier transform transforms a sequence of `N` complex numbers:
-  
+
 {x<sub>n</sub>} = x<sub>0</sub>, x<sub>1</sub>, x<sub>2</sub> ..., x<sub>N-1</sub>
 
 into another sequence of complex numbers:
@@ -31,16 +34,16 @@ which is defined by:
 
 ![DFT](https://wikimedia.org/api/rest_v1/media/math/render/svg/1af0a78dc50bbf118ab6bd4c4dcc3c4ff8502223)
 
-The **Discrete-Time Fourier Transform** (**DTFT**) is a form of Fourier analysis 
-that is applicable to the uniformly-spaced samples of a continuous function. The 
+The **Discrete-Time Fourier Transform** (**DTFT**) is a form of Fourier analysis
+that is applicable to the uniformly-spaced samples of a continuous function. The
 term discrete-time refers to the fact that the transform operates on discrete data
-(samples) whose interval often has units of time. From only the samples, it 
-produces a function of frequency that is a periodic summation of the continuous 
+(samples) whose interval often has units of time. From only the samples, it
+produces a function of frequency that is a periodic summation of the continuous
 Fourier transform of the original continuous function.
 
 A **Fast Fourier Transform** (**FFT**) is an algorithm that samples a signal over
-a period of time (or space) and divides it into its frequency components. These 
-components are single sinusoidal oscillations at distinct frequencies each with 
+a period of time (or space) and divides it into its frequency components. These
+components are single sinusoidal oscillations at distinct frequencies each with
 their own amplitude and phase.
 
 This transformation is illustrated in Diagram below. Over the time period measured
@@ -50,22 +53,22 @@ View of a signal in the time and frequency domain:
 
 ![FFT](https://upload.wikimedia.org/wikipedia/commons/6/61/FFT-Time-Frequency-View.png)
 
-An FFT algorithm computes the discrete Fourier transform (DFT) of a sequence, or 
-its inverse (IFFT). Fourier analysis converts a signal from its original domain 
-to a representation in the frequency domain and vice versa. An FFT rapidly 
-computes such transformations by factorizing the DFT matrix into a product of 
-sparse (mostly zero) factors. As a result, it manages to reduce the complexity of 
-computing the DFT from O(n<sup>2</sup>), which arises if one simply applies the 
+An FFT algorithm computes the discrete Fourier transform (DFT) of a sequence, or
+its inverse (IFFT). Fourier analysis converts a signal from its original domain
+to a representation in the frequency domain and vice versa. An FFT rapidly
+computes such transformations by factorizing the DFT matrix into a product of
+sparse (mostly zero) factors. As a result, it manages to reduce the complexity of
+computing the DFT from O(n<sup>2</sup>), which arises if one simply applies the
 definition of DFT, to O(n log n), where n is the data size.
 
-Here a discrete Fourier analysis of a sum of cosine waves at 10, 20, 30, 40, 
+Here a discrete Fourier analysis of a sum of cosine waves at 10, 20, 30, 40,
 and 50 Hz:
 
 ![FFT](https://upload.wikimedia.org/wikipedia/commons/6/64/FFT_of_Cosine_Summation_Function.png)
 
 ## Explanation
 
-The Fourier Transform is one of deepest insights ever made. Unfortunately, the 
+The Fourier Transform is one of deepest insights ever made. Unfortunately, the
 meaning is buried within dense equations:
 
 ![](https://betterexplained.com/wp-content/plugins/wp-latexrender/pictures/45c088dbb767150fc0bacfeb49dd49e5.png)
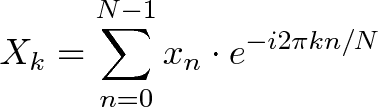
@@ -76,26 +79,26 @@ and
 
 Rather than jumping into the symbols, let's experience the key idea firsthand. Here's a plain-English metaphor:
 
-- *What does the Fourier Transform do?* Given a smoothie, it finds the recipe.
-- *How?* Run the smoothie through filters to extract each ingredient.
-- *Why?* Recipes are easier to analyze, compare, and modify than the smoothie itself.
-- *How do we get the smoothie back?* Blend the ingredients.
+- _What does the Fourier Transform do?_ Given a smoothie, it finds the recipe.
+- _How?_ Run the smoothie through filters to extract each ingredient.
+- _Why?_ Recipes are easier to analyze, compare, and modify than the smoothie itself.
+- _How do we get the smoothie back?_ Blend the ingredients.
 
 **Think With Circles, Not Just Sinusoids**
 
-The Fourier Transform is about circular paths (not 1-d sinusoids) and Euler's 
+The Fourier Transform is about circular paths (not 1-d sinusoids) and Euler's
 formula is a clever way to generate one:
 
 ![](https://betterexplained.com/wp-content/uploads/euler/equal_paths.png)
 
 Must we use imaginary exponents to move in a circle? Nope. But it's convenient
-and compact. And sure, we can describe our path as coordinated motion in two 
-dimensions (real and imaginary), but don't forget the big picture: we're just 
+and compact. And sure, we can describe our path as coordinated motion in two
+dimensions (real and imaginary), but don't forget the big picture: we're just
 moving in a circle.
 
 **Discovering The Full Transform**
 
-The big insight: our signal is just a bunch of time spikes! If we merge the 
+The big insight: our signal is just a bunch of time spikes! If we merge the
 recipes for each time spike, we should get the recipe for the full signal.
 
 The Fourier Transform builds the recipe frequency-by-frequency:
@@ -110,7 +113,7 @@ A few notes:
 - k = current frequency we're considering (0 Hertz up to N-1 Hertz)
 - X<sub>k</sub> = amount of frequency k in the signal (amplitude and phase, a complex number)
 - The 1/N factor is usually moved to the reverse transform (going from frequencies back to time). This is allowed, though I prefer 1/N in the forward transform since it gives the actual sizes for the time spikes. You can get wild and even use 1/sqrt(N) on both transforms (going forward and back creates the 1/N factor).
-- n/N is the percent of the time we've gone through. 2 * pi * k is our speed in radians / sec. e^-ix is our backwards-moving circular path. The combination is how far we've moved, for this speed and time.
+- n/N is the percent of the time we've gone through. 2 _ pi _ k is our speed in radians / sec. e^-ix is our backwards-moving circular path. The combination is how far we've moved, for this speed and time.
 - The raw equations for the Fourier Transform just say "add the complex numbers". Many programming languages cannot handle complex numbers directly, so you convert everything to rectangular coordinates and add those.
 
 Stuart Riffle has a great interpretation of the Fourier Transform:

src/algorithms/math/horner-method/README.md

@@ -0,0 +1,20 @@
+# Horner's Method
+
+In mathematics, Horner's method (or Horner's scheme) is an algorithm for polynomial evaluation. With this method, it is possible to evaluate a polynomial with only `n` additions and `n` multiplications. Hence, its storage requirements are `n` times the number of bits of `x`.
+
+Horner's method can be based on the following identity:
+
+![Horner's rule](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a576e42d875496f8b0f0dda5ebff7c2415532e4)
+
+This identity is called _Horner's rule_.
+
+To solve the right part of the identity above, for a given `x`, we start by iterating through the polynomial from the inside out, accumulating each iteration result. After `n` iterations, with `n` being the order of the polynomial, the accumulated result gives us the polynomial evaluation. 
+
+**Using the polynomial:**
+`4 * x^4 + 2 * x^3 + 3 * x^2 + x^1 + 3`, a traditional approach to evaluate it at `x = 2`, could be representing it as an array `[3, 1, 3, 2, 4]` and iterate over it saving each iteration value at an accumulator, such as `acc += pow(x=2, index) * array[index]`. In essence, each power of a number (`pow`) operation is `n-1` multiplications. So, in this scenario, a total of `14` operations would have happened, composed of `4` additions, `5` multiplications, and `5` pows (we're assuming that each power is calculated by repeated multiplication).
+
+Now, **using the same scenario but with Horner's rule**, the polynomial can be re-written as `x * (x * (x * (4 * x + 2) + 3) + 1) + 3`, representing it as `[4, 2, 3, 1, 3]` it is possible to save the first iteration as `acc = arr[0] * (x=2) + arr[1]`, and then finish iterations for `acc *= (x=2) + arr[index]`. In the same scenario but using Horner's rule, a total of `10` operations would have happened, composed of only `4` additions and `4` multiplications.
+
+## References
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Horner%27s_method)

src/algorithms/math/horner-method/__test__/classicPolynome.test.js

@@ -0,0 +1,14 @@
+import classicPolynome from '../classicPolynome';
+
+describe('classicPolynome', () => {
+  it('should evaluate the polynomial for the specified value of x correctly', () => {
+    expect(classicPolynome([8], 0.1)).toBe(8);
+    expect(classicPolynome([2, 4, 2, 5], 0.555)).toBe(7.68400775);
+    expect(classicPolynome([2, 4, 2, 5], 0.75)).toBe(9.59375);
+    expect(classicPolynome([1, 1, 1, 1, 1], 1.75)).toBe(20.55078125);
+    expect(classicPolynome([15, 3.5, 0, 2, 1.42, 0.41], 0.315)).toBe(1.1367300651406251);
+    expect(classicPolynome([0, 0, 2.77, 1.42, 0.41], 1.35)).toBe(7.375325000000001);
+    expect(classicPolynome([0, 0, 2.77, 1.42, 2.3311], 1.35)).toBe(9.296425000000001);
+    expect(classicPolynome([2, 0, 0, 5.757, 5.31412, 12.3213], 3.141)).toBe(697.2731167035034);
+  });
+});

src/algorithms/math/horner-method/__test__/hornerMethod.test.js

@@ -0,0 +1,21 @@
+import hornerMethod from '../hornerMethod';
+import classicPolynome from '../classicPolynome';
+
+describe('hornerMethod', () => {
+  it('should evaluate the polynomial for the specified value of x correctly', () => {
+    expect(hornerMethod([8], 0.1)).toBe(8);
+    expect(hornerMethod([2, 4, 2, 5], 0.555)).toBe(7.68400775);
+    expect(hornerMethod([2, 4, 2, 5], 0.75)).toBe(9.59375);
+    expect(hornerMethod([1, 1, 1, 1, 1], 1.75)).toBe(20.55078125);
+    expect(hornerMethod([15, 3.5, 0, 2, 1.42, 0.41], 0.315)).toBe(1.136730065140625);
+    expect(hornerMethod([0, 0, 2.77, 1.42, 0.41], 1.35)).toBe(7.375325000000001);
+    expect(hornerMethod([0, 0, 2.77, 1.42, 2.3311], 1.35)).toBe(9.296425000000001);
+    expect(hornerMethod([2, 0, 0, 5.757, 5.31412, 12.3213], 3.141)).toBe(697.2731167035034);
+  });
+
+  it('should evaluate the same polynomial value as classical approach', () => {
+    expect(hornerMethod([8], 0.1)).toBe(classicPolynome([8], 0.1));
+    expect(hornerMethod([2, 4, 2, 5], 0.555)).toBe(classicPolynome([2, 4, 2, 5], 0.555));
+    expect(hornerMethod([2, 4, 2, 5], 0.75)).toBe(classicPolynome([2, 4, 2, 5], 0.75));
+  });
+});

src/algorithms/math/horner-method/classicPolynome.js

@@ -0,0 +1,16 @@
+/**
+ * Returns the evaluation of a polynomial function at a certain point.
+ * Uses straightforward approach with powers.
+ *
+ * @param {number[]} coefficients - i.e. [4, 3, 2] for (4 * x^2 + 3 * x + 2)
+ * @param {number} xVal
+ * @return {number}
+ */
+export default function classicPolynome(coefficients, xVal) {
+  return coefficients.reverse().reduce(
+    (accumulator, currentCoefficient, index) => {
+      return accumulator + currentCoefficient * (xVal ** index);
+    },
+    0,
+  );
+}

src/algorithms/math/horner-method/hornerMethod.js

@@ -0,0 +1,16 @@
+/**
+ * Returns the evaluation of a polynomial function at a certain point.
+ * Uses Horner's rule.
+ *
+ * @param {number[]} coefficients - i.e. [4, 3, 2] for (4 * x^2 + 3 * x + 2)
+ * @param {number} xVal
+ * @return {number}
+ */
+export default function hornerMethod(coefficients, xVal) {
+  return coefficients.reduce(
+    (accumulator, currentCoefficient) => {
+      return accumulator * xVal + currentCoefficient;
+    },
+    0,
+  );
+}

src/algorithms/math/prime-factors/README.md

@@ -0,0 +1,34 @@
+# Prime Factors
+
+**Prime number** is a whole number greater than `1` that **cannot** be made by multiplying other whole numbers. The first few prime numbers are: `2`, `3`, `5`, `7`, `11`, `13`, `17`, `19` and so on.
+
+If we **can** make it by multiplying other whole numbers it is a **Composite Number**.
+
+![Composite numbers](https://www.mathsisfun.com/numbers/images/prime-composite.svg)
+
+_Image source: [Math is Fun](https://www.mathsisfun.com/prime-factorization.html)_
+
+**Prime factors** are those [prime numbers](https://en.wikipedia.org/wiki/Prime_number) which multiply together to give the original number. For example `39` will have prime factors of `3` and `13` which are also prime numbers. Another example is `15` whose prime factors are `3` and `5`.
+
+![Factors](https://www.mathsisfun.com/numbers/images/factor-2x3.svg)
+
+_Image source: [Math is Fun](https://www.mathsisfun.com/prime-factorization.html)_
+
+## Finding the prime factors and their count accurately
+
+The approach is to keep on dividing the natural number `n` by indexes from `i = 2` to `i = n` (by prime indexes only). The value of `n` is being overridden by `(n / i)` on each iteration.
+
+The time complexity till now is `O(n)` in the worst case scenario since the loop runs from index `i = 2` to `i = n`. This time complexity can be reduced from `O(n)` to `O(sqrt(n))`. The optimisation is achievable when loop runs from `i = 2` to `i = sqrt(n)`. Now, we go only till `O(sqrt(n))` because when `i` becomes greater than `sqrt(n)`, we have the confirmation that there is no index `i` left which can divide `n` completely other than `n` itself.
+
+## Hardy-Ramanujan formula for approximate calculation of prime-factor count
+
+In 1917, a theorem was formulated by G.H Hardy and Srinivasa Ramanujan which states that the normal order of the number `ω(n)` of distinct prime factors of a number `n` is `log(log(n))`.
+
+Roughly speaking, this means that most numbers have about this number of distinct prime factors.
+
+## References
+
+- [Prime numbers on Math is Fun](https://www.mathsisfun.com/prime-factorization.html)
+- [Prime numbers on Wikipedia](https://en.wikipedia.org/wiki/Prime_number)
+- [Hardy–Ramanujan theorem on Wikipedia](https://en.wikipedia.org/wiki/Hardy%E2%80%93Ramanujan_theorem)
+- [Prime factorization of a number on Youtube](https://www.youtube.com/watch?v=6PDtgHhpCHo&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=82)

src/algorithms/math/prime-factors/__test__/primeFactors.test.js

@@ -0,0 +1,87 @@
+import {
+  primeFactors,
+  hardyRamanujan,
+} from '../primeFactors';
+
+/**
+ * Calculates the error between exact and approximate prime factor counts.
+ * @param {number} exactCount
+ * @param {number} approximateCount
+ * @returns {number} - approximation error (percentage).
+ */
+function approximationError(exactCount, approximateCount) {
+  return (Math.abs((exactCount - approximateCount) / exactCount) * 100);
+}
+
+describe('primeFactors', () => {
+  it('should find prime factors', () => {
+    expect(primeFactors(1)).toEqual([]);
+    expect(primeFactors(2)).toEqual([2]);
+    expect(primeFactors(3)).toEqual([3]);
+    expect(primeFactors(4)).toEqual([2, 2]);
+    expect(primeFactors(14)).toEqual([2, 7]);
+    expect(primeFactors(40)).toEqual([2, 2, 2, 5]);
+    expect(primeFactors(54)).toEqual([2, 3, 3, 3]);
+    expect(primeFactors(100)).toEqual([2, 2, 5, 5]);
+    expect(primeFactors(156)).toEqual([2, 2, 3, 13]);
+    expect(primeFactors(273)).toEqual([3, 7, 13]);
+    expect(primeFactors(300)).toEqual([2, 2, 3, 5, 5]);
+    expect(primeFactors(980)).toEqual([2, 2, 5, 7, 7]);
+    expect(primeFactors(1000)).toEqual([2, 2, 2, 5, 5, 5]);
+    expect(primeFactors(52734)).toEqual([2, 3, 11, 17, 47]);
+    expect(primeFactors(343434)).toEqual([2, 3, 7, 13, 17, 37]);
+    expect(primeFactors(456745)).toEqual([5, 167, 547]);
+    expect(primeFactors(510510)).toEqual([2, 3, 5, 7, 11, 13, 17]);
+    expect(primeFactors(8735463)).toEqual([3, 3, 11, 88237]);
+    expect(primeFactors(873452453)).toEqual([149, 1637, 3581]);
+  });
+
+  it('should give approximate prime factors count using Hardy-Ramanujan theorem', () => {
+    expect(hardyRamanujan(2)).toBeCloseTo(-0.366, 2);
+    expect(hardyRamanujan(4)).toBeCloseTo(0.326, 2);
+    expect(hardyRamanujan(40)).toBeCloseTo(1.305, 2);
+    expect(hardyRamanujan(156)).toBeCloseTo(1.6193, 2);
+    expect(hardyRamanujan(980)).toBeCloseTo(1.929, 2);
+    expect(hardyRamanujan(52734)).toBeCloseTo(2.386, 2);
+    expect(hardyRamanujan(343434)).toBeCloseTo(2.545, 2);
+    expect(hardyRamanujan(456745)).toBeCloseTo(2.567, 2);
+    expect(hardyRamanujan(510510)).toBeCloseTo(2.575, 2);
+    expect(hardyRamanujan(8735463)).toBeCloseTo(2.771, 2);
+    expect(hardyRamanujan(873452453)).toBeCloseTo(3.024, 2);
+  });
+
+  it('should give correct deviation between exact and approx counts', () => {
+    expect(approximationError(primeFactors(2).length, hardyRamanujan(2)))
+      .toBeCloseTo(136.651, 2);
+
+    expect(approximationError(primeFactors(4).length, hardyRamanujan(2)))
+      .toBeCloseTo(118.325, 2);
+
+    expect(approximationError(primeFactors(40).length, hardyRamanujan(2)))
+      .toBeCloseTo(109.162, 2);
+
+    expect(approximationError(primeFactors(156).length, hardyRamanujan(2)))
+      .toBeCloseTo(109.162, 2);
+
+    expect(approximationError(primeFactors(980).length, hardyRamanujan(2)))
+      .toBeCloseTo(107.330, 2);
+
+    expect(approximationError(primeFactors(52734).length, hardyRamanujan(52734)))
+      .toBeCloseTo(52.274, 2);
+
+    expect(approximationError(primeFactors(343434).length, hardyRamanujan(343434)))
+      .toBeCloseTo(57.578, 2);
+
+    expect(approximationError(primeFactors(456745).length, hardyRamanujan(456745)))
+      .toBeCloseTo(14.420, 2);
+
+    expect(approximationError(primeFactors(510510).length, hardyRamanujan(510510)))
+      .toBeCloseTo(63.201, 2);
+
+    expect(approximationError(primeFactors(8735463).length, hardyRamanujan(8735463)))
+      .toBeCloseTo(30.712, 2);
+
+    expect(approximationError(primeFactors(873452453).length, hardyRamanujan(873452453)))
+      .toBeCloseTo(0.823, 2);
+  });
+});

src/algorithms/math/prime-factors/primeFactors.js

@@ -0,0 +1,42 @@
+/**
+ * Finds prime factors of a number.
+ *
+ * @param {number} n - the number that is going to be split into prime factors.
+ * @returns {number[]} - array of prime factors.
+ */
+export function primeFactors(n) {
+  // Clone n to avoid function arguments override.
+  let nn = n;
+
+  // Array that stores the all the prime factors.
+  const factors = [];
+
+  // Running the loop till sqrt(n) instead of n to optimise time complexity from O(n) to O(sqrt(n)).
+  for (let factor = 2; factor <= Math.sqrt(nn); factor += 1) {
+    // Check that factor divides n without a reminder.
+    while (nn % factor === 0) {
+      // Overriding the value of n.
+      nn /= factor;
+      // Saving the factor.
+      factors.push(factor);
+    }
+  }
+
+  // The ultimate reminder should be a last prime factor,
+  // unless it is not 1 (since 1 is not a prime number).
+  if (nn !== 1) {
+    factors.push(nn);
+  }
+
+  return factors;
+}
+
+/**
+ * Hardy-Ramanujan approximation of prime factors count.
+ *
+ * @param {number} n
+ * @returns {number} - approximate number of prime factors.
+ */
+export function hardyRamanujan(n) {
+  return Math.log(Math.log(n));
+}

src/algorithms/sorting/merge-sort/MergeSort.js

@@ -24,36 +24,37 @@ export default class MergeSort extends Sort {
   }
 
   mergeSortedArrays(leftArray, rightArray) {
-    let sortedArray = [];
+    const sortedArray = [];
 
-    // In case if arrays are not of size 1.
-    while (leftArray.length && rightArray.length) {
-      let minimumElement = null;
+    // Use array pointers to exclude old elements after they have been added to the sorted array.
+    let leftIndex = 0;
+    let rightIndex = 0;
 
-      // Find minimum element of two arrays.
-      if (this.comparator.lessThanOrEqual(leftArray[0], rightArray[0])) {
-        minimumElement = leftArray.shift();
+    while (leftIndex < leftArray.length && rightIndex < rightArray.length) {
+      let minElement = null;
+
+      // Find the minimum element between the left and right array.
+      if (this.comparator.lessThanOrEqual(leftArray[leftIndex], rightArray[rightIndex])) {
+        minElement = leftArray[leftIndex];
+        // Increment index pointer to the right
+        leftIndex += 1;
       } else {
-        minimumElement = rightArray.shift();
+        minElement = rightArray[rightIndex];
+        // Increment index pointer to the right
+        rightIndex += 1;
       }
 
+      // Add the minimum element to the sorted array.
+      sortedArray.push(minElement);
+
       // Call visiting callback.
-      this.callbacks.visitingCallback(minimumElement);
-
-      // Push the minimum element of two arrays to the sorted array.
-      sortedArray.push(minimumElement);
+      this.callbacks.visitingCallback(minElement);
     }
 
-    // If one of two array still have elements we need to just concatenate
-    // this element to the sorted array since it is already sorted.
-    if (leftArray.length) {
-      sortedArray = sortedArray.concat(leftArray);
-    }
-
-    if (rightArray.length) {
-      sortedArray = sortedArray.concat(rightArray);
-    }
-
-    return sortedArray;
+    // There will be elements remaining from either the left OR the right
+    // Concatenate the remaining elements into the sorted array
+    return sortedArray
+      .concat(leftArray.slice(leftIndex))
+      .concat(rightArray.slice(rightIndex));
   }
 }

src/algorithms/tree/breadth-first-search/__test__/breadthFirstSearch.test.js

@@ -2,7 +2,7 @@ import BinaryTreeNode from '../../../../data-structures/tree/BinaryTreeNode';
 import breadthFirstSearch from '../breadthFirstSearch';
 
 describe('breadthFirstSearch', () => {
-  it('should perform DFS operation on tree', () => {
+  it('should perform BFS operation on tree', () => {
     const nodeA = new BinaryTreeNode('A');
     const nodeB = new BinaryTreeNode('B');
     const nodeC = new BinaryTreeNode('C');

src/algorithms/uncategorized/rain-terraces/bfRainTerraces.js

@@ -25,7 +25,7 @@ export default function bfRainTerraces(terraces) {
     if (terraceBoundaryLevel > terraces[terraceIndex]) {
       // Terrace will be able to store the water if the lowest of two left and right highest
       // terraces are still higher than the current one.
-      waterAmount += Math.min(leftHighestLevel, rightHighestLevel) - terraces[terraceIndex];
+      waterAmount += terraceBoundaryLevel - terraces[terraceIndex];
     }
   }
 

src/data-structures/doubly-linked-list/README.ko-KR.md

@@ -0,0 +1,107 @@
+# Doubly Linked List
+
+_Read this in other languages:_
+[_Русский_](README.ru-RU.md),
+[_简体中文_](README.zh-CN.md),
+[_日本語_](README.ja-JP.md),
+[_Português_](README.pt-BR.md)
+
+컴퓨터공학에서 **이중 연결 리스트**는 순차적으로 링크된 노드라는 레코드 세트로 구성된 링크된 데이터 구조입니다.
+각 노드에는 링크라고 하는 두 개의 필드가 있으며, 노드 순서에서 이전 노드와 다음 노드에 대한 참조를 가집니다.
+시작 및 종료 노드의 이전 및 다음 링크는 각각 리스트의 순회를 용이하게 하기 위해서 일종의 종결자 (일반적으로 센티넬노드 또는 null)를 나타냅니다.
+센티넬 노드가 하나만 있으면, 목록이 센티넬 노드를 통해서 원형으로 연결됩니다.
+동일한 데이터 항목으로 구성되어 있지만, 반대 순서로 두 개의 단일 연결 리스트로 개념화 할 수 있습니다.
+
+![이중 연결 리스트](https://upload.wikimedia.org/wikipedia/commons/5/5e/Doubly-linked-list.svg)
+
+두 개의 노드 링크를 사용하면 어느 방향으로든 리스트를 순회할 수 있습니다.
+이중 연결 리스트에서 노드를 추가하거나 제거하려면, 단일 연결 리스트에서 동일한 작업보다 더 많은 링크를 변경해야 하지만, 첫 번째 노드 이외의 노드인 경우 작업을 추적할 필요가 없으므로 작업이 더 단순해져 잠재적으로 더 효율적입니다.
+리스트 순회 중 이전 노드 또는 링크를 수정할 수 있도록 이전 노드를 찾기 위해 리스트를 순회할 필요가 없습니다.
+
+## 기본 동작을 위한 Pseudocode
+
+### 삽입
+
+```text
+Add(value)
+  Pre: value는 리스트에 추가하고자 하는 값
+  Post: value는 목록의 끝에 배치됨
+  n ← node(value)
+  if head = ø
+    head ← n
+    tail ← n
+  else
+    n.previous ← tail
+    tail.next ← n
+    tail ← n
+  end if
+end Add
+```
+    
+### 삭제
+
+```text
+Remove(head, value)
+  Pre: head는 리스트의 앞단에 위치
+       value는 리스트에서 제거하고자 하는 값
+  Post: value가 리스트에서 제거되면 true; 아니라면 false;
+  if head = ø
+    return false
+  end if
+  if value = head.value
+    if head = tail
+      head ← ø
+      tail ← ø
+    else
+      head ← head.next
+      head.previous ← ø
+    end if
+    return true
+  end if
+  n ← head.next
+  while n = ø and value !== n.value
+    n ← n.next
+  end while
+  if n = tail
+    tail ← tail.previous
+    tail.next ← ø
+    return true
+  else if n = ø
+    n.previous.next ← n.next
+    n.next.previous ← n.previous
+    return true
+  end if
+  return false
+end Remove
+```
+    
+### 역순회
+
+```text
+ReverseTraversal(tail)
+  Pre: tail은 리스트에서 순회하고자 하는 노드
+  Post: 리스트가 역순으로 순회됨
+  n ← tail
+  while n = ø
+    yield n.value
+    n ← n.previous
+  end while
+end Reverse Traversal
+```
+    
+## 복잡도
+
+## 시간 복잡도
+
+| Access    | Search    | Insertion | Deletion  |
+| :-------: | :-------: | :-------: | :-------: |
+| O(n)      | O(n)      | O(1)      | O(n)      |
+
+### 공간 복잡도
+
+O(n)
+
+## 참고
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Doubly_linked_list)
+- [YouTube](https://www.youtube.com/watch?v=JdQeNxWCguQ&t=7s&index=72&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)

src/data-structures/doubly-linked-list/README.md

@@ -5,13 +5,14 @@ _Read this in other languages:_
 [_简体中文_](README.zh-CN.md),
 [_日本語_](README.ja-JP.md),
 [_Português_](README.pt-BR.md)
+[_한국어_](README.ko-KR.md)
 
 In computer science, a **doubly linked list** is a linked data structure that 
 consists of a set of sequentially linked records called nodes. Each node contains 
 two fields, called links, that are references to the previous and to the next 
 node in the sequence of nodes. The beginning and ending nodes' previous and next 
 links, respectively, point to some kind of terminator, typically a sentinel 
-node or null, to facilitate traversal of the list. If there is only one 
+node or null, to facilitate the traversal of the list. If there is only one 
 sentinel node, then the list is circularly linked via the sentinel node. It can 
 be conceptualized as two singly linked lists formed from the same data items, 
 but in opposite sequential orders.

src/data-structures/hash-table/HashTable.js

@@ -105,4 +105,17 @@ export default class HashTable {
   getKeys() {
     return Object.keys(this.keys);
   }
+
+  /**
+   * Gets the list of all the stored values in the hash table.
+   *
+   * @return {*[]}
+   */
+  getValues() {
+    return this.buckets.reduce((values, bucket) => {
+      const bucketValues = bucket.toArray()
+        .map((linkedListNode) => linkedListNode.value.value);
+      return values.concat(bucketValues);
+    }, []);
+  }
 }

src/data-structures/hash-table/__test__/HashTable.test.js

@@ -86,4 +86,32 @@ describe('HashTable', () => {
     expect(hashTable.has('b')).toBe(true);
     expect(hashTable.has('x')).toBe(false);
   });
+
+  it('should get all the values', () => {
+    const hashTable = new HashTable(3);
+
+    hashTable.set('a', 'alpha');
+    hashTable.set('b', 'beta');
+    hashTable.set('c', 'gamma');
+
+    expect(hashTable.getValues()).toEqual(['gamma', 'alpha', 'beta']);
+  });
+
+  it('should get all the values from empty hash table', () => {
+    const hashTable = new HashTable();
+    expect(hashTable.getValues()).toEqual([]);
+  });
+
+  it('should get all the values in case of hash collision', () => {
+    const hashTable = new HashTable(3);
+
+    // Keys `ab` and `ba` in current implementation should result in one hash (one bucket).
+    // We need to make sure that several items from one bucket will be serialized.
+    hashTable.set('ab', 'one');
+    hashTable.set('ba', 'two');
+
+    hashTable.set('ac', 'three');
+
+    expect(hashTable.getValues()).toEqual(['one', 'two', 'three']);
+  });
 });

src/data-structures/linked-list/README.ko-KR.md

@@ -0,0 +1,149 @@
+# 링크드 리스트
+
+_Read this in other languages:_
+[_简体中文_](README.zh-CN.md),
+[_Русский_](README.ru-RU.md),
+[_日本語_](README.ja-JP.md),
+[_Português_](README.pt-BR.md)
+
+컴퓨터과학에서, **링크드 리스트**는 데이터 요소의 선형 집합이며, 이 집합에서 논리적 저장 순서는 메모리의 물리적 저장 순서와 일치하지 않습니다. 그 대신, 각각의 원소들은 자기 자신 다음의 원소를 가리킵니다. **링크드 리스트**는 순서를 표현하는 노드들의 집합으로 이루어져 있습니다. 간단하게, 각각의 노드들은 데이터와 다음 순서의 노드를 가리키는 레퍼런스로 이루어져 있습니다. (링크라고 부릅니다.) 이 자료구조는 순회하는 동안 순서에 상관없이 효율적인 삽입이나 삭제가 가능합니다. 더 복잡한 변형은 추가적인 링크를 더해, 임의의 원소 참조로부터 효율적인 삽입과 삭제를 가능하게 합니다. 링크드 리스트의 단점은 접근 시간이 선형이라는 것이고, 병렬처리도 하지 못합니다. 임의 접근처럼 빠른 접근은 불가능합니다. 링크드 리스트에 비해 배열이 더 나은 캐시 지역성을 가지고 있습니다.
+
+![링크드 리스트](https://upload.wikimedia.org/wikipedia/commons/6/6d/Singly-linked-list.svg)
+
+## 기본 연산에 대한 수도코드
+
+### 삽입
+
+```text
+Add(value)
+  Pre: 리스트에 추가할 값
+  Post: 리스트의 맨 마지막에 있는 값
+  n ← node(value)
+  if head = ø
+    head ← n
+    tail ← n
+  else
+    tail.next ← n
+    tail ← n
+  end if
+end Add
+```
+
+```text
+Prepend(value)
+ Pre: 리스트에 추가할 값
+ Post: 리스트의 맨 앞에 있는 값
+ n ← node(value)
+ n.next ← head
+ head ← n
+ if tail = ø
+   tail ← n
+ end
+end Prepend
+```
+
+### 탐색
+
+```text
+Contains(head, value)
+  Pre: head는 리스트에서 맨 앞 노드
+       value는 찾고자 하는 값
+  Post: 항목이 링크드 리스트에 있으면 true;
+        없으면 false
+  n ← head
+  while n != ø and n.value != value
+    n ← n.next
+  end while
+  if n = ø
+    return false
+  end if
+  return true
+end Contains
+```
+    
+### 삭제
+
+```text
+Remove(head, value)
+  Pre: head는 리스트에서 맨 앞 노드
+       value는 삭제하고자 하는 값
+  Post: 항목이 링크드 리스트에서 삭제되면 true;
+        없으면 false
+  if head = ø
+    return false
+  end if
+  n ← head
+  if n.value = value
+    if head = tail
+      head ← ø
+      tail ← ø
+    else
+      head ← head.next
+    end if
+    return true
+  end if
+  while n.next != ø and n.next.value != value
+    n ← n.next
+  end while
+  if n.next != ø
+    if n.next = tail
+      tail ← n
+    end if
+    n.next ← n.next.next
+    return true
+  end if
+  return false
+end Remove
+```
+
+### 순회
+
+```text
+Traverse(head)
+  Pre: head는 리스트에서 맨 앞 노드
+  Post: 순회된 항목들
+  n ← head
+  while n != ø
+    yield n.value
+    n ← n.next
+  end while
+end Traverse
+```
+
+### 역순회
+
+```text
+ReverseTraversal(head, tail)
+  Pre: 같은 리스트에 들어 있는 맨 앞, 맨 뒤 노드
+  Post: 역순회된 항목들
+  if tail != ø
+    curr ← tail
+    while curr != head
+      prev ← head
+      while prev.next != curr
+        prev ← prev.next
+      end while
+      yield curr.value
+      curr ← prev
+    end while
+   yield curr.value
+  end if
+end ReverseTraversal
+```
+
+## 복잡도
+
+### 시간 복잡도
+
+|  접근   |  탐색   |  삽입   |  삭제   |
+| :---: | :---: | :---: | :---: |
+| O(n)  | O(n)  | O(1)  | O(1)  |
+
+### 공간 복잡도
+
+O(n)
+
+## 참조
+
+- [Wikipedia](https://en.wikipedia.org/wiki/Linked_list)
+- [YouTube](https://www.youtube.com/watch?v=njTh_OwMljA&index=2&t=1s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)

src/data-structures/linked-list/README.md

@@ -4,7 +4,8 @@ _Read this in other languages:_
 [_简体中文_](README.zh-CN.md),
 [_Русский_](README.ru-RU.md),
 [_日本語_](README.ja-JP.md),
-[_Português_](README.pt-BR.md)
+[_Português_](README.pt-BR.md),
+[_한국어_](README.ko-KR.md)
 
 In computer science, a **linked list** is a linear collection 
 of data elements, in which linear order is not given by 

src/data-structures/tree/red-black-tree/RedBlackTree.js

@@ -155,7 +155,7 @@ export default class RedBlackTree extends BinarySearchTree {
       parentNode.parent = null;
     }
 
-    // Swap colors of granParent and parent nodes.
+    // Swap colors of grandParentNode and parentNode.
     this.swapNodeColors(parentNode, grandParentNode);
 
     // Return new root node.

src/data-structures/trie/README.ru-RU.md

@@ -2,7 +2,7 @@
 
 **Префиксное дерево** (также бор, луч, нагруженное или суффиксное дерево) в информатике - упорядоченная древовидная
 структура данных, которая используется для хранения динамических множеств или ассоциативных массивов, где
-ключём обычно выступают строки. Дерево называется префиксным, потому что поиск осуществляется по префиксам.
+ключом обычно выступают строки. Дерево называется префиксным, потому что поиск осуществляется по префиксам.
 
 В отличие от бинарного дерева, узлы не содержат ключи, соответствующие узлу. Представляет собой корневое дерево, каждое
 ребро которого помечено каким-то символом так, что для любого узла все рёбра, соединяющие этот узел с его сыновьями,