# JavaScript Algorytmy i Struktury Danych

[![Build Status](https://travis-ci.org/trekhleb/javascript-algorithms.svg?branch=master)](https://travis-ci.org/trekhleb/javascript-algorithms)
[![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)

To repozytorium zawiera wiele przykładów JavaScript opartych na 
znanych algorytmach i strukturach danych.

Każdy algorytm i struktura danych zawiera osobny plik README
wraz z powiązanymi wyjaśnieniami i odnośnikami do dalszego czytania 
(włącznie z tymi do YouTube videos).

_Read this in other languages:_
[_English_](https://github.com/trekhleb/javascript-algorithms/)
[_简体中文_](README.zh-CN.md),
[_繁體中文_](README.zh-TW.md),
[_한국어_](README.ko-KR.md),
[_日本語_](README.ja-JP.md),
[_Français_](README.fr-FR.md),
[_Español_](README.es-ES.md),
[_Português_](README.pt-BR.md),
[_Русский_](README.ru-RU.md),
[_Türk_](README.tr-TR.md),
[_Italiana_](README.it-IT.md)

## Struktury Danych

Struktura danych to sposób uporządkowania i przechowywania informacji w 
komputerze żeby mogłaby być sprawnie dostępna i efektywnie zmodyfikowana.
Dokładniej, struktura danych jest zbiorem wartości danych, relacjami 
pomiędzy nimi, zadaniami lub działaniami, które mogą dotyczyć danych. 

`B` - Początkujący, `A` - Zaawansowany

* `B` [Lista](src/data-structures/linked-list)
* `B` [Lista Dwukierunkowa](src/data-structures/doubly-linked-list)
* `B` [Kolejka](src/data-structures/queue)
* `B` [Stos](src/data-structures/stack)
* `B` [Tabela Skrótu](src/data-structures/hash-table)
* `B` [Sterta](src/data-structures/heap)
* `B` [Kolejka Priorytetowa](src/data-structures/priority-queue)
* `A` [Trie](src/data-structures/trie)
* `A` [Drzewo](src/data-structures/tree)
  * `A` [Wyszukiwanie Binarne](src/data-structures/tree/binary-search-tree)
  * `A` [AVL Drzewo](src/data-structures/tree/avl-tree)
  * `A` [Drzewa czerwono-czarne](src/data-structures/tree/red-black-tree)
  * `A` [Drzewo Segmentu](src/data-structures/tree/segment-tree) - z przykładami zapytań o min / max / sumie sum
  * `A` [Drzewo Fenwicka](src/data-structures/tree/fenwick-tree) (Drzewo Indeksowane Binarnie)
* `A` [Graf](src/data-structures/graph) (zarówno skierowane i nieukierunkowane)
* `A` [Rozłączny Zestaw](src/data-structures/disjoint-set)
* `A` [Filtr Blooma](src/data-structures/bloom-filter)

## Algorytmy

Algorytm jest to skończony ciąg jasno zdefiniowanych czynności, koniecznych 
do wykonania pewnego rodzaju zadań. Sposób postępowania prowadzący do 
rozwiązania problemu.

`B` - Początkujący, `A` - Zaawansowany

### Algorytmy według tematu

* **Matematyka**
  * `B` [Manipulacja Bitami](src/algorithms/math/bits) - ustaw / uzyskaj / aktualizuj / usuwaj bity, mnożenie / dzielenie przez dwa, tworzenie negatywów itp.
  * `B` [Silna](src/algorithms/math/factorial) 
  * `B` [Ciąg Fibonacciego](src/algorithms/math/fibonacci)
  * `B` [Test Pierwszorzędności](src/algorithms/math/primality-test) (metoda podziału na próby)
  * `B` [Algorytm Euclideana](src/algorithms/math/euclidean-algorithm) - obliczyć Największy Wspólny Dzielnik (GCD)
  * `B` [Najmniejsza Wspólna Wielokrotność](src/algorithms/math/least-common-multiple) (LCM)
  * `B` [Sito Eratosthenes-a](src/algorithms/math/sieve-of-eratosthenes) - znajdowanie wszystkich liczb pierwszych do określonego limitu
  * `B` [Jest Potęgą Dwójki](src/algorithms/math/is-power-of-two) - sprawdź, czy liczba jest potęgą dwóch (algorytmy naiwne i bitowe)
  * `B` [Trójkąt Pascala](src/algorithms/math/pascal-triangle)
  * `A` [Partycja Całkowita](src/algorithms/math/integer-partition)
  * `A` [Algorytm Liu Huia](src/algorithms/math/liu-hui) - przybliżone obliczenia na podstawie N-gonów
* **Zestawy**
  * `B` [Produkt Kartezyjny](src/algorithms/sets/cartesian-product) - wynik wielu zestawów
  * `B` [Przetasowanie Fisher Yates-a](src/algorithms/sets/fisher-yates) - losowa permutacja kończącej się serii
  * `A` [Zestaw Zasilający](src/algorithms/sets/power-set) - podzbiór wszystkich serii
  * `A` [Permutacje](src/algorithms/sets/permutations) (z albo bez powtórzeń)
  * `A` [Kombinacje](src/algorithms/sets/combinations) (z albo bez powtórzeń)
  * `A` [Najdłuższa Wspólna Podsekwencja](src/algorithms/sets/longest-common-subsequence) (LCS)
  * `A` [Najdłuższa Wzrostająca Podsekwencja](src/algorithms/sets/longest-increasing-subsequence)
  * `A` [Najkrótsza Wspólna Supersekwencja](src/algorithms/sets/shortest-common-supersequence) (SCS)
  * `A` [Problem Knapsacka](src/algorithms/sets/knapsack-problem) - "0/1" i "Rozwiązany" 
  * `A` [Maksymalna Podtablica](src/algorithms/sets/maximum-subarray) - "Metoda Siłowa" i "Dynamiczne Programowanie" (Kadane-a) wersje
  * `A` [Suma Kombinacji](src/algorithms/sets/combination-sum) - 
znajdź wszystkie kombinacje, które tworzą określoną sumę
* **Łańcuchy**
  * `B` [Odległość Hamminga](src/algorithms/string/hamming-distance) - liczba pozycji, w których symbole są różne
  * `A` [Odległość Levenshteina](src/algorithms/string/levenshtein-distance) - minimalna odległość edycji między dwiema sekwencjami
  * `A` [Algorytm Knuth–Morris–Pratta](src/algorithms/string/knuth-morris-pratt) (Algorytm KMP) - dopasowywanie wzorców (dopasowywanie wzorców)
  * `A` [Algorytm Z](src/algorithms/string/z-algorithm) - szukanie podłańcucha(dopasowywanie wzorców)
  * `A` [Algorytm Rabin Karpa](src/algorithms/string/rabin-karp) - szukanie podłańcucha
  * `A` [Najdłuższa Wspólna Podłańcucha](src/algorithms/string/longest-common-substring)
  * `A` [Dopasowanie Wyrażeń Regularnych](src/algorithms/string/regular-expression-matching)
* **Szukanie**
  * `B` [Wyszukiwanie Liniowe](src/algorithms/search/linear-search)
  * `B` [Jump Search](src/algorithms/search/jump-search) (lub Przeszukiwanie Bloku) - szukaj w posortowanej tablicy
  * `B` [Wyszukiwanie Binarne](src/algorithms/search/binary-search) - szukaj w posortowanej tablicy
  * `B` [Wyszukiwanie Interpolacyjne](src/algorithms/search/interpolation-search) - szukaj w równomiernie rozłożonej, posortowanej tablicy
* **Sortowanie**
  * `B` [Sortowanie bąbelkowe](src/algorithms/sorting/bubble-sort)
  * `B` [Sortowanie przez wymiane](src/algorithms/sorting/selection-sort)
  * `B` [Sortowanie przez wstawianie](src/algorithms/sorting/insertion-sort)
  * `B` [Sortowanie stogowe](src/algorithms/sorting/heap-sort)
  * `B` [Sortowanie przez scalanie](src/algorithms/sorting/merge-sort)
  * `B` [Sortowanie szybkie](src/algorithms/sorting/quick-sort) - wdrożenia w miejscu i nie na miejscu
  * `B` [Sortowanie Shella](src/algorithms/sorting/shell-sort)
  * `B` [Sortowanie przez zliczanie](src/algorithms/sorting/counting-sort)
  * `B` [Sortowanie pozycyjne](src/algorithms/sorting/radix-sort)
* **Drzewa**
  * `B` [Przeszukiwanie w głąb](src/algorithms/tree/depth-first-search) (DFS)
  * `B` [Przeszukiwanie wszerz](src/algorithms/tree/breadth-first-search) (BFS)
* **Grafy**
  * `B` [Przeszukiwanie w głąb](src/algorithms/graph/depth-first-search) (DFS)
  * `B` [Przeszukiwanie wszerz](src/algorithms/graph/breadth-first-search) (BFS)
  * `B` [Algorytm Kruskala](src/algorithms/graph/kruskal) - znalezienie Minimalnego Drzewa Opinającego (MST) dla ważonego nieukierunkowanego wykresu
  * `A` [Algorytm Dijkstry](src/algorithms/graph/dijkstra) - znajdowanie  najkrótszej ścieżki z pojedynczego źródła w grafie
  * `A` [Algorytm Bellmana-Forda](src/algorithms/graph/bellman-ford) - znajdowanie najkrótszych ścieżek do wszystkich wierzchołków wykresu z jednego wierzchołka
  * `A` [Algorytm Floyd-Warshalla](src/algorithms/graph/floyd-warshall) - znajdź najkrótsze ścieżki między wszystkimi parami wierzchołków
  * `A` [Detect Cycle](src/algorithms/graph/detect-cycle) - zarówno dla wykresów skierowanych, jak i nieukierunkowanych(wersje oparte na DFS i Rozłączny Zestaw)
  * `A` [Algorytm Prima](src/algorithms/graph/prim) - znalezienie Minimalnego Drzewa Opinającego (MST) dla ważonego nieukierunkowanego wykresu
  * `A` [Sortowanie Topologiczne](src/algorithms/graph/topological-sorting) - metoda DFS 
  * `A` [Punkty Artykulacji](src/algorithms/graph/articulation-points) - Algorytm Tarjana (oparty o DFS)
  * `A` [Mosty](src/algorithms/graph/bridges) - Oparty na algorytmie DFS 
  * `A` [Ścieżka Euleriana i Obwód Euleriana](src/algorithms/graph/eulerian-path) - Algorytm Fleurya - Odwiedź każdą krawędź dokładnie raz
  * `A` [Cykl Hamiltoniana](src/algorithms/graph/hamiltonian-cycle) - Odwiedź każdy wierzchołek dokładnie raz
  * `A` [Silnie Połączone Komponenty](src/algorithms/graph/strongly-connected-components) - Algorytm Kosaraja 
  * `A` [Travelling Salesman Problem](src/algorithms/graph/travelling-salesman) - najkrótsza ścieżka która odwiedza każde miasto i wraca miasta początkującego
* **Niezkategorizowane**
  * `B` [Wieża Hanoi](src/algorithms/uncategorized/hanoi-tower)
  * `B` [Kwadratowa Matryca Obrotu](src/algorithms/uncategorized/square-matrix-rotation) - algorytm w miejscu
  * `B` [Jump Game](src/algorithms/uncategorized/jump-game) - cofanie, dynamiczne programowanie (od góry do dołu + od dołu do góry) i przykłady chciwego  
  * `B` [Unikatowe Ścieżki](src/algorithms/uncategorized/unique-paths) - cofanie, dynamiczne programowanie i przykłady oparte na Trójkącie Pascala
  * `A` [Problem N-Queens](src/algorithms/uncategorized/n-queens)
  * `A` [Knight's Tour](src/algorithms/uncategorized/knight-tour)

### Algorytmy według paradygmatu

Paradygmat algorytmiczny jest ogólną metodą lub podejściem, które jest 
podstawą projektowania klasy algorytmów. Jest abstrakcją wyższą niż 
pojęcie algorytmu, podobnie jak algorytm jest abstrakcją wyższą niż 
program komputerowy.

* **Metoda Siłowa** - Sprawdza wszystkie możliwosci i wybiera  najlepsze rozwiązanie.
  * `B` [Wyszukiwanie Liniowe](src/algorithms/search/linear-search)
  * `A` [Maksymalna Podtablica](src/algorithms/sets/maximum-subarray)
  * `A` [Problem z Podróżującym Sprzedawcą](src/algorithms/graph/travelling-salesman) - najkrótsza możliwa trasa, która odwiedza każde miasto i wraca do miasta początkowego
* **Chciwy** - wybierz najlepszą opcję w obecnym czasie, bez względu na przyszłość
  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
  * `A` [Niezwiązany Problem Knapsacka ](src/algorithms/sets/knapsack-problem)
  * `A` [Algorytm Dijkstry](src/algorithms/graph/dijkstra) - 
znalezienie najkrótszej ścieżki do wszystkich wierzchołków grafu
  * `A` [Algorytm Prima](src/algorithms/graph/prim) - znalezienie Minimalnego Drzewa Opinającego (MST) dla ważonego nieukierunkowanego wykresu
  * `A` [Algorytm Kruskala](src/algorithms/graph/kruskal) - znalezienie Minimalnego Drzewa Opinającego (MST) dla ważonego nieukierunkowanego wykresu
* **Dziel i Zwyciężaj** - podziel problem na mniejsze części, a następnie rozwiąż te części
  * `B` [Wyszukiwanie Binarne](src/algorithms/search/binary-search)
  * `B` [Wieża Hanoi](src/algorithms/uncategorized/hanoi-tower)
  * `B` [Trójkąt Pascala](src/algorithms/math/pascal-triangle)
  * `B` [Algorytm Euclideana](src/algorithms/math/euclidean-algorithm) - obliczyć Największy Wspólny Dzielnik(GCD)
  * `B` [Sortowanie przez scalanie](src/algorithms/sorting/merge-sort)
  * `B` [Szybkie Sortowanie](src/algorithms/sorting/quick-sort)
  * `B` [Drzewo Przeszukiwania W Głąb](src/algorithms/tree/depth-first-search) (DFS)
  * `B` [Graf Przeszukiwania W Głąb](src/algorithms/graph/depth-first-search) (DFS)
  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
  * `A` [Permutacje](src/algorithms/sets/permutations) (z albo bez powtórzeń)
  * `A` [Kombinacje](src/algorithms/sets/combinations) (z albo bez powtórzeń)
* **Programowanie Dynamiczne** - zbuduj rozwiązanie, korzystając z wcześniej znalezionych podrzędnych rozwiązań
  * `B` [Ciąg Fibonacciego](src/algorithms/math/fibonacci)
  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
  * `B` [Unikatowe Scieżki](src/algorithms/uncategorized/unique-paths)
  * `A` [Dystans Levenshteina](src/algorithms/string/levenshtein-distance) - minimalna odległość edycji między dwiema sekwencjami
  * `A` [Najdłuższa Wspólna Podsekwencja](src/algorithms/sets/longest-common-subsequence) (LCS)
  * `A` [Najdłuższa Wspólna Podłańcucha](src/algorithms/string/longest-common-substring)
  * `A` [Najdłuższa Wzrostająca Podsekwencja](src/algorithms/sets/longest-increasing-subsequence)
  * `A` [Najkrótsza Wspólna Supersekwencja](src/algorithms/sets/shortest-common-supersequence)
  * `A` [0/1 Problem Knapsacka](src/algorithms/sets/knapsack-problem)
  * `A` [Partycja Całkowita](src/algorithms/math/integer-partition)
  * `A` [Maksymalne Podtablice](src/algorithms/sets/maximum-subarray)
  * `A` [Algorytm Bellman-Forda](src/algorithms/graph/bellman-ford) - znalezienie najkrótszej ścieżki wszystkich wierzchołków wykresu
  * `A` [Algorytm Floyd-Warshalla](src/algorithms/graph/floyd-warshall) - 
znajdź najkrótsze ścieżki między wszystkimi parami wierzchołków
  * `A` [Dopasowanie Wyrażeń Regularnych](src/algorithms/string/regular-expression-matching)
* **Algorytm z nawrotami** - podobny do metody siłowej, próbuje wygenerować wszystkie możliwe rozwiązania, jednak za każdym razem generujesz następne rozwiązanie które testujesz
jeżeli zaspokaja wszystkie warunki, tylko wtedy generuje kolejne rozwiązania. W innym wypadku, cofa sie, i podąża inna ścieżka znaleźenia rozwiązania. Zazwyczaj, używane jest przejście przez Przeszukiwania W Głąb(DFS) przestrzeni stanów.
  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
  * `B` [Unikatowe Scieżki](src/algorithms/uncategorized/unique-paths)
  * `A` [Cykl Hamiltoniana](src/algorithms/graph/hamiltonian-cycle) - Odwiedź każdy wierzchołek dokładnie raz
  * `A` [Problem N-Queens](src/algorithms/uncategorized/n-queens)
  * `A` [Knight's Tour](src/algorithms/uncategorized/knight-tour)
  * `A` [Zestaw Sumy](src/algorithms/sets/combination-sum) - znajduje wszystkie zestawy które tworzą określoną sumę
* **Metoda Podziału i Ograniczeń** - Pamięta o niskonakładowym rozwiązaniu znalezionym na każdym etapie szukania nawrotu,
używa kosztu niskonakładowego kosztu, które dotychczas zostało znalezione jako niska granica najmniejszego kosztu
do rozwiązanie problemu, aby odrzucić cząstkowe rozwiązania o kosztach większych niż niskonakładowe
rozwiązanie znalezione do tej pory. 
Zazwyczan trajektoria BFS, w połączeniu z trajektorią Przeszukiwania W Głąb (DFS) drzewa przestrzeni stanów jest użyte.

## Jak używać repozytorium

**Zainstaluj wszystkie zależnosci**
```
npm install
```

**Uruchom ESLint**

Możesz to uruchomić aby sprawdzić jakość kodu.

```
npm run lint
```

**Uruchom wszystkie testy**
```
npm test
```

**Uruchom testy używając określonej nazwy**
```
npm test -- 'LinkedList'
```

**Playground**

Możesz pociwiczyć ze strukturą danych i algorytmami w `./src/playground/playground.js` zakartotekuj i napisz
testy do tego w `./src/playground/__test__/playground.test.js`.

Następnie uruchom następującą komendę w celu przetestowania czy twoje kod działa według oczekiwań: 

```
npm test -- 'playground'
```

## Pomocne informacje

### Źródła

[â–¶ Struktury Danych i Algorytmy na YouTube](https://www.youtube.com/playlist?list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)

### Big O Notacja

Kolejność wzrastania algorytmów według Big O notacji. 

![Big O grafy](./assets/big-o-graph.png)

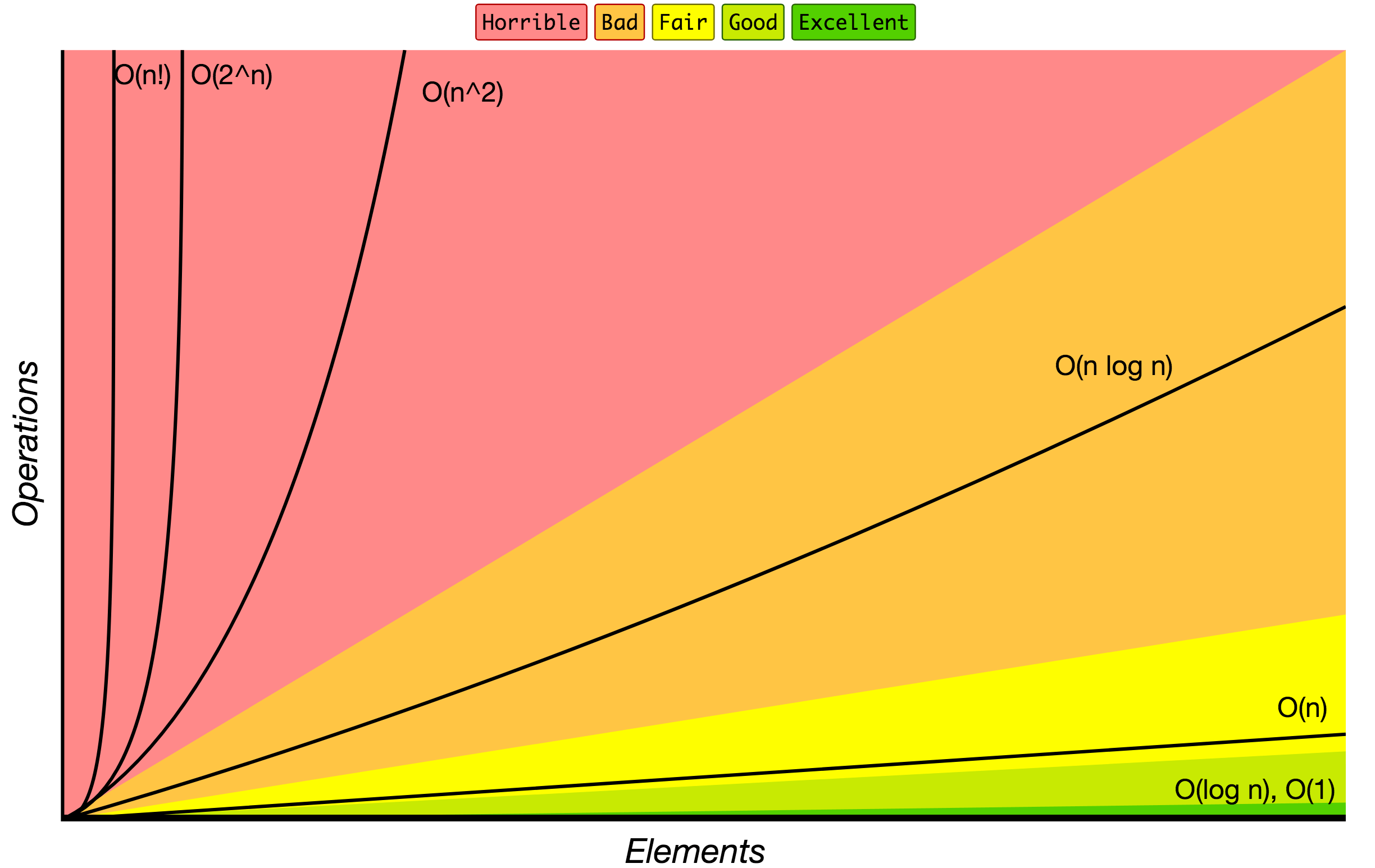
Źródło: [Big O Cheat Sheet](http://bigocheatsheet.com/).

Poniżej umieszczamy listę najbardziej używanych Big O notacji i ich porównania wydajności do róznych rozmiarów z wprowadzonych danych.

| Big O notacja  | Obliczenia na 10 elementów   | Obliczenia na 100 elementów   | Obliczenia na 1000 elementów    |
| -------------- | ---------------------------- | ----------------------------- | ------------------------------- |
| **O(1)**       | 1                            | 1                             | 1                               |
| **O(log N)**   | 3                            | 6                             | 9                               |
| **O(N)**       | 10                           | 100                           | 1000                            |
| **O(N log N)** | 30                           | 600                           | 9000                            |
| **O(N^2)**     | 100                          | 10000                         | 1000000                         |
| **O(2^N)**     | 1024                         | 1.26e+29                      | 1.07e+301                       |
| **O(N!)**      | 3628800                      | 9.3e+157                      | 4.02e+2567                      |

### Złożoność operacji struktury danych

| Struktura Danych                | Dostęp    | Szukaj    | Umieszczanie | Usuwanie  | Komentarze   |
| ------------------------------- | :-------: | :-------: | :----------: | :-------: | :----------- |
| **Szereg**                      | 1         | n         | n            | n         |              |
| **Sterta**                      | n         | n         | 1            | 1         |              |
| **Kolejka**                     | n         | n         | 1            | 1         |              |
| **Lista Powiązana**             | n         | n         | 1            | 1         |              |
| **Tablica funkcji mieszanej**   | -         | n         | n            | n         | W wypadku idealnej funkcji skrótu koszt mógłby sie równać O(1) |
| **Binarne Drzewo Poszukiwań**   | n         | n         | n            | n         | W przypadku zrównoważonych kosztów drzew byłoby O(log(n)) |
| **B-Drzewo**                    | log(n)    | log(n)    | log(n)       | log(n)    |              |
| **Drzewa czerwono-czarne**      | log(n)    | log(n)    | log(n)       | log(n)    |              |
| **AVL Drzewo**                  | log(n)    | log(n)    | log(n)       | log(n)    |              |
| **Filtr Blooma**                | -         | 1         | 1            | -         | Fałszywe dotatnie są możliwe podczas wyszukiwania |

### Sortowanie Tablic Złożoności Algorytmów

| Nazwa                               | Najlepszy       | Średni              | Najgorszy           | Pamięć    | Stabilność  | Komentarze  |
| ----------------------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :---------: | :---------- |
| **Sortowanie bąbelkowe**            | n               | n<sup>2</sup>       | n<sup>2</sup>       | 1         | Yes         |             |
| **Sortowanie przez wstawianie**     | n               | n<sup>2</sup>       | n<sup>2</sup>       | 1         | Yes         |             |
| **Sortowanie przez wybieranie**     | n<sup>2</sup>   | n<sup>2</sup>       | n<sup>2</sup>       | 1         | No          |             |
| **Sortowanie przez kopcowanie**     | n&nbsp;log(n)   | n&nbsp;log(n)       | n&nbsp;log(n)       | 1         | No          |             |
| **Sortowanie przez scalanie**       | n&nbsp;log(n)   | n&nbsp;log(n)       | n&nbsp;log(n)       | n         | Yes         |             |
| **Szybkie sortowanie**              | n&nbsp;log(n)   | n&nbsp;log(n)       | n<sup>2</sup>       | log(n)    | No          | Szybkie sortowanie jest zazwyczaj robione w miejsce O(log(n)) stosu przestrzeni |
| **Sortowanie Shella**               | n&nbsp;log(n)   | zależy od luki w układzie   | n&nbsp;(log(n))<sup>2</sup>  | 1         | No         |           |
| **Sortowanie przez zliczanie**      | n + r           | n + r               | n + r               | n + r     | Yes         | r - największy numer w tablicy|
| **Sortowanie Radix**                | n * k           | n * k               | n * k               | n + k     | Yes         | k -długość najdłuższego klucza |