# Estrutura de Dados e Algoritmos em JavaScript

[![CI](https://github.com/trekhleb/javascript-algorithms/workflows/CI/badge.svg)](https://github.com/trekhleb/javascript-algorithms/actions?query=workflow%3ACI+branch%3Amaster)
[![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)

Este repositório contém exemplos baseados em JavaScript de muitos
algoritmos e estruturas de dados populares.

Cada algoritmo e estrutura de dado possui seu próprio README
com explicações relacionadas e links para leitura adicional (incluindo
vídeos para YouTube)

_Leia isto em outros idiomas:_
[_English_](https://github.com/trekhleb/javascript-algorithms/)
[_简体中文_](README.zh-CN.md),
[_繁體中文_](README.zh-TW.md),
[_한국어_](README.ko-KR.md),
[_日本語_](README.ja-JP.md),
[_Polski_](README.pl-PL.md),
[_Français_](README.fr-FR.md),
[_Español_](README.es-ES.md),
[_Русский_](README.ru-RU.md),
[_Türk_](README.tr-TR.md),
[_Italiana_](README.it-IT.md)

## Estrutura de Dados

Uma estrutura de dados é uma maneira particular de organizar e armazenar dados em um computador para que ele possa
ser acessado e modificado de forma eficiente. Mais precisamente, uma estrutura de dados é uma coleção de dados
valores, as relações entre eles e as funções ou operações que podem ser aplicadas a
os dados.

`B` - Iniciante, `A` - Avançado

* `B` [Lista Encadeada (Linked List)](src/data-structures/linked-list/README.pt-BR.md)
* `B` [Lista Duplamente Ligada (Doubly Linked List)](src/data-structures/doubly-linked-list/README.pt-BR.md)
* `B` [Fila (Queue)](src/data-structures/queue/README.pt-BR.md)
* `B` [Stack](src/data-structures/stack/README.pt-BR.md)
* `B` [Tabela de Hash (Hash Table)](src/data-structures/hash-table/README.pt-BR.md)
* `B` [Heap](src/data-structures/heap/README.pt-BR.md)
* `B` [Fila de Prioridade (Priority Queue)](src/data-structures/priority-queue/README.pt-BR.md)
* `A` [Árvore de prefixos (Trie)](src/data-structures/trie/README.pt-BR.md)
* `A` [Árvore (Tree)](src/data-structures/tree/README.pt-BR.md)
  * `A` [Árvore de Pesquisa Binária (Binary Search Tree)](src/data-structures/tree/binary-search-tree/README.pt-BR.md)
  * `A` [Árvore AVL (AVL Tree)](src/data-structures/tree/avl-tree/README.pt-BR.md)
  * `A` [Árvore Vermelha-Preta (Red-Black Tree)](src/data-structures/tree/red-black-tree/README.pt-BR.md)
  * `A` [Árvore de Segmento (Segment Tree)](src/data-structures/tree/segment-tree/README.pt-BR.md) - com exemplos de consultas min / max / sum range
  * `A` [Árvore Fenwick (Fenwick Tree)](src/data-structures/tree/fenwick-tree/README.pt-BR.md) (Árvore indexada binária)
* `A` [Gráfico (Graph)](src/data-structures/graph/README.pt-BR.md) (ambos dirigidos e não direcionados)
* `A` [Conjunto Disjuntor (Disjoint Set)](src/data-structures/disjoint-set/README.pt-BR.md)
* `A` [Filtro Bloom (Bloom Filter)](src/data-structures/bloom-filter/README.pt-BR.md)

## Algoritmos

Um algoritmo é uma especificação inequívoca de como resolver uma classe de problemas. Isto é
um conjunto de regras que define precisamente uma sequência de operações.

`B` - Iniciante, `A` - Avançado

### Algoritmos por Tópico

* **Matemática**
  * `B` [Manipulação Bit](src/algorithms/math/bits) - set/get/update/clear bits, multiplicação / divisão por dois, tornar negativo etc.
  * `B` [Fatorial](src/algorithms/math/factorial)
  * `B` [Número de Fibonacci](src/algorithms/math/fibonacci)
  * `B` [Teste de Primalidade](src/algorithms/math/primality-test) (método de divisão experimental)
  * `B` [Algoritmo Euclidiano](src/algorithms/math/euclidean-algorithm) - calcular o maior divisor comum (GCD)
  * `B` [Mínimo múltiplo comum](src/algorithms/math/least-common-multiple) (LCM)
  * `B` [Peneira de Eratóstenes](src/algorithms/math/sieve-of-eratosthenes) - encontrar todos os números primos até um determinado limite
  * `B` [Potência de dois](src/algorithms/math/is-power-of-two) - verifique se o número é a potência de dois (algoritmos ingênuos e bit a bit)
  * `B` [Triângulo de Pascal](src/algorithms/math/pascal-triangle)
  * `B` [Número complexo](src/algorithms/math/complex-number) - números complexos e operações básicas com eles
  * `A` [Partição inteira](src/algorithms/math/integer-partition)
  * `A` [Algoritmo Liu Hui π](src/algorithms/math/liu-hui) - cálculos aproximados de π baseados em N-gons
* **Conjuntos**
  * `B` [Produto cartesiano](src/algorithms/sets/cartesian-product) - produto de vários conjuntos
  * `B` [Permutações de Fisher–Yates](src/algorithms/sets/fisher-yates) - permutação aleatória de uma sequência finita
  * `A` [Potência e Conjunto](src/algorithms/sets/power-set) - todos os subconjuntos de um conjunto
  * `A` [Permutações](src/algorithms/sets/permutations) (com e sem repetições)
  * `A` [Combinações](src/algorithms/sets/combinations) (com e sem repetições)
  * `A` [Mais longa subsequência comum](src/algorithms/sets/longest-common-subsequence) (LCS)
  * `A` [Maior subsequência crescente](src/algorithms/sets/longest-increasing-subsequence)
  * `A` [Supersequência Comum mais curta](src/algorithms/sets/shortest-common-supersequence) (SCS)
  * `A` [Problema da mochila](src/algorithms/sets/knapsack-problem) - "0/1" e "Não consolidado"
  * `A` [Máximo Subarray](src/algorithms/sets/maximum-subarray) - "Força bruta" e " Programação Dinâmica" versões (Kadane's)
  * `A` [Soma de Combinação](src/algorithms/sets/combination-sum) - encontre todas as combinações que formam uma soma específica
* **Cadeia de Caracteres**
  * `B` [Hamming Distance](src/algorithms/string/hamming-distance) - número de posições em que os símbolos são diferentes
  * `A` [Levenshtein Distance](src/algorithms/string/levenshtein-distance) - distância mínima de edição entre duas sequências
  * `A` [Knuth–Morris–Pratt Algorithm](src/algorithms/string/knuth-morris-pratt) (Algoritmo KMP) - pesquisa de substring (correspondência de padrão)
  * `A` [Z Algorithm](src/algorithms/string/z-algorithm) - pesquisa de substring (correspondência de padrão)
  * `A` [Rabin Karp Algorithm](src/algorithms/string/rabin-karp) - pesquisa de substring
  * `A` [Longest Common Substring](src/algorithms/string/longest-common-substring)
  * `A` [Regular Expression Matching](src/algorithms/string/regular-expression-matching)
* **Buscas**
  * `B` [Linear Search](src/algorithms/search/linear-search)
  * `B` [Jump Search](src/algorithms/search/jump-search) (ou Bloquear pesquisa) - pesquisar na matriz ordenada
  * `B` [Binary Search](src/algorithms/search/binary-search) - pesquisar na matriz ordenada
  * `B` [Interpolation Search](src/algorithms/search/interpolation-search) - pesquisar em matriz classificada uniformemente distribuída
* **Classificação**
  * `B` [Bubble Sort](src/algorithms/sorting/bubble-sort)
  * `B` [Selection Sort](src/algorithms/sorting/selection-sort)
  * `B` [Insertion Sort](src/algorithms/sorting/insertion-sort)
  * `B` [Heap Sort](src/algorithms/sorting/heap-sort)
  * `B` [Merge Sort](src/algorithms/sorting/merge-sort)
  * `B` [Quicksort](src/algorithms/sorting/quick-sort) - implementações local e não local
  * `B` [Shellsort](src/algorithms/sorting/shell-sort)
  * `B` [Counting Sort](src/algorithms/sorting/counting-sort)
  * `B` [Radix Sort](src/algorithms/sorting/radix-sort)
* **Arvóres**
  * `B` [Depth-First Search](src/algorithms/tree/depth-first-search) (DFS)
  * `B` [Breadth-First Search](src/algorithms/tree/breadth-first-search) (BFS)
* **Gráficos**
  * `B` [Depth-First Search](src/algorithms/graph/depth-first-search) (DFS)
  * `B` [Breadth-First Search](src/algorithms/graph/breadth-first-search) (BFS)
  * `B` [Kruskal’s Algorithm](src/algorithms/graph/kruskal) - encontrando Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
  * `A` [Dijkstra Algorithm](src/algorithms/graph/dijkstra) - encontrar caminhos mais curtos para todos os vértices do grafo a partir de um único vértice
  * `A` [Bellman-Ford Algorithm](src/algorithms/graph/bellman-ford) - encontrar caminhos mais curtos para todos os vértices do grafo a partir de um único vértice
  * `A` [Floyd-Warshall Algorithm](src/algorithms/graph/floyd-warshall) - encontrar caminhos mais curtos entre todos os pares de vértices
  * `A` [Detect Cycle](src/algorithms/graph/detect-cycle) - para gráficos direcionados e não direcionados (versões baseadas em DFS e Conjunto Disjuntivo)
  * `A` [Prim’s Algorithm](src/algorithms/graph/prim) - encontrando Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
  * `A` [Topological Sorting](src/algorithms/graph/topological-sorting) - Métodos DFS
  * `A` [Articulation Points](src/algorithms/graph/articulation-points) -O algoritmo de Tarjan (baseado em DFS)
  * `A` [Bridges](src/algorithms/graph/bridges) - Algoritmo baseado em DFS
  * `A` [Eulerian Path and Eulerian Circuit](src/algorithms/graph/eulerian-path) - Algoritmo de Fleury - Visite todas as bordas exatamente uma vez
  * `A` [Hamiltonian Cycle](src/algorithms/graph/hamiltonian-cycle) - Visite todas as bordas exatamente uma vez
  * `A` [Strongly Connected Components](src/algorithms/graph/strongly-connected-components) - Algoritmo de Kosaraju's
  * `A` [Travelling Salesman Problem](src/algorithms/graph/travelling-salesman) - rota mais curta possível que visita cada cidade e retorna à cidade de origem
* **criptografia**
  * `B` [Polynomial Hash](src/algorithms/cryptography/polynomial-hash) - função de hash de rolagem baseada em polinômio
* **Sem categoria**
  * `B` [Tower of Hanoi](src/algorithms/uncategorized/hanoi-tower)
  * `B` [Square Matrix Rotation](src/algorithms/uncategorized/square-matrix-rotation) - algoritmo no local
  * `B` [Jump Game](src/algorithms/uncategorized/jump-game) - backtracking, programação dinâmica (top-down + bottom-up) e exemplos gananciosos
  * `B` [Unique Paths](src/algorithms/uncategorized/unique-paths) - backtracking, programação dinâmica e exemplos baseados no triângulo de Pascal
  * `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - trapping problema da água da chuva (programação dinâmica e versões de força bruta)
  * `A` [N-Queens Problem](src/algorithms/uncategorized/n-queens)
  * `A` [Knight's Tour](src/algorithms/uncategorized/knight-tour)

### Algoritmos por Paradigma

Um paradigma algorítmico é um método ou abordagem genérica subjacente ao design de uma classe
de algoritmos. É uma abstração maior do que a noção de um algoritmo, assim como
algoritmo é uma abstração maior que um programa de computador.

* **Força bruta** - look at all the possibilities and selects the best solution
  * `B` [Linear Search](src/algorithms/search/linear-search)
  * `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - trapping problema da água da chuva
  * `A` [Maximum Subarray](src/algorithms/sets/maximum-subarray)
  * `A` [Travelling Salesman Problem](src/algorithms/graph/travelling-salesman) - rota mais curta possível que visita cada cidade e retorna à cidade de origem
* **Greedy** - choose the best option at the current time, without any consideration for the future
  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
  * `A` [Unbound Knapsack Problem](src/algorithms/sets/knapsack-problem)
  * `A` [Dijkstra Algorithm](src/algorithms/graph/dijkstra) - finding shortest path to all graph vertices
  * `A` [Prim’s Algorithm](src/algorithms/graph/prim) - encontrando Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
  * `A` [Kruskal’s Algorithm](src/algorithms/graph/kruskal) - encontrando Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
* **Divide and Conquer** - dividir o problema em partes menores e depois resolver essas partes
  * `B` [Binary Search](src/algorithms/search/binary-search)
  * `B` [Tower of Hanoi](src/algorithms/uncategorized/hanoi-tower)
  * `B` [Pascal's Triangle](src/algorithms/math/pascal-triangle)
  * `B` [Euclidean Algorithm](src/algorithms/math/euclidean-algorithm) - calculate the Greatest Common Divisor (GCD)
  * `B` [Merge Sort](src/algorithms/sorting/merge-sort)
  * `B` [Quicksort](src/algorithms/sorting/quick-sort)
  * `B` [Tree Depth-First Search](src/algorithms/tree/depth-first-search) (DFS)
  * `B` [Graph Depth-First Search](src/algorithms/graph/depth-first-search) (DFS)
  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
  * `A` [Permutations](src/algorithms/sets/permutations) (com e sem repetições)
  * `A` [Combinations](src/algorithms/sets/combinations) (com e sem repetições)
* **Dynamic Programming** - criar uma solução usando sub-soluções encontradas anteriormente
  * `B` [Fibonacci Number](src/algorithms/math/fibonacci)
  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
  * `B` [Unique Paths](src/algorithms/uncategorized/unique-paths)
  * `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - trapping problema da água da chuva
  * `A` [Levenshtein Distance](src/algorithms/string/levenshtein-distance) - distância mínima de edição entre duas sequências
  * `A` [Longest Common Subsequence](src/algorithms/sets/longest-common-subsequence) (LCS)
  * `A` [Longest Common Substring](src/algorithms/string/longest-common-substring)
  * `A` [Longest Increasing Subsequence](src/algorithms/sets/longest-increasing-subsequence)
  * `A` [Shortest Common Supersequence](src/algorithms/sets/shortest-common-supersequence)
  * `A` [0/1 Knapsack Problem](src/algorithms/sets/knapsack-problem)
  * `A` [Integer Partition](src/algorithms/math/integer-partition)
  * `A` [Maximum Subarray](src/algorithms/sets/maximum-subarray)
  * `A` [Bellman-Ford Algorithm](src/algorithms/graph/bellman-ford) - encontrando o caminho mais curto para todos os vértices do gráfico
  * `A` [Floyd-Warshall Algorithm](src/algorithms/graph/floyd-warshall) - encontrar caminhos mais curtos entre todos os pares de vértices
  * `A` [Regular Expression Matching](src/algorithms/string/regular-expression-matching)
* **Backtracking** - da mesma forma que a força bruta, tente gerar todas as soluções possíveis, mas cada vez que você gerar a próxima solução, você testará
se satisfizer todas as condições, e só então continuar gerando soluções subseqüentes. Caso contrário, volte atrás e siga um caminho diferente para encontrar uma solução. Normalmente, a passagem DFS do espaço de estados está sendo usada.
  * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
  * `B` [Unique Paths](src/algorithms/uncategorized/unique-paths)
  * `A` [Hamiltonian Cycle](src/algorithms/graph/hamiltonian-cycle) - Visite todos os vértices exatamente uma vez
  * `A` [N-Queens Problem](src/algorithms/uncategorized/n-queens)
  * `A` [Knight's Tour](src/algorithms/uncategorized/knight-tour)
  * `A` [Combination Sum](src/algorithms/sets/combination-sum) - encontre todas as combinações que formam uma soma específica
* **Branch & Bound** - lembre-se da solução de menor custo encontrada em cada etapa do retrocesso
pesquisar e usar o custo da solução de menor custo encontrada até o limite inferior do custo de
solução de menor custo para o problema, a fim de descartar soluções parciais com custos maiores que o
solução de menor custo encontrada até o momento. Normalmente, a travessia BFS em combinação com a passagem DFS do espaço de estados
árvore está sendo usada

## Como usar este repositório

**Instalar todas as dependências**
```
npm install
```

**Executar o ESLint**

Você pode querer executá-lo para verificar a qualidade do código.

```
npm run lint
```

**Execute todos os testes**
```
npm test
```

**Executar testes por nome**
```
npm test -- 'LinkedList'
```

**Parque infantil**

Você pode brincar com estruturas de dados e algoritmos em `./src/playground/playground.js` arquivar e escrever
testes para isso em `./src/playground/__test__/playground.test.js`.

Em seguida, basta executar o seguinte comando para testar se o código do seu playground funciona conforme o esperado:

```
npm test -- 'playground'
```

## Informação útil

### Referências

[▶ Estruturas de dados e algoritmos no YouTube](https://www.youtube.com/playlist?list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)

### Notação Big O

Ordem de crescimento dos algoritmos especificados em notação Big O.

![Notação Big-O](./assets/big-o-graph.png)

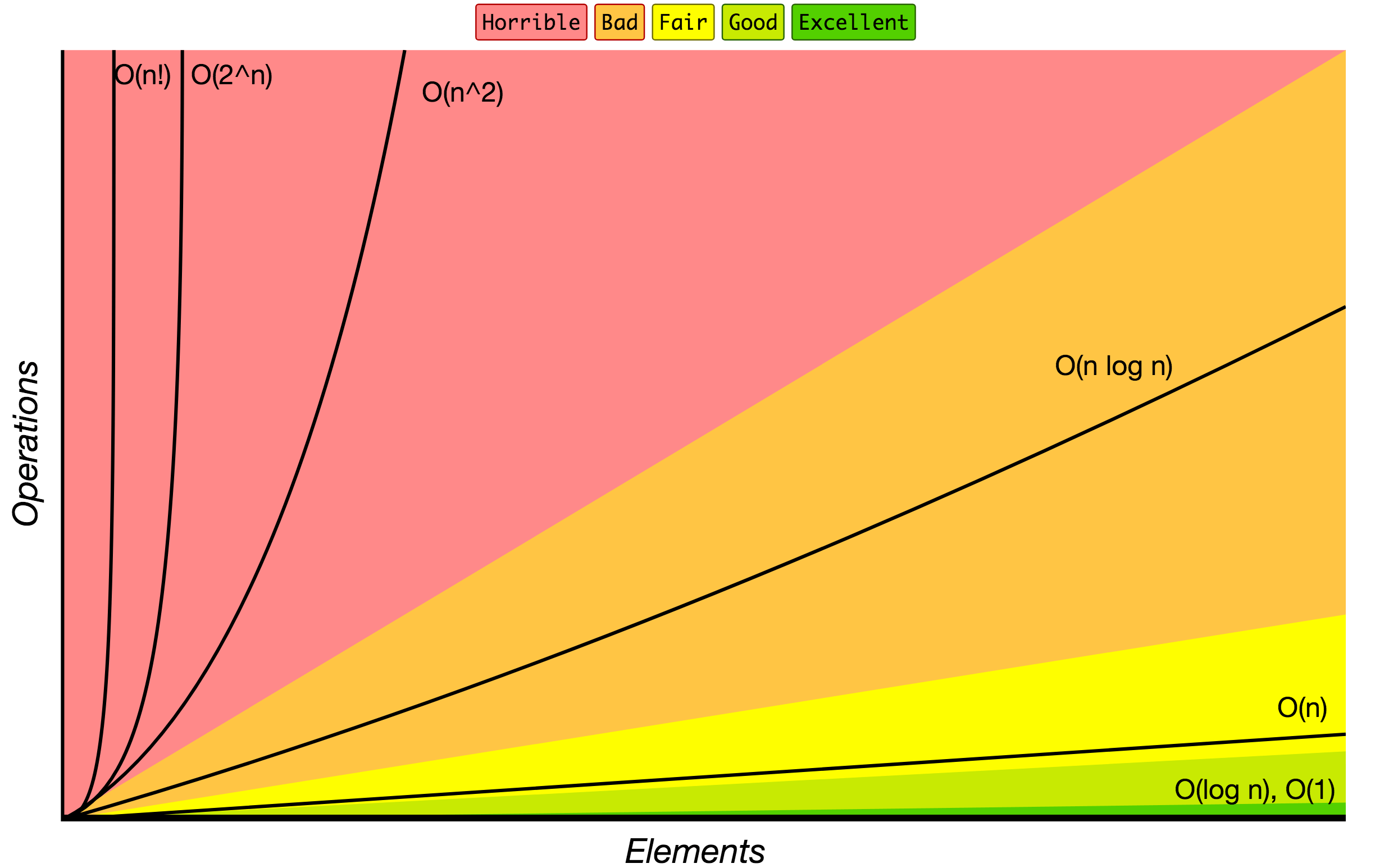
Fonte: [Notação Big-O dicas](http://bigocheatsheet.com/).

Abaixo está a lista de algumas das notações Big O mais usadas e suas comparações de desempenho em relação aos diferentes tamanhos dos dados de entrada.

| Notação Big-O  | Cálculos para 10 elementos   | Cálculos para 100 elementos   | Cálculos para 1000 elementos    |
| -------------- | ---------------------------- | ----------------------------- | ------------------------------- |
| **O(1)**       | 1                            | 1                             | 1                               |
| **O(log N)**   | 3                            | 6                             | 9                               |
| **O(N)**       | 10                           | 100                           | 1000                            |
| **O(N log N)** | 30                           | 600                           | 9000                            |
| **O(N^2)**     | 100                          | 10000                         | 1000000                         |
| **O(2^N)**     | 1024                         | 1.26e+29                      | 1.07e+301                       |
| **O(N!)**      | 3628800                      | 9.3e+157                      | 4.02e+2567                      |

### Complexidade de operações de estrutura de dados

| estrutura de dados      | Acesso    | Busca     | Inserção  | Eliminação | comentários |
| ----------------------- | :-------: | :-------: | :-------: | :-------:  | :--------   |
| **Array**               | 1         | n         | n         | n          |             |
| **Stack**               | n         | n         | 1         | 1          |             |
| **Queue**               | n         | n         | 1         | 1          |             |
| **Linked List**         | n         | n         | 1         | 1          |             |
| **Hash Table**          | -         | n         | n         | n          | Em caso de uma função hash perfeita, os custos seriam O (1) |
| **Binary Search Tree**  | n         | n         | n         | n          | No caso de custos de árvore equilibrados seria O (log (n))
| **B-Tree**              | log(n)    | log(n)    | log(n)    | log(n)     |             |
| **Red-Black Tree**      | log(n)    | log(n)    | log(n)    | log(n)     |             |
| **AVL Tree**            | log(n)    | log(n)    | log(n)    | log(n)     |             |
| **Bloom Filter**        | -         | 1         | 1         | -          | Falsos positivos são possíveis durante a pesquisa |

### Array Sorting Algorithms Complexity

| Nome                  | Melhor          | Média               | Pior                | Mémoria   | Estável   | comentários |
| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :--------   |
| **Bubble sort**       | n               | n<sup>2</sup>       | n<sup>2</sup>       | 1         | Sim       |             |
| **Insertion sort**    | n               | n<sup>2</sup>       | n<sup>2</sup>       | 1         | Sim       |             |
| **Selection sort**    | n<sup>2</sup>   | n<sup>2</sup>       | n<sup>2</sup>       | 1         | Não       |             |
| **Heap sort**         | n&nbsp;log(n)   | n&nbsp;log(n)       | n&nbsp;log(n)       | 1         | Não       |             |
| **Merge sort**        | n&nbsp;log(n)   | n&nbsp;log(n)       | n&nbsp;log(n)       | n         | Sim       |             |
| **Quick sort**        | n&nbsp;log(n)   | n&nbsp;log(n)       | n<sup>2</sup>       | log(n)    | Não       | O Quicksort geralmente é feito no local com o espaço de pilha O  O(log(n)) stack space |
| **Shell sort**        | n&nbsp;log(n)   | depende da sequência de lacunas | n&nbsp;(log(n))<sup>2</sup>     | 1      | Não    |                   |
| **Counting sort**     | n + r           | n + r               | n + r               | n + r     | Sim       | r - maior número na matriz          |
| **Radix sort**        | n * k           | n * k               | n * k               | n + k     | Sim       | k - comprimento da chave mais longa |