mirror of
https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git
synced 2024-11-10 11:09:43 +08:00
Merge branch 'master' into my-test
This commit is contained in:
commit
e076e12dee
@ -1,3 +1,4 @@
|
|||||||
|
# @see: https://editorconfig.org/
|
||||||
root = true
|
root = true
|
||||||
|
|
||||||
[*]
|
[*]
|
||||||
@ -6,3 +7,4 @@ insert_final_newline = true
|
|||||||
charset = utf-8
|
charset = utf-8
|
||||||
indent_style = space
|
indent_style = space
|
||||||
indent_size = 2
|
indent_size = 2
|
||||||
|
trim_trailing_whitespace = true
|
||||||
|
|||||||
@ -143,6 +143,7 @@ a set of rules that precisely define a sequence of operations.
|
|||||||
* `B` [Caesar Cipher](src/algorithms/cryptography/caesar-cipher) - simple substitution cipher
|
* `B` [Caesar Cipher](src/algorithms/cryptography/caesar-cipher) - simple substitution cipher
|
||||||
* **Machine Learning**
|
* **Machine Learning**
|
||||||
* `B` [NanoNeuron](https://github.com/trekhleb/nano-neuron) - 7 simple JS functions that illustrate how machines can actually learn (forward/backward propagation)
|
* `B` [NanoNeuron](https://github.com/trekhleb/nano-neuron) - 7 simple JS functions that illustrate how machines can actually learn (forward/backward propagation)
|
||||||
|
* `B` [k-NN](src/algorithms/ml/knn) - k-nearest neighbors classification algorithm
|
||||||
* **Uncategorized**
|
* **Uncategorized**
|
||||||
* `B` [Tower of Hanoi](src/algorithms/uncategorized/hanoi-tower)
|
* `B` [Tower of Hanoi](src/algorithms/uncategorized/hanoi-tower)
|
||||||
* `B` [Square Matrix Rotation](src/algorithms/uncategorized/square-matrix-rotation) - in-place algorithm
|
* `B` [Square Matrix Rotation](src/algorithms/uncategorized/square-matrix-rotation) - in-place algorithm
|
||||||
|
|||||||
@ -25,4 +25,14 @@ module.exports = {
|
|||||||
// It is reflected in properties such as location.href.
|
// It is reflected in properties such as location.href.
|
||||||
// @see: https://github.com/facebook/jest/issues/6769
|
// @see: https://github.com/facebook/jest/issues/6769
|
||||||
testURL: 'http://localhost/',
|
testURL: 'http://localhost/',
|
||||||
|
|
||||||
|
// @see: https://jestjs.io/docs/en/configuration#coveragethreshold-object
|
||||||
|
coverageThreshold: {
|
||||||
|
global: {
|
||||||
|
statements: 100,
|
||||||
|
branches: 95,
|
||||||
|
functions: 100,
|
||||||
|
lines: 100,
|
||||||
|
},
|
||||||
|
},
|
||||||
};
|
};
|
||||||
|
|||||||
41
src/algorithms/ml/knn/README.md
Normal file
41
src/algorithms/ml/knn/README.md
Normal file
@ -0,0 +1,41 @@
|
|||||||
|
# k-Nearest Neighbors Algorithm
|
||||||
|
|
||||||
|
The **k-nearest neighbors algorithm (k-NN)** is a supervised Machine Learning algorithm. It's a classification algorithm, determining the class of a sample vector using a sample data.
|
||||||
|
|
||||||
|
In k-NN classification, the output is a class membership. An object is classified by a plurality vote of its neighbors, with the object being assigned to the class most common among its `k` nearest neighbors (`k` is a positive integer, typically small). If `k = 1`, then the object is simply assigned to the class of that single nearest neighbor.
|
||||||
|
|
||||||
|
The idea is to calculate the similarity between two data points on the basis of a distance metric. [Euclidean distance](https://en.wikipedia.org/wiki/Euclidean_distance) is used mostly for this task.
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
_Image source: [Wikipedia](https://en.wikipedia.org/wiki/Euclidean_distance)_
|
||||||
|
|
||||||
|
The algorithm is as follows:
|
||||||
|
|
||||||
|
1. Check for errors like invalid data/labels.
|
||||||
|
2. Calculate the euclidean distance of all the data points in training data with the classification point
|
||||||
|
3. Sort the distances of points along with their classes in ascending order
|
||||||
|
4. Take the initial `K` classes and find the mode to get the most similar class
|
||||||
|
5. Report the most similar class
|
||||||
|
|
||||||
|
Here is a visualization of k-NN classification for better understanding:
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
_Image source: [Wikipedia](https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm)_
|
||||||
|
|
||||||
|
The test sample (green dot) should be classified either to blue squares or to red triangles. If `k = 3` (solid line circle) it is assigned to the red triangles because there are `2` triangles and only `1` square inside the inner circle. If `k = 5` (dashed line circle) it is assigned to the blue squares (`3` squares vs. `2` triangles inside the outer circle).
|
||||||
|
|
||||||
|
Another k-NN classification example:
|
||||||
|
|
||||||
|
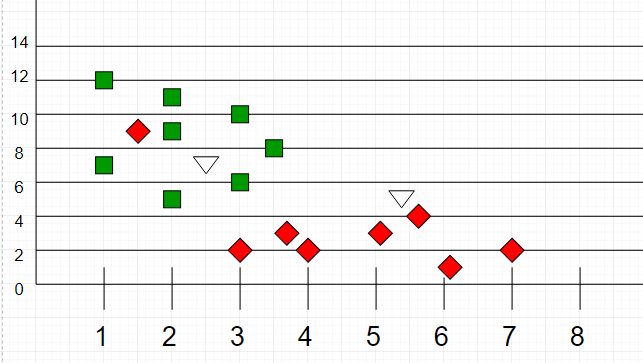
|
||||||
|
|
||||||
|
_Image source: [GeeksForGeeks](https://media.geeksforgeeks.org/wp-content/uploads/graph2-2.png)_
|
||||||
|
|
||||||
|
Here, as we can see, the classification of unknown points will be judged by their proximity to other points.
|
||||||
|
|
||||||
|
It is important to note that `K` is preferred to have odd values in order to break ties. Usually `K` is taken as `3` or `5`.
|
||||||
|
|
||||||
|
## References
|
||||||
|
|
||||||
|
- [k-nearest neighbors algorithm on Wikipedia](https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm)
|
||||||
71
src/algorithms/ml/knn/__test__/knn.test.js
Normal file
71
src/algorithms/ml/knn/__test__/knn.test.js
Normal file
@ -0,0 +1,71 @@
|
|||||||
|
import kNN from '../kNN';
|
||||||
|
|
||||||
|
describe('kNN', () => {
|
||||||
|
it('should throw an error on invalid data', () => {
|
||||||
|
expect(() => {
|
||||||
|
kNN();
|
||||||
|
}).toThrowError('Either dataSet or labels or toClassify were not set');
|
||||||
|
});
|
||||||
|
|
||||||
|
it('should throw an error on invalid labels', () => {
|
||||||
|
const noLabels = () => {
|
||||||
|
kNN([[1, 1]]);
|
||||||
|
};
|
||||||
|
expect(noLabels).toThrowError('Either dataSet or labels or toClassify were not set');
|
||||||
|
});
|
||||||
|
|
||||||
|
it('should throw an error on not giving classification vector', () => {
|
||||||
|
const noClassification = () => {
|
||||||
|
kNN([[1, 1]], [1]);
|
||||||
|
};
|
||||||
|
expect(noClassification).toThrowError('Either dataSet or labels or toClassify were not set');
|
||||||
|
});
|
||||||
|
|
||||||
|
it('should throw an error on not giving classification vector', () => {
|
||||||
|
const inconsistent = () => {
|
||||||
|
kNN([[1, 1]], [1], [1]);
|
||||||
|
};
|
||||||
|
expect(inconsistent).toThrowError('Inconsistent vector lengths');
|
||||||
|
});
|
||||||
|
|
||||||
|
it('should find the nearest neighbour', () => {
|
||||||
|
let dataSet;
|
||||||
|
let labels;
|
||||||
|
let toClassify;
|
||||||
|
let expectedClass;
|
||||||
|
|
||||||
|
dataSet = [[1, 1], [2, 2]];
|
||||||
|
labels = [1, 2];
|
||||||
|
toClassify = [1, 1];
|
||||||
|
expectedClass = 1;
|
||||||
|
expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass);
|
||||||
|
|
||||||
|
dataSet = [[1, 1], [6, 2], [3, 3], [4, 5], [9, 2], [2, 4], [8, 7]];
|
||||||
|
labels = [1, 2, 1, 2, 1, 2, 1];
|
||||||
|
toClassify = [1.25, 1.25];
|
||||||
|
expectedClass = 1;
|
||||||
|
expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass);
|
||||||
|
|
||||||
|
dataSet = [[1, 1], [6, 2], [3, 3], [4, 5], [9, 2], [2, 4], [8, 7]];
|
||||||
|
labels = [1, 2, 1, 2, 1, 2, 1];
|
||||||
|
toClassify = [1.25, 1.25];
|
||||||
|
expectedClass = 2;
|
||||||
|
expect(kNN(dataSet, labels, toClassify, 5)).toBe(expectedClass);
|
||||||
|
});
|
||||||
|
|
||||||
|
it('should find the nearest neighbour with equal distances', () => {
|
||||||
|
const dataSet = [[0, 0], [1, 1], [0, 2]];
|
||||||
|
const labels = [1, 3, 3];
|
||||||
|
const toClassify = [0, 1];
|
||||||
|
const expectedClass = 3;
|
||||||
|
expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass);
|
||||||
|
});
|
||||||
|
|
||||||
|
it('should find the nearest neighbour in 3D space', () => {
|
||||||
|
const dataSet = [[0, 0, 0], [0, 1, 1], [0, 0, 2]];
|
||||||
|
const labels = [1, 3, 3];
|
||||||
|
const toClassify = [0, 0, 1];
|
||||||
|
const expectedClass = 3;
|
||||||
|
expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass);
|
||||||
|
});
|
||||||
|
});
|
||||||
77
src/algorithms/ml/knn/kNN.js
Normal file
77
src/algorithms/ml/knn/kNN.js
Normal file
@ -0,0 +1,77 @@
|
|||||||
|
/**
|
||||||
|
* Calculates calculate the euclidean distance between 2 vectors.
|
||||||
|
*
|
||||||
|
* @param {number[]} x1
|
||||||
|
* @param {number[]} x2
|
||||||
|
* @returns {number}
|
||||||
|
*/
|
||||||
|
function euclideanDistance(x1, x2) {
|
||||||
|
// Checking for errors.
|
||||||
|
if (x1.length !== x2.length) {
|
||||||
|
throw new Error('Inconsistent vector lengths');
|
||||||
|
}
|
||||||
|
// Calculate the euclidean distance between 2 vectors and return.
|
||||||
|
let squaresTotal = 0;
|
||||||
|
for (let i = 0; i < x1.length; i += 1) {
|
||||||
|
squaresTotal += (x1[i] - x2[i]) ** 2;
|
||||||
|
}
|
||||||
|
return Number(Math.sqrt(squaresTotal).toFixed(2));
|
||||||
|
}
|
||||||
|
|
||||||
|
/**
|
||||||
|
* Classifies the point in space based on k-nearest neighbors algorithm.
|
||||||
|
*
|
||||||
|
* @param {number[][]} dataSet - array of data points, i.e. [[0, 1], [3, 4], [5, 7]]
|
||||||
|
* @param {number[]} labels - array of classes (labels), i.e. [1, 1, 2]
|
||||||
|
* @param {number[]} toClassify - the point in space that needs to be classified, i.e. [5, 4]
|
||||||
|
* @param {number} k - number of nearest neighbors which will be taken into account (preferably odd)
|
||||||
|
* @return {number} - the class of the point
|
||||||
|
*/
|
||||||
|
export default function kNN(
|
||||||
|
dataSet,
|
||||||
|
labels,
|
||||||
|
toClassify,
|
||||||
|
k = 3,
|
||||||
|
) {
|
||||||
|
if (!dataSet || !labels || !toClassify) {
|
||||||
|
throw new Error('Either dataSet or labels or toClassify were not set');
|
||||||
|
}
|
||||||
|
|
||||||
|
// Calculate distance from toClassify to each point for all dimensions in dataSet.
|
||||||
|
// Store distance and point's label into distances list.
|
||||||
|
const distances = [];
|
||||||
|
for (let i = 0; i < dataSet.length; i += 1) {
|
||||||
|
distances.push({
|
||||||
|
dist: euclideanDistance(dataSet[i], toClassify),
|
||||||
|
label: labels[i],
|
||||||
|
});
|
||||||
|
}
|
||||||
|
|
||||||
|
// Sort distances list (from closer point to further ones).
|
||||||
|
// Take initial k values, count with class index
|
||||||
|
const kNearest = distances.sort((a, b) => {
|
||||||
|
if (a.dist === b.dist) {
|
||||||
|
return 0;
|
||||||
|
}
|
||||||
|
return a.dist < b.dist ? -1 : 1;
|
||||||
|
}).slice(0, k);
|
||||||
|
|
||||||
|
// Count the number of instances of each class in top k members.
|
||||||
|
const labelsCounter = {};
|
||||||
|
let topClass = 0;
|
||||||
|
let topClassCount = 0;
|
||||||
|
for (let i = 0; i < kNearest.length; i += 1) {
|
||||||
|
if (kNearest[i].label in labelsCounter) {
|
||||||
|
labelsCounter[kNearest[i].label] += 1;
|
||||||
|
} else {
|
||||||
|
labelsCounter[kNearest[i].label] = 1;
|
||||||
|
}
|
||||||
|
if (labelsCounter[kNearest[i].label] > topClassCount) {
|
||||||
|
topClassCount = labelsCounter[kNearest[i].label];
|
||||||
|
topClass = kNearest[i].label;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
// Return the class with highest count.
|
||||||
|
return topClass;
|
||||||
|
}
|
||||||
@ -1,5 +1,8 @@
|
|||||||
# Bubble Sort
|
# Bubble Sort
|
||||||
|
|
||||||
|
_Read this in other languages:_
|
||||||
|
[_Português_](README.pt-BR.md)
|
||||||
|
|
||||||
Bubble sort, sometimes referred to as sinking sort, is a
|
Bubble sort, sometimes referred to as sinking sort, is a
|
||||||
simple sorting algorithm that repeatedly steps through
|
simple sorting algorithm that repeatedly steps through
|
||||||
the list to be sorted, compares each pair of adjacent
|
the list to be sorted, compares each pair of adjacent
|
||||||
|
|||||||
17
src/algorithms/sorting/bubble-sort/README.pt-BR.md
Normal file
17
src/algorithms/sorting/bubble-sort/README.pt-BR.md
Normal file
@ -0,0 +1,17 @@
|
|||||||
|
# Bubble Sort
|
||||||
|
|
||||||
|
O bubble sort, ou ordenação por flutuação (literalmente "por bolha"), é um algoritmo de ordenação dos mais simples. A ideia é percorrer o vetor diversas vezes, e a cada passagem fazer flutuar para o topo o maior elemento da sequência. Essa movimentação lembra a forma como as bolhas em um tanque de água procuram seu próprio nível, e disso vem o nome do algoritmo.
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
## Complexity
|
||||||
|
|
||||||
|
| Name | Best | Average | Worst | Memory | Stable | Comments |
|
||||||
|
| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
|
||||||
|
| **Bubble sort** | n | n<sup>2</sup> | n<sup>2</sup> | 1 | Yes | |
|
||||||
|
|
||||||
|
## References
|
||||||
|
|
||||||
|
- [Wikipedia](https://pt.wikipedia.org/wiki/Bubble_sort)
|
||||||
|
- [YouTube](https://www.youtube.com/watch?v=6Gv8vg0kcHc&index=27&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
|
||||||
|
|
||||||
@ -51,7 +51,7 @@ Remove(head, value)
|
|||||||
return true
|
return true
|
||||||
end if
|
end if
|
||||||
n ← head.next
|
n ← head.next
|
||||||
while n = ø and value = n.value
|
while n = ø and value !== n.value
|
||||||
n ← n.next
|
n ← n.next
|
||||||
end while
|
end while
|
||||||
if n = tail
|
if n = tail
|
||||||
|
|||||||
Loading…
Reference in New Issue
Block a user