Merge branch 'master' into my-test

.editorconfig

@@ -1,3 +1,4 @@
+# @see: https://editorconfig.org/
 root = true
 
 [*]
@@ -6,3 +7,4 @@ insert_final_newline = true
 charset = utf-8
 indent_style = space
 indent_size = 2
+trim_trailing_whitespace = true

README.es-ES.md

@@ -6,7 +6,7 @@
 Este repositorio contiene ejemplos basados en JavaScript de muchos
 algoritmos y estructuras de datos populares.
 
-Cada algoritmo y estructura de datos tiene su propio LÉAME con explicaciones relacionadas y 
+Cada algoritmo y estructura de datos tiene su propio LÉAME con explicaciones relacionadas y
 enlaces para lecturas adicionales (incluyendo algunas a vídeos de YouTube).
 
 _Léelo en otros idiomas:_
@@ -54,7 +54,7 @@ los datos.
 
 ## Algoritmos
 
-Un algoritmo es una especificación inequívoca de cómo resolver una clase de problemas. Es un conjunto de reglas que 
+Un algoritmo es una especificación inequívoca de cómo resolver una clase de problemas. Es un conjunto de reglas que
 definen con precisión una secuencia de operaciones.
 
 `P` - Principiante, `A` - Avanzado
@@ -231,7 +231,7 @@ npm test -- 'LinkedList'
 
 **Campo de juegos**
 
-Puede jugar con estructuras de datos y algoritmos en el archivo `./src/playground/playground.js` y escribir 
+Puede jugar con estructuras de datos y algoritmos en el archivo `./src/playground/playground.js` y escribir
 pruebas para ello en `./src/playground/__test__/playground.test.js`.
 
 A continuación, simplemente ejecute el siguiente comando para comprobar si el código funciona como se espera:
@@ -254,7 +254,7 @@ Orden de crecimiento de los algoritmos especificados en la notación O grande.
 
 Fuente: [Big O Cheat Sheet](http://bigocheatsheet.com/).
 
-A continuación se muestra la lista de algunas de las notaciones de Big O más utilizadas y sus comparaciones de rendimiento 
+A continuación se muestra la lista de algunas de las notaciones de Big O más utilizadas y sus comparaciones de rendimiento
 frente a diferentes tamaños de los datos de entrada.
 
 | Notación O grande | Cálculos para 10 elementos | Cálculos para 100 elementos | Cálculos para 1000 elementos |

README.it-IT.md

@@ -56,7 +56,7 @@ un insieme di regole che definiscono con precisione una sequenza di operazioni.
 
 * **Matematica**
   * `P` [Manipolazione dei Bit](src/algorithms/math/bits) - set/get/update/clear bits, moltiplicazione/divisione per due, gestire numeri negativi etc.
-  * `P` [Fattoriale](src/algorithms/math/factorial) 
+  * `P` [Fattoriale](src/algorithms/math/factorial)
   * `P` [Numeri di Fibonacci](src/algorithms/math/fibonacci) - classico e forma chiusa
   * `P` [Test di Primalità](src/algorithms/math/primality-test) (metodo del divisore)
   * `P` [Algoritmo di Euclide](src/algorithms/math/euclidean-algorithm) - trova il massimo comune divisore (MCD)
@@ -64,13 +64,13 @@ un insieme di regole che definiscono con precisione una sequenza di operazioni.
   * `P` [Crivello di Eratostene](src/algorithms/math/sieve-of-eratosthenes) - trova i numeri i primi fino al limite indicato
   * `P` [Potenza di due](src/algorithms/math/is-power-of-two) - controlla se il numero è una potenza di due
   * `P` [Triangolo di Pascal](src/algorithms/math/pascal-triangle)
-  * `P` [Numeri Complessi](src/algorithms/math/complex-number) - numeri complessi e operazioni 
+  * `P` [Numeri Complessi](src/algorithms/math/complex-number) - numeri complessi e operazioni
   * `P` [Radiante & Gradi](src/algorithms/math/radian) - conversione da radiante a gradi e viceversa
   * `P` [Potenza di un Numero](src/algorithms/math/fast-powering)
   * `A` [Partizione di un Intero](src/algorithms/math/integer-partition)
   * `A` [Radice Quadrata](src/algorithms/math/square-root) - Metodo di Newton
   * `A` [Algoritmo di Liu Hui π](src/algorithms/math/liu-hui) - calcolare π usando un poligono
-  * `A` [Trasformata Discreta di Fourier ](src/algorithms/math/fourier-transform) -decomporre una funzione di tempo (un segnale) nelle frequenze che lo compongono 
+  * `A` [Trasformata Discreta di Fourier ](src/algorithms/math/fourier-transform) -decomporre una funzione di tempo (un segnale) nelle frequenze che lo compongono
 * **Set**
   * `P` [Prodotto Cartesiano](src/algorithms/sets/cartesian-product) - moltiplicazione multipla di set
   * `P` [Fisher–Yates Shuffle](src/algorithms/sets/fisher-yates) - permutazione casuale di un sequenza finita
@@ -116,8 +116,8 @@ un insieme di regole che definiscono con precisione una sequenza di operazioni.
   * `P` [Ricerca in Profondità su Grafi](src/algorithms/graph/depth-first-search) (DFS)
   * `P` [Breadth-First Search su Grafi](src/algorithms/graph/breadth-first-search) (BFS)
   * `P` [Algoritmo di Kruskal](src/algorithms/graph/kruskal) - ricerca dell'Albero con Minima Distanza (MST) per grafi pesati unidirezionali
-  * `A` [Algoritmo di Dijkstra](src/algorithms/graph/dijkstra) - ricerca dei percorsi più breve per raggiungere tutti i vertici del grafo da un singolo vertice 
+  * `A` [Algoritmo di Dijkstra](src/algorithms/graph/dijkstra) - ricerca dei percorsi più breve per raggiungere tutti i vertici del grafo da un singolo vertice
-  * `A` [Algoritmo di Bellman-Ford](src/algorithms/graph/bellman-ford) - ricerca dei percorsi più breve per raggiungere tutti i vertici del grafo da un singolo vertice 
+  * `A` [Algoritmo di Bellman-Ford](src/algorithms/graph/bellman-ford) - ricerca dei percorsi più breve per raggiungere tutti i vertici del grafo da un singolo vertice
   * `A` [Algoritmo di Floyd-Warshall](src/algorithms/graph/floyd-warshall) -  ricerca dei percorsi più brevi tra tutte le coppie di vertici
   * `A` [Rivelamento dei Cicli](src/algorithms/graph/detect-cycle) - per grafici diretti e non diretti (basate su partizioni DFS e Disjoint Set)
   * `A` [Algoritmo di Prim](src/algorithms/graph/prim) - ricerca dell'Albero Ricoprente Minimo (MST) per grafi unidirezionali pesati
@@ -129,12 +129,12 @@ un insieme di regole che definiscono con precisione una sequenza di operazioni.
   * `A` [Componenti Fortemente Connessa](src/algorithms/graph/strongly-connected-components) - algoritmo di Kosaraju
   * `A` [Problema del Commesso Viaggiatore](src/algorithms/graph/travelling-salesman) - il percorso più breve che visita ogni città e ritorna alla città iniziale
 * **Crittografia**
-  * `P` [Hash Polinomiale](src/algorithms/cryptography/polynomial-hash) - Una funzione hash di rolling basata sul polinomio 
+  * `P` [Hash Polinomiale](src/algorithms/cryptography/polynomial-hash) - Una funzione hash di rolling basata sul polinomio
 * **Senza categoria**
   * `P` [Torre di Hanoi](src/algorithms/uncategorized/hanoi-tower)
   * `P` [Rotazione Matrice Quadrata](src/algorithms/uncategorized/square-matrix-rotation) - algoritmo in memoria
   * `P` [Jump Game](src/algorithms/uncategorized/jump-game) - backtracking, programmazione dinamica (top-down + bottom-up) ed esempre di greeedy
-  * `P` [Percorsi Unici](src/algorithms/uncategorized/unique-paths) - backtracking, programmazione dinamica and l'esempio del Triangolo di Pascal  
+  * `P` [Percorsi Unici](src/algorithms/uncategorized/unique-paths) - backtracking, programmazione dinamica and l'esempio del Triangolo di Pascal
   * `P` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - problema dell'acqua piovana in trappola(versione con programmazione dinamica e brute force)
   * `P` [Recursive Staircase](src/algorithms/uncategorized/recursive-staircase) - contare il numero di percorsi per arrivare in vetta(4 soluzioni)
   * `A` [Rompicapo delle Otto Regine](src/algorithms/uncategorized/n-queens)
@@ -151,14 +151,14 @@ un insieme di regole che definiscono con precisione una sequenza di operazioni.
   * `P` [Recursive Staircase](src/algorithms/uncategorized/recursive-staircase) - contare il numero di percorsi per arrivare in vetta
   * `A` [Massimo SubArray](src/algorithms/sets/maximum-subarray)
   * `A` [Problema del commesso viaggiatore](src/algorithms/graph/travelling-salesman) - il percorso più breve che visita ogni città e ritorna alla città iniziale
-  * `A` [Trasformata Discreta di Fourier](src/algorithms/math/fourier-transform) - scomporre la funzione (segnale) del tempo in frequenze che la compongono 
+  * `A` [Trasformata Discreta di Fourier](src/algorithms/math/fourier-transform) - scomporre la funzione (segnale) del tempo in frequenze che la compongono
 * **Greedy** - scegliere l'opzione migliore al momento d'eleborazione dell'algoritmo, senza alcuna considerazione per il futuro
   * `P` [Jump Game](src/algorithms/uncategorized/jump-game)
   * `A` [Problema dello Zaino di Knapsack](src/algorithms/sets/knapsack-problem)
   * `A` [Algoritmo di Dijkstra](src/algorithms/graph/dijkstra) - ricerca del percorso più breve tra tutti i vertici del grafo
-  * `A` [Algoritmo di Prim](src/algorithms/graph/prim) - ricerca del Minimo Albero Ricoprente per grafi pesati e unidirezionali 
+  * `A` [Algoritmo di Prim](src/algorithms/graph/prim) - ricerca del Minimo Albero Ricoprente per grafi pesati e unidirezionali
   * `A` [Kruskal’s Algorithm](src/algorithms/graph/kruskal) - finding Minimum Spanning Tree (MST) for weighted undirected graph
-* **Divide e Conquista** - divide il problema in piccole parti e risolve ogni parte 
+* **Divide e Conquista** - divide il problema in piccole parti e risolve ogni parte
   * `P` [Ricerca Binaria](src/algorithms/search/binary-search)
   * `P` [Torre di Hanoi](src/algorithms/uncategorized/hanoi-tower)
   * `P` [Triangolo di Pascal](src/algorithms/math/pascal-triangle)
@@ -186,7 +186,7 @@ un insieme di regole che definiscono con precisione una sequenza di operazioni.
   * `A` [Partizione di un Intero](src/algorithms/math/integer-partition)
   * `A` [Massimo SubArray](src/algorithms/sets/maximum-subarray)
   * `A` [Algoritmo di Bellman-Ford](src/algorithms/graph/bellman-ford) - ricerca del percorso più breve per tutti i vertici del grafo
-  * `A` [Algoritmo di Floyd-Warshall](src/algorithms/graph/floyd-warshall) - ricerca del percorso più breve tra tutte le coppie di vertici 
+  * `A` [Algoritmo di Floyd-Warshall](src/algorithms/graph/floyd-warshall) - ricerca del percorso più breve tra tutte le coppie di vertici
   * `A` [Espressioni Regolari](src/algorithms/string/regular-expression-matching)
 * **Backtracking** -  come la brute force, provate a generare tutte le soluzioni possibili, ma ogni volta che generate la prossima soluzione testate se soddisfa tutte le condizioni e solo allora continuare a generare soluzioni successive. Altrimenti, fate marcia indietro, e andate su un percorso diverso per trovare una soluzione. Normalmente si utilizza l'algoritmo DFS.
   * `P` [Jump Game](src/algorithms/uncategorized/jump-game)
@@ -228,10 +228,10 @@ npm test -- 'LinkedList'
 
 **Playground**
 
-Se vuoi puoi giocare le strutture dati e gli algoritmi nel file ./src/playground/playground.js` e 
+Se vuoi puoi giocare le strutture dati e gli algoritmi nel file ./src/playground/playground.js` e
 scrivere test nel file `./src/playground/__test__/playground.test.js`.
 
-Poi puoi semplicemente eseguire il seguente comando per testare quello che hai scritto : 
+Poi puoi semplicemente eseguire il seguente comando per testare quello che hai scritto :
 
 ```
 npm test -- 'playground'
@@ -243,9 +243,9 @@ npm test -- 'playground'
 
 [▶ Data Structures and Algorithms on YouTube](https://www.youtube.com/playlist?list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
 
-### Notazione Big O 
+### Notazione Big O
 
-* La notazione Big O* è usata per classificare algoritmi in base al tempo di esecuzione o ai 
+* La notazione Big O* è usata per classificare algoritmi in base al tempo di esecuzione o ai
 requisiti di spazio che crescono in base alla crescita dell'input .
 Nella grafico qua sotto puoi trovare gli ordini di crescita più comuni degli algoritmi usando la notazione Big O.
 

README.ja-JP.md

@@ -60,7 +60,7 @@ _Read this in other languages:_
 
 * **数学**
   * `B` [ビット操作](src/algorithms/math/bits) - set/get/update/clear bits, 2つの乗算/除算, 否定的にする. 等
-  * `B` [因果関係](src/algorithms/math/factorial) 
+  * `B` [因果関係](src/algorithms/math/factorial)
   * `B` [フィボナッチ数](src/algorithms/math/fibonacci) - クラシックとクローズドフォームのバージョン
   * `B` [素数性テスト](src/algorithms/math/primality-test) (trial division 方法)
   * `B` [ユークリッドアルゴリズム](src/algorithms/math/euclidean-algorithm) - 最大公約数を計算する (GCD)
@@ -118,7 +118,7 @@ _Read this in other languages:_
 * **グラフ**
   * `B` [深度優先検索](src/algorithms/graph/depth-first-search) (DFS)
   * `B` [幅優先検索](src/algorithms/graph/breadth-first-search) (BFS)
-  * `B` [Kruskalのアルゴリズム](src/algorithms/graph/kruskal) - 重み付き無向グラフの最小スパニングツリー（MST）の発見 
+  * `B` [Kruskalのアルゴリズム](src/algorithms/graph/kruskal) - 重み付き無向グラフの最小スパニングツリー（MST）の発見
   * `A` [Dijkstraアルゴリズム](src/algorithms/graph/dijkstra) - 単一の頂点からすべてのグラフ頂点への最短経路を見つける
   * `A` [Bellman-Fordアルゴリズム](src/algorithms/graph/bellman-ford) - 単一の頂点からすべてのグラフ頂点への最短経路を見つける
   * `A` [Floyd-Warshallアルゴリズム](src/algorithms/graph/floyd-warshall) - すべての頂点ペア間の最短経路を見つける

README.ko-KR.md

@@ -25,7 +25,7 @@ _Read this in other languages:_
 
 자료 구조는 데이터를 특정 방식으로 구성하고 저장함으로써 더 효율적으로
 접근하고 수정할 수 있게 해줍니다. 간단히 말해, 자료 구조는 데이터 값들,
-데이터 간의 관계, 그리고 데이터를 다룰 수 있는 함수와 작업의 모임입니다. 
+데이터 간의 관계, 그리고 데이터를 다룰 수 있는 함수와 작업의 모임입니다.
 
 
 `B` - 입문자, `A` - 숙련자
@@ -50,8 +50,8 @@ _Read this in other languages:_
 
 ## 알고리즘
 
-알고리즘은 어떤 종류의 문제를 풀 수 있는 정확한 방법이며, 
+알고리즘은 어떤 종류의 문제를 풀 수 있는 정확한 방법이며,
-일련의 작업을 정확하게 정의해 놓은 규칙들입니다. 
+일련의 작업을 정확하게 정의해 놓은 규칙들입니다.
 
 `B` - 입문자, `A` - 숙련자
 
@@ -59,7 +59,7 @@ _Read this in other languages:_
 
 * **Math**
   * `B` [Bit Manipulation](src/algorithms/math/bits) - set/get/update/clear bits, 2의 곱 / 나누기, 음수로 만들기 etc.
-  * `B` [팩토리얼](src/algorithms/math/factorial) 
+  * `B` [팩토리얼](src/algorithms/math/factorial)
   * `B` [피보나치 수](src/algorithms/math/fibonacci)
   * `B` [소수 판별](src/algorithms/math/primality-test) (trial division 방식)
   * `B` [유클리드 호제법](src/algorithms/math/euclidean-algorithm) - 최대공약수 (GCD)
@@ -126,7 +126,7 @@ _Read this in other languages:_
 * **Uncategorized**
   * `B` [하노이 탑](src/algorithms/uncategorized/hanoi-tower)
   * `B` [정방 행렬 회전](src/algorithms/uncategorized/square-matrix-rotation) - 제자리(in-place) 알고리즘
-  * `B` [점프 게임](src/algorithms/uncategorized/jump-game) - 백트래킹, 동적계획법 (top-down + bottom-up), 탐욕 알고리즘 예제 
+  * `B` [점프 게임](src/algorithms/uncategorized/jump-game) - 백트래킹, 동적계획법 (top-down + bottom-up), 탐욕 알고리즘 예제
   * `B` [Unique 경로](src/algorithms/uncategorized/unique-paths) - 백트래킹, 동적계획법, 파스칼 삼각형에 기반한 예제
   * `B` [빗물 담기 문제](src/algorithms/uncategorized/rain-terraces) - trapping rain water problem (동적계획법, 브루트포스 버전)
   * `A` [N-Queens 문제](src/algorithms/uncategorized/n-queens)

README.md

@@ -23,7 +23,7 @@ _Read this in other languages:_
 [_Türk_](README.tr-TR.md),
 [_Italiana_](README.it-IT.md)
 
-*☝ Note that this project is meant to be used for learning and researching purposes 
+*☝ Note that this project is meant to be used for learning and researching purposes
 only, and it is **not** meant to be used for production.*
 
 ## Data Structures
@@ -64,9 +64,9 @@ a set of rules that precisely define a sequence of operations.
 
 * **Math**
   * `B` [Bit Manipulation](src/algorithms/math/bits) - set/get/update/clear bits, multiplication/division by two, make negative etc.
-  * `B` [Factorial](src/algorithms/math/factorial) 
+  * `B` [Factorial](src/algorithms/math/factorial)
   * `B` [Fibonacci Number](src/algorithms/math/fibonacci) - classic and closed-form versions
-  * `B` [Prime Factors](src/algorithms/math/prime-factors) - finding prime factors and counting them using Hardy-Ramanujan's theorem  
+  * `B` [Prime Factors](src/algorithms/math/prime-factors) - finding prime factors and counting them using Hardy-Ramanujan's theorem
   * `B` [Primality Test](src/algorithms/math/primality-test) (trial division method)
   * `B` [Euclidean Algorithm](src/algorithms/math/euclidean-algorithm) - calculate the Greatest Common Divisor (GCD)
   * `B` [Least Common Multiple](src/algorithms/math/least-common-multiple) (LCM)
@@ -80,7 +80,7 @@ a set of rules that precisely define a sequence of operations.
   * `A` [Integer Partition](src/algorithms/math/integer-partition)
   * `A` [Square Root](src/algorithms/math/square-root) - Newton's method
   * `A` [Liu Hui π Algorithm](src/algorithms/math/liu-hui) - approximate π calculations based on N-gons
-  * `A` [Discrete Fourier Transform](src/algorithms/math/fourier-transform) - decompose a function of time (a signal) into the frequencies that make it up 
+  * `A` [Discrete Fourier Transform](src/algorithms/math/fourier-transform) - decompose a function of time (a signal) into the frequencies that make it up
 * **Sets**
   * `B` [Cartesian Product](src/algorithms/sets/cartesian-product) - product of multiple sets
   * `B` [Fisher–Yates Shuffle](src/algorithms/sets/fisher-yates) - random permutation of a finite sequence
@@ -143,11 +143,12 @@ a set of rules that precisely define a sequence of operations.
   * `B` [Caesar Cipher](src/algorithms/cryptography/caesar-cipher) - simple substitution cipher
 * **Machine Learning**
   * `B` [NanoNeuron](https://github.com/trekhleb/nano-neuron) - 7 simple JS functions that illustrate how machines can actually learn (forward/backward propagation)
+  * `B` [k-NN](src/algorithms/ml/knn) - k-nearest neighbors classification algorithm
 * **Uncategorized**
   * `B` [Tower of Hanoi](src/algorithms/uncategorized/hanoi-tower)
   * `B` [Square Matrix Rotation](src/algorithms/uncategorized/square-matrix-rotation) - in-place algorithm
-  * `B` [Jump Game](src/algorithms/uncategorized/jump-game) - backtracking, dynamic programming (top-down + bottom-up) and greedy examples 
+  * `B` [Jump Game](src/algorithms/uncategorized/jump-game) - backtracking, dynamic programming (top-down + bottom-up) and greedy examples
-  * `B` [Unique Paths](src/algorithms/uncategorized/unique-paths) - backtracking, dynamic programming and Pascal's Triangle based examples 
+  * `B` [Unique Paths](src/algorithms/uncategorized/unique-paths) - backtracking, dynamic programming and Pascal's Triangle based examples
   * `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - trapping rain water problem (dynamic programming and brute force versions)
   * `B` [Recursive Staircase](src/algorithms/uncategorized/recursive-staircase) - count the number of ways to reach to the top (4 solutions)
   * `A` [N-Queens Problem](src/algorithms/uncategorized/n-queens)

README.pl-PL.md

@@ -3,11 +3,11 @@
 [![CI](https://github.com/trekhleb/javascript-algorithms/workflows/CI/badge.svg)](https://github.com/trekhleb/javascript-algorithms/actions)
 [![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)
 
-To repozytorium zawiera wiele przykładów JavaScript opartych na 
+To repozytorium zawiera wiele przykładów JavaScript opartych na
 znanych algorytmach i strukturach danych.
 
 Każdy algorytm i struktura danych zawiera osobny plik README
-wraz z powiązanymi wyjaśnieniami i odnośnikami do dalszego czytania 
+wraz z powiązanymi wyjaśnieniami i odnośnikami do dalszego czytania
 (włącznie z tymi do YouTube videos).
 
 _Read this in other languages:_
@@ -25,10 +25,10 @@ _Read this in other languages:_
 
 ## Struktury Danych
 
-Struktura danych to sposób uporządkowania i przechowywania informacji w 
+Struktura danych to sposób uporządkowania i przechowywania informacji w
 komputerze żeby mogłaby być sprawnie dostępna i efektywnie zmodyfikowana.
-Dokładniej, struktura danych jest zbiorem wartości danych, relacjami 
+Dokładniej, struktura danych jest zbiorem wartości danych, relacjami
-pomiędzy nimi, zadaniami lub działaniami, które mogą dotyczyć danych. 
+pomiędzy nimi, zadaniami lub działaniami, które mogą dotyczyć danych.
 
 `B` - Początkujący, `A` - Zaawansowany
 
@@ -52,8 +52,8 @@ pomiędzy nimi, zadaniami lub działaniami, które mogą dotyczyć danych.
 
 ## Algorytmy
 
-Algorytm jest to skończony ciąg jasno zdefiniowanych czynności, koniecznych 
+Algorytm jest to skończony ciąg jasno zdefiniowanych czynności, koniecznych
-do wykonania pewnego rodzaju zadań. Sposób postępowania prowadzący do 
+do wykonania pewnego rodzaju zadań. Sposób postępowania prowadzący do
 rozwiązania problemu.
 
 `B` - Początkujący, `A` - Zaawansowany
@@ -62,7 +62,7 @@ rozwiązania problemu.
 
 * **Matematyka**
   * `B` [Manipulacja Bitami](src/algorithms/math/bits) - ustaw / uzyskaj / aktualizuj / usuwaj bity, mnożenie / dzielenie przez dwa, tworzenie negatywów itp.
-  * `B` [Silna](src/algorithms/math/factorial) 
+  * `B` [Silna](src/algorithms/math/factorial)
   * `B` [Ciąg Fibonacciego](src/algorithms/math/fibonacci)
   * `B` [Test Pierwszorzędności](src/algorithms/math/primality-test) (metoda podziału na próby)
   * `B` [Algorytm Euclideana](src/algorithms/math/euclidean-algorithm) - obliczyć Największy Wspólny Dzielnik (GCD)
@@ -81,9 +81,9 @@ rozwiązania problemu.
   * `A` [Najdłuższa Wspólna Podsekwencja](src/algorithms/sets/longest-common-subsequence) (LCS)
   * `A` [Najdłuższa Wzrostająca Podsekwencja](src/algorithms/sets/longest-increasing-subsequence)
   * `A` [Najkrótsza Wspólna Supersekwencja](src/algorithms/sets/shortest-common-supersequence) (SCS)
-  * `A` [Problem Knapsacka](src/algorithms/sets/knapsack-problem) - "0/1" i "Rozwiązany" 
+  * `A` [Problem Knapsacka](src/algorithms/sets/knapsack-problem) - "0/1" i "Rozwiązany"
   * `A` [Maksymalna Podtablica](src/algorithms/sets/maximum-subarray) - "Metoda Siłowa" i "Dynamiczne Programowanie" (Kadane-a) wersje
-  * `A` [Suma Kombinacji](src/algorithms/sets/combination-sum) - 
+  * `A` [Suma Kombinacji](src/algorithms/sets/combination-sum) -
 znajdź wszystkie kombinacje, które tworzą określoną sumę
 * **Łańcuchy**
   * `B` [Odległość Hamminga](src/algorithms/string/hamming-distance) - liczba pozycji, w których symbole są różne
@@ -120,26 +120,26 @@ znajdź wszystkie kombinacje, które tworzą określoną sumę
   * `A` [Algorytm Floyd-Warshalla](src/algorithms/graph/floyd-warshall) - znajdź najkrótsze ścieżki między wszystkimi parami wierzchołków
   * `A` [Detect Cycle](src/algorithms/graph/detect-cycle) - zarówno dla wykresów skierowanych, jak i nieukierunkowanych(wersje oparte na DFS i Rozłączny Zestaw)
   * `A` [Algorytm Prima](src/algorithms/graph/prim) - znalezienie Minimalnego Drzewa Opinającego (MST) dla ważonego nieukierunkowanego wykresu
-  * `A` [Sortowanie Topologiczne](src/algorithms/graph/topological-sorting) - metoda DFS 
+  * `A` [Sortowanie Topologiczne](src/algorithms/graph/topological-sorting) - metoda DFS
   * `A` [Punkty Artykulacji](src/algorithms/graph/articulation-points) - Algorytm Tarjana (oparty o DFS)
-  * `A` [Mosty](src/algorithms/graph/bridges) - Oparty na algorytmie DFS 
+  * `A` [Mosty](src/algorithms/graph/bridges) - Oparty na algorytmie DFS
   * `A` [Ścieżka Euleriana i Obwód Euleriana](src/algorithms/graph/eulerian-path) - Algorytm Fleurya - Odwiedź każdą krawędź dokładnie raz
   * `A` [Cykl Hamiltoniana](src/algorithms/graph/hamiltonian-cycle) - Odwiedź każdy wierzchołek dokładnie raz
-  * `A` [Silnie Połączone Komponenty](src/algorithms/graph/strongly-connected-components) - Algorytm Kosaraja 
+  * `A` [Silnie Połączone Komponenty](src/algorithms/graph/strongly-connected-components) - Algorytm Kosaraja
   * `A` [Travelling Salesman Problem](src/algorithms/graph/travelling-salesman) - najkrótsza ścieżka która odwiedza każde miasto i wraca miasta początkującego
 * **Niezkategorizowane**
   * `B` [Wieża Hanoi](src/algorithms/uncategorized/hanoi-tower)
   * `B` [Kwadratowa Matryca Obrotu](src/algorithms/uncategorized/square-matrix-rotation) - algorytm w miejscu
-  * `B` [Jump Game](src/algorithms/uncategorized/jump-game) - cofanie, dynamiczne programowanie (od góry do dołu + od dołu do góry) i przykłady chciwego  
+  * `B` [Jump Game](src/algorithms/uncategorized/jump-game) - cofanie, dynamiczne programowanie (od góry do dołu + od dołu do góry) i przykłady chciwego
   * `B` [Unikatowe Ścieżki](src/algorithms/uncategorized/unique-paths) - cofanie, dynamiczne programowanie i przykłady oparte na Trójkącie Pascala
   * `A` [Problem N-Queens](src/algorithms/uncategorized/n-queens)
   * `A` [Knight's Tour](src/algorithms/uncategorized/knight-tour)
 
 ### Algorytmy według paradygmatu
 
-Paradygmat algorytmiczny jest ogólną metodą lub podejściem, które jest 
+Paradygmat algorytmiczny jest ogólną metodą lub podejściem, które jest
-podstawą projektowania klasy algorytmów. Jest abstrakcją wyższą niż 
+podstawą projektowania klasy algorytmów. Jest abstrakcją wyższą niż
-pojęcie algorytmu, podobnie jak algorytm jest abstrakcją wyższą niż 
+pojęcie algorytmu, podobnie jak algorytm jest abstrakcją wyższą niż
 program komputerowy.
 
 * **Metoda Siłowa** - Sprawdza wszystkie możliwosci i wybiera  najlepsze rozwiązanie.
@@ -149,7 +149,7 @@ program komputerowy.
 * **Chciwy** - wybierz najlepszą opcję w obecnym czasie, bez względu na przyszłość
   * `B` [Jump Game](src/algorithms/uncategorized/jump-game)
   * `A` [Niezwiązany Problem Knapsacka ](src/algorithms/sets/knapsack-problem)
-  * `A` [Algorytm Dijkstry](src/algorithms/graph/dijkstra) - 
+  * `A` [Algorytm Dijkstry](src/algorithms/graph/dijkstra) -
 znalezienie najkrótszej ścieżki do wszystkich wierzchołków grafu
   * `A` [Algorytm Prima](src/algorithms/graph/prim) - znalezienie Minimalnego Drzewa Opinającego (MST) dla ważonego nieukierunkowanego wykresu
   * `A` [Algorytm Kruskala](src/algorithms/graph/kruskal) - znalezienie Minimalnego Drzewa Opinającego (MST) dla ważonego nieukierunkowanego wykresu
@@ -178,7 +178,7 @@ znalezienie najkrótszej ścieżki do wszystkich wierzchołków grafu
   * `A` [Partycja Całkowita](src/algorithms/math/integer-partition)
   * `A` [Maksymalne Podtablice](src/algorithms/sets/maximum-subarray)
   * `A` [Algorytm Bellman-Forda](src/algorithms/graph/bellman-ford) - znalezienie najkrótszej ścieżki wszystkich wierzchołków wykresu
-  * `A` [Algorytm Floyd-Warshalla](src/algorithms/graph/floyd-warshall) - 
+  * `A` [Algorytm Floyd-Warshalla](src/algorithms/graph/floyd-warshall) -
 znajdź najkrótsze ścieżki między wszystkimi parami wierzchołków
   * `A` [Dopasowanie Wyrażeń Regularnych](src/algorithms/string/regular-expression-matching)
 * **Algorytm z nawrotami** - podobny do metody siłowej, próbuje wygenerować wszystkie możliwe rozwiązania, jednak za każdym razem generujesz następne rozwiązanie które testujesz
@@ -192,7 +192,7 @@ jeżeli zaspokaja wszystkie warunki, tylko wtedy generuje kolejne rozwiązania.
 * **Metoda Podziału i Ograniczeń** - Pamięta o niskonakładowym rozwiązaniu znalezionym na każdym etapie szukania nawrotu,
 używa kosztu niskonakładowego kosztu, które dotychczas zostało znalezione jako niska granica najmniejszego kosztu
 do rozwiązanie problemu, aby odrzucić cząstkowe rozwiązania o kosztach większych niż niskonakładowe
-rozwiązanie znalezione do tej pory. 
+rozwiązanie znalezione do tej pory.
 Zazwyczan trajektoria BFS, w połączeniu z trajektorią Przeszukiwania W Głąb (DFS) drzewa przestrzeni stanów jest użyte.
 
 ## Jak używać repozytorium
@@ -225,7 +225,7 @@ npm test -- 'LinkedList'
 Możesz pociwiczyć ze strukturą danych i algorytmami w `./src/playground/playground.js` zakartotekuj i napisz
 testy do tego w `./src/playground/__test__/playground.test.js`.
 
-Następnie uruchom następującą komendę w celu przetestowania czy twoje kod działa według oczekiwań: 
+Następnie uruchom następującą komendę w celu przetestowania czy twoje kod działa według oczekiwań:
 
 ```
 npm test -- 'playground'
@@ -239,7 +239,7 @@ npm test -- 'playground'
 
 ### Big O Notacja
 
-Kolejność wzrastania algorytmów według Big O notacji. 
+Kolejność wzrastania algorytmów według Big O notacji.
 
 ![Big O grafy](./assets/big-o-graph.png)
 

README.pt-BR.md

@@ -4,7 +4,7 @@
 [![codecov](https://codecov.io/gh/trekhleb/javascript-algorithms/branch/master/graph/badge.svg)](https://codecov.io/gh/trekhleb/javascript-algorithms)
 
 Este repositório contém exemplos baseados em JavaScript de muitos
-algoritmos e estruturas de dados populares. 
+algoritmos e estruturas de dados populares.
 
 Cada algoritmo e estrutura de dado possui seu próprio README
 com explicações relacionadas e links para leitura adicional (incluindo
@@ -61,7 +61,7 @@ um conjunto de regras que define precisamente uma sequência de operações.
 
 * **Matemática**
   * `B` [Manipulação Bit](src/algorithms/math/bits) - set/get/update/clear bits, multiplicação / divisão por dois, tornar negativo etc.
-  * `B` [Fatorial](src/algorithms/math/factorial) 
+  * `B` [Fatorial](src/algorithms/math/factorial)
   * `B` [Número de Fibonacci](src/algorithms/math/fibonacci)
   * `B` [Teste de Primalidade](src/algorithms/math/primality-test) (método de divisão experimental)
   * `B` [Algoritmo Euclidiano](src/algorithms/math/euclidean-algorithm) - calcular o maior divisor comum (GCD)
@@ -119,7 +119,7 @@ um conjunto de regras que define precisamente uma sequência de operações.
   * `A` [Floyd-Warshall Algorithm](src/algorithms/graph/floyd-warshall) - encontrar caminhos mais curtos entre todos os pares de vértices
   * `A` [Detect Cycle](src/algorithms/graph/detect-cycle) - para gráficos direcionados e não direcionados (versões baseadas em DFS e Conjunto Disjuntivo)
   * `A` [Prim’s Algorithm](src/algorithms/graph/prim) - encontrando Árvore Mínima de Abrangência (MST) para grafo não direcionado ponderado
-  * `A` [Topological Sorting](src/algorithms/graph/topological-sorting) - Métodos DFS 
+  * `A` [Topological Sorting](src/algorithms/graph/topological-sorting) - Métodos DFS
   * `A` [Articulation Points](src/algorithms/graph/articulation-points) -O algoritmo de Tarjan (baseado em DFS)
   * `A` [Bridges](src/algorithms/graph/bridges) - Algoritmo baseado em DFS
   * `A` [Eulerian Path and Eulerian Circuit](src/algorithms/graph/eulerian-path) - Algoritmo de Fleury - Visite todas as bordas exatamente uma vez

README.ru-RU.md

@@ -56,7 +56,7 @@ _Читать на других языках:_
 
 * **Математика**
   * `B` [Битовые манипуляции](src/algorithms/math/bits) — получение/запись/сброс/обновление битов, умножение/деление на 2, сделать отрицательным и т.п.
-  * `B` [Факториал](src/algorithms/math/factorial) 
+  * `B` [Факториал](src/algorithms/math/factorial)
   * `B` [Числа Фибоначчи](src/algorithms/math/fibonacci) — классическое решение, решение в замкнутой форме
   * `B` [Тест простоты](src/algorithms/math/primality-test) (метод пробного деления)
   * `B` [Алгоритм Евклида](src/algorithms/math/euclidean-algorithm) — нахождение наибольшего общего делителя (НОД)
@@ -70,7 +70,7 @@ _Читать на других языках:_
   * `A` [Разбиение числа](src/algorithms/math/integer-partition)
   * `A` [Квадратный корень](src/algorithms/math/square-root) — метод Ньютона
   * `A` [Алгоритм Лю Хуэя](src/algorithms/math/liu-hui) — расчёт числа π с заданной точностью методом вписанных правильных многоугольников
-  * `A` [Дискретное преобразование Фурье](src/algorithms/math/fourier-transform) — разложение временной функции (сигнала) на частотные составляющие 
+  * `A` [Дискретное преобразование Фурье](src/algorithms/math/fourier-transform) — разложение временной функции (сигнала) на частотные составляющие
 * **Множества**
   * `B` [Декартово произведение](src/algorithms/sets/cartesian-product) — результат перемножения множеств
   * `B` [Тасование Фишера — Йетса](src/algorithms/sets/fisher-yates) — создание случайных перестановок конечного множества
@@ -135,7 +135,7 @@ _Читать на других языках:_
 * **Прочие алгоритмы**
   * `B` [Ханойская башня](src/algorithms/uncategorized/hanoi-tower)
   * `B` [Поворот квадратной матрицы](src/algorithms/uncategorized/square-matrix-rotation) — используется дополнительная память
-  * `B` [Прыжки](src/algorithms/uncategorized/jump-game) — на основе бэктрекинга, динамического программирования (сверху-вниз + снизу-вверх) и жадных алгоритмов 
+  * `B` [Прыжки](src/algorithms/uncategorized/jump-game) — на основе бэктрекинга, динамического программирования (сверху-вниз + снизу-вверх) и жадных алгоритмов
   * `B` [Поиск уникальных путей](src/algorithms/uncategorized/unique-paths) — на основе бэктрекинга, динамического программирования и треугольника Паскаля
   * `B` [Подсчёт дождевой воды](src/algorithms/uncategorized/rain-terraces) — на основе перебора и динамического программирования
   * `B` [Задача о рекурсивной лестнице](src/algorithms/uncategorized/recursive-staircase) — подсчёт количества путей, по которым можно достичь верха лестницы (4 способа)
@@ -153,7 +153,7 @@ _Читать на других языках:_
   * `A` [Максимальный подмассив](src/algorithms/sets/maximum-subarray)
   * `A` [Задача коммивояжёра](src/algorithms/graph/travelling-salesman) — кратчайший маршрут, проходящий через указанные города с последующим возвратом в исходный город
   * `A` [Дискретное преобразование Фурье](src/algorithms/math/fourier-transform) — разложение временной функции (сигнала) на частотные составляющие
-* **Жадные алгоритмы** — принятие локально оптимальных решений с учётом допущения об оптимальности конечного решения 
+* **Жадные алгоритмы** — принятие локально оптимальных решений с учётом допущения об оптимальности конечного решения
   * `B` [Прыжки](src/algorithms/uncategorized/jump-game)
   * `A` [Задача о неограниченном рюкзаке](src/algorithms/sets/knapsack-problem)
   * `A` [Алгоритм Дейкстры](src/algorithms/graph/dijkstra) — нахождение кратчайших путей от одной из вершин графа до всех остальных
@@ -228,7 +228,7 @@ npm test -- 'LinkedList'
 
 **Песочница**
 
-Вы можете экспериментировать с алгоритмами и структурами данных в файле `./src/playground/playground.js` 
+Вы можете экспериментировать с алгоритмами и структурами данных в файле `./src/playground/playground.js`
 (файл `./src/playground/__test__/playground.test.js` предназначен для написания тестов).
 
 Для проверки работоспособности вашего кода используйте команду:

README.tr-TR.md

@@ -6,8 +6,8 @@
 Bu repository JavaScript'e ait popüler
 algoritma ve veri yapılarını içermektedir.
 
-Her bir algoritma ve veri yapısı kendine 
+Her bir algoritma ve veri yapısı kendine
-ait açıklama ve videoya sahip README dosyası içerir. 
+ait açıklama ve videoya sahip README dosyası içerir.
 
 _Read this in other languages:_
 [_简体中文_](README.zh-CN.md),
@@ -21,7 +21,7 @@ _Read this in other languages:_
 [_Русский_](README.ru-RU.md),
 [_Italiana_](README.it-IT.md)
 
-*☝ Not, bu proje araştırma ve öğrenme amacı ile yapılmış 
+*☝ Not, bu proje araştırma ve öğrenme amacı ile yapılmış
 olup üretim için **yaplılmamıştır**.*
 
 ## Veri Yapıları
@@ -63,7 +63,7 @@ bir işlem dizisini kesin olarak tanımlayan bir dizi kural.
 
 * **Matematik**
   * `B` [Bit Manipülasyonu](src/algorithms/math/bits) - set/get/update/clear bits, multiplication/division by two, make negative etc.
-  * `B` [Faktöriyel](src/algorithms/math/factorial) 
+  * `B` [Faktöriyel](src/algorithms/math/factorial)
   * `B` [Fibonacci Sayısı](src/algorithms/math/fibonacci) - klasik ve kapalı-form versiyonları
   * `B` [Asallık Testi](src/algorithms/math/primality-test) (trial division method)
   * `B` [Öklid Algoritması](src/algorithms/math/euclidean-algorithm) - En büyük ortak bölen hesaplama (EBOB)
@@ -143,8 +143,8 @@ bir işlem dizisini kesin olarak tanımlayan bir dizi kural.
 * **Kategoriye Ayrılmayanlar**
   * `B` [Tower of Hanoi](src/algorithms/uncategorized/hanoi-tower)
   * `B` [Square Matrix Rotation](src/algorithms/uncategorized/square-matrix-rotation) - in-place algorithm
-  * `B` [Jump Game](src/algorithms/uncategorized/jump-game) - backtracking, dynamic programming (top-down + bottom-up) and greedy examples 
+  * `B` [Jump Game](src/algorithms/uncategorized/jump-game) - backtracking, dynamic programming (top-down + bottom-up) and greedy examples
-  * `B` [Unique Paths](src/algorithms/uncategorized/unique-paths) - backtracking, dynamic programming and Pascal's Triangle based examples 
+  * `B` [Unique Paths](src/algorithms/uncategorized/unique-paths) - backtracking, dynamic programming and Pascal's Triangle based examples
   * `B` [Rain Terraces](src/algorithms/uncategorized/rain-terraces) - trapping rain water problem (dynamic programming and brute force versions)
   * `B` [Recursive Staircase](src/algorithms/uncategorized/recursive-staircase) - tepeye ulaşmanın yollarını sayma (4 çözüm)
   * `A` [N-Queens Problem](src/algorithms/uncategorized/n-queens)
@@ -152,8 +152,8 @@ bir işlem dizisini kesin olarak tanımlayan bir dizi kural.
 
 ### Algoritmik Paradigma
 
-Algoritmik paradigma, bir sınıfın tasarımının altında yatan genel bir yöntem veya yaklaşımdır. 
+Algoritmik paradigma, bir sınıfın tasarımının altında yatan genel bir yöntem veya yaklaşımdır.
-Algoritma dizayn tekniği olarak düşünülebilir. Her bir altproblemi (subproblem) asıl problemle 
+Algoritma dizayn tekniği olarak düşünülebilir. Her bir altproblemi (subproblem) asıl problemle
 benzerlik gösteren problemlere uygulanabilir.
 
 * **Brute Force** - mümkün olan tüm çözümleri tara ve en iyisini seç
@@ -198,7 +198,7 @@ benzerlik gösteren problemlere uygulanabilir.
   * `A` [Maximum Subarray](src/algorithms/sets/maximum-subarray)
   * `A` [Bellman-Ford Algorithm](src/algorithms/graph/bellman-ford) - tüm grafik köşelerine giden en kısa yolu bulmak
   * `A` [Floyd-Warshall Algorithm](src/algorithms/graph/floyd-warshall) - tüm köşe çiftleri arasındaki en kısa yolları bulun
-  * `A` [Regular Expression Matching](src/algorithms/string/regular-expression-matching) 
+  * `A` [Regular Expression Matching](src/algorithms/string/regular-expression-matching)
 * **Backtracking** - brute forceye benzer, mümkün tüm sonuçları tara, ancak bir sonraki çözümü her ürettiğinizde test edersiniz
 tüm koşulları karşılıyorsa ve ancak o zaman sonraki çözümleri üretmeye devam edin. Aksi takdirde, geri dönün ve farklı bir çözüm arayın(?).
 Normally the DFS traversal of state-space is being used.
@@ -242,7 +242,7 @@ npm test -- 'LinkedList'
 
 **Deneme Alanı**
 
-data-structures ve algorithms içerisinde `./src/playground/playground.js` 
+data-structures ve algorithms içerisinde `./src/playground/playground.js`
 yazarak `./src/playground/__test__/playground.test.js` için test edebilirsin.
 
 
@@ -310,4 +310,4 @@ Altta Big O notations ve farklı input boyutlarına karşın yapılmış perform
 
 ## Projeyi Destekleme
 
-Bu projeyi buradan destekleyebilirsiniz ❤️️ [GitHub](https://github.com/sponsors/trekhleb) veya ❤️️ [Patreon](https://www.patreon.com/trekhleb).          
+Bu projeyi buradan destekleyebilirsiniz ❤️️ [GitHub](https://github.com/sponsors/trekhleb) veya ❤️️ [Patreon](https://www.patreon.com/trekhleb).

jest.config.js

@@ -25,4 +25,14 @@ module.exports = {
   // It is reflected in properties such as location.href.
   // @see: https://github.com/facebook/jest/issues/6769
   testURL: 'http://localhost/',
+
+  // @see: https://jestjs.io/docs/en/configuration#coveragethreshold-object
+  coverageThreshold: {
+    global: {
+      statements: 100,
+      branches: 95,
+      functions: 100,
+      lines: 100,
+    },
+  },
 };

src/algorithms/ml/knn/README.md

@@ -0,0 +1,41 @@
+# k-Nearest Neighbors Algorithm
+
+The **k-nearest neighbors algorithm (k-NN)** is a supervised Machine Learning algorithm. It's a classification algorithm, determining the class of a sample vector using a sample data.
+
+In k-NN classification, the output is a class membership. An object is classified by a plurality vote of its neighbors, with the object being assigned to the class most common among its `k` nearest neighbors (`k` is a positive integer, typically small). If `k = 1`, then the object is simply assigned to the class of that single nearest neighbor.
+
+The idea is to calculate the similarity between two data points on the basis of a distance metric. [Euclidean distance](https://en.wikipedia.org/wiki/Euclidean_distance) is used mostly for this task.
+
+![Euclidean distance between two points](https://upload.wikimedia.org/wikipedia/commons/5/55/Euclidean_distance_2d.svg)
+
+_Image source: [Wikipedia](https://en.wikipedia.org/wiki/Euclidean_distance)_
+
+The algorithm is as follows:
+
+1. Check for errors like invalid data/labels.
+2. Calculate the euclidean distance of all the data points in training data with the classification point
+3. Sort the distances of points along with their classes in ascending order
+4. Take the initial `K` classes and find the mode to get the most similar class
+5. Report the most similar class
+
+Here is a visualization of k-NN classification for better understanding:
+
+![KNN Visualization 1](https://upload.wikimedia.org/wikipedia/commons/e/e7/KnnClassification.svg)
+
+_Image source: [Wikipedia](https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm)_
+
+The test sample (green dot) should be classified either to blue squares or to red triangles. If `k = 3` (solid line circle) it is assigned to the red triangles because there are `2` triangles and only `1` square inside the inner circle. If `k = 5` (dashed line circle) it is assigned to the blue squares (`3` squares vs. `2` triangles inside the outer circle).
+
+Another k-NN classification example:
+
+![KNN Visualization 2](https://media.geeksforgeeks.org/wp-content/uploads/graph2-2.png)
+
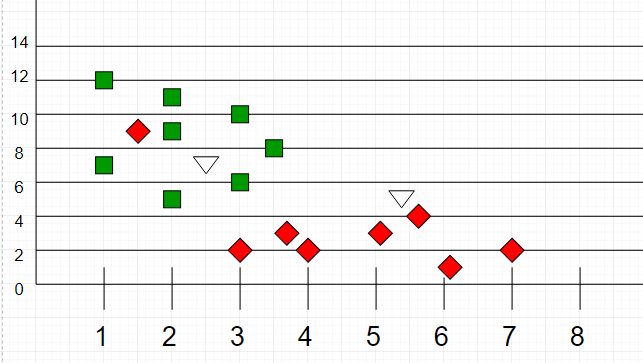
+_Image source: [GeeksForGeeks](https://media.geeksforgeeks.org/wp-content/uploads/graph2-2.png)_
+
+Here, as we can see, the classification of unknown points will be judged by their proximity to other points.
+
+It is important to note that `K` is preferred to have odd values in order to break ties. Usually `K` is taken as `3` or `5`.
+
+## References
+
+- [k-nearest neighbors algorithm on Wikipedia](https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm)

src/algorithms/ml/knn/__test__/knn.test.js

@@ -0,0 +1,71 @@
+import kNN from '../kNN';
+
+describe('kNN', () => {
+  it('should throw an error on invalid data', () => {
+    expect(() => {
+      kNN();
+    }).toThrowError('Either dataSet or labels or toClassify were not set');
+  });
+
+  it('should throw an error on invalid labels', () => {
+    const noLabels = () => {
+      kNN([[1, 1]]);
+    };
+    expect(noLabels).toThrowError('Either dataSet or labels or toClassify were not set');
+  });
+
+  it('should throw an error on not giving classification vector', () => {
+    const noClassification = () => {
+      kNN([[1, 1]], [1]);
+    };
+    expect(noClassification).toThrowError('Either dataSet or labels or toClassify were not set');
+  });
+
+  it('should throw an error on not giving classification vector', () => {
+    const inconsistent = () => {
+      kNN([[1, 1]], [1], [1]);
+    };
+    expect(inconsistent).toThrowError('Inconsistent vector lengths');
+  });
+
+  it('should find the nearest neighbour', () => {
+    let dataSet;
+    let labels;
+    let toClassify;
+    let expectedClass;
+
+    dataSet = [[1, 1], [2, 2]];
+    labels = [1, 2];
+    toClassify = [1, 1];
+    expectedClass = 1;
+    expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass);
+
+    dataSet = [[1, 1], [6, 2], [3, 3], [4, 5], [9, 2], [2, 4], [8, 7]];
+    labels = [1, 2, 1, 2, 1, 2, 1];
+    toClassify = [1.25, 1.25];
+    expectedClass = 1;
+    expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass);
+
+    dataSet = [[1, 1], [6, 2], [3, 3], [4, 5], [9, 2], [2, 4], [8, 7]];
+    labels = [1, 2, 1, 2, 1, 2, 1];
+    toClassify = [1.25, 1.25];
+    expectedClass = 2;
+    expect(kNN(dataSet, labels, toClassify, 5)).toBe(expectedClass);
+  });
+
+  it('should find the nearest neighbour with equal distances', () => {
+    const dataSet = [[0, 0], [1, 1], [0, 2]];
+    const labels = [1, 3, 3];
+    const toClassify = [0, 1];
+    const expectedClass = 3;
+    expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass);
+  });
+
+  it('should find the nearest neighbour in 3D space', () => {
+    const dataSet = [[0, 0, 0], [0, 1, 1], [0, 0, 2]];
+    const labels = [1, 3, 3];
+    const toClassify = [0, 0, 1];
+    const expectedClass = 3;
+    expect(kNN(dataSet, labels, toClassify)).toBe(expectedClass);
+  });
+});

src/algorithms/ml/knn/kNN.js

@@ -0,0 +1,77 @@
+/**
+ * Calculates calculate the euclidean distance between 2 vectors.
+ *
+ * @param {number[]} x1
+ * @param {number[]} x2
+ * @returns {number}
+ */
+function euclideanDistance(x1, x2) {
+  // Checking for errors.
+  if (x1.length !== x2.length) {
+    throw new Error('Inconsistent vector lengths');
+  }
+  // Calculate the euclidean distance between 2 vectors and return.
+  let squaresTotal = 0;
+  for (let i = 0; i < x1.length; i += 1) {
+    squaresTotal += (x1[i] - x2[i]) ** 2;
+  }
+  return Number(Math.sqrt(squaresTotal).toFixed(2));
+}
+
+/**
+ * Classifies the point in space based on k-nearest neighbors algorithm.
+ *
+ * @param {number[][]} dataSet - array of data points, i.e. [[0, 1], [3, 4], [5, 7]]
+ * @param {number[]} labels - array of classes (labels), i.e. [1, 1, 2]
+ * @param {number[]} toClassify - the point in space that needs to be classified, i.e. [5, 4]
+ * @param {number} k - number of nearest neighbors which will be taken into account (preferably odd)
+ * @return {number} - the class of the point
+ */
+export default function kNN(
+  dataSet,
+  labels,
+  toClassify,
+  k = 3,
+) {
+  if (!dataSet || !labels || !toClassify) {
+    throw new Error('Either dataSet or labels or toClassify were not set');
+  }
+
+  // Calculate distance from toClassify to each point for all dimensions in dataSet.
+  // Store distance and point's label into distances list.
+  const distances = [];
+  for (let i = 0; i < dataSet.length; i += 1) {
+    distances.push({
+      dist: euclideanDistance(dataSet[i], toClassify),
+      label: labels[i],
+    });
+  }
+
+  // Sort distances list (from closer point to further ones).
+  // Take initial k values, count with class index
+  const kNearest = distances.sort((a, b) => {
+    if (a.dist === b.dist) {
+      return 0;
+    }
+    return a.dist < b.dist ? -1 : 1;
+  }).slice(0, k);
+
+  // Count the number of instances of each class in top k members.
+  const labelsCounter = {};
+  let topClass = 0;
+  let topClassCount = 0;
+  for (let i = 0; i < kNearest.length; i += 1) {
+    if (kNearest[i].label in labelsCounter) {
+      labelsCounter[kNearest[i].label] += 1;
+    } else {
+      labelsCounter[kNearest[i].label] = 1;
+    }
+    if (labelsCounter[kNearest[i].label] > topClassCount) {
+      topClassCount = labelsCounter[kNearest[i].label];
+      topClass = kNearest[i].label;
+    }
+  }
+
+  // Return the class with highest count.
+  return topClass;
+}

src/algorithms/sorting/bubble-sort/README.md

@@ -1,11 +1,14 @@
 # Bubble Sort
 
-Bubble sort, sometimes referred to as sinking sort, is a 
+_Read this in other languages:_
-simple sorting algorithm that repeatedly steps through 
+[_Português_](README.pt-BR.md)
-the list to be sorted, compares each pair of adjacent 
+
-items and swaps them if they are in the wrong order 
+Bubble sort, sometimes referred to as sinking sort, is a
+simple sorting algorithm that repeatedly steps through
+the list to be sorted, compares each pair of adjacent
+items and swaps them if they are in the wrong order
 (ascending or descending arrangement). The pass through
-the list is repeated until no swaps are needed, which 
+the list is repeated until no swaps are needed, which
 indicates that the list is sorted.
 
 ![Algorithm Visualization](https://upload.wikimedia.org/wikipedia/commons/c/c8/Bubble-sort-example-300px.gif)

src/algorithms/sorting/bubble-sort/README.pt-BR.md

@@ -0,0 +1,17 @@
+# Bubble Sort
+
+O bubble sort, ou ordenação por flutuação (literalmente "por bolha"), é um algoritmo de ordenação dos mais simples. A ideia é percorrer o vetor diversas vezes, e a cada passagem fazer flutuar para o topo o maior elemento da sequência. Essa movimentação lembra a forma como as bolhas em um tanque de água procuram seu próprio nível, e disso vem o nome do algoritmo.
+
+![Algorithm Visualization](https://upload.wikimedia.org/wikipedia/commons/c/c8/Bubble-sort-example-300px.gif)
+
+## Complexity
+
+| Name                  | Best            | Average             | Worst               | Memory    | Stable    | Comments  |
+| --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
+| **Bubble sort**       | n               | n<sup>2</sup>       | n<sup>2</sup>       | 1         | Yes       |           |
+
+## References
+
+- [Wikipedia](https://pt.wikipedia.org/wiki/Bubble_sort)
+- [YouTube](https://www.youtube.com/watch?v=6Gv8vg0kcHc&index=27&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
+

src/data-structures/doubly-linked-list/README.zh-CN.md

@@ -51,7 +51,7 @@ Remove(head, value)
     return true
   end if
   n ← head.next
-  while n = ø and value = n.value
+  while n = ø and value !== n.value
     n ← n.next
   end while
   if n = tail