27 KiB
JavaScript algoritmlari va ma'lumotlar tuzilmalari
Bu repozitoriyada JavaScript-ga asoslangan ko'plab mashhur algoritmlar va ma'lumotlar tuzilmalarining namunalari mavjud.
Har bir algoritm va ma'lumotlar tuzilmasining alohida README fayli bo'lib, unda tegishli tushuntirishlar va qo'shimcha o'qish uchun havolalar (shu jumladan YouTube videolariga ham havolalar) mavjud.
Read this in other languages: 简体中文, 繁體中文, 한국어, 日本語, Polski, Français, Español, Português, Русский, Türkçe, Italiana, Bahasa Indonesia, Українська, Arabic, Tiếng Việt, Deutsch, Uzbek
Yodda tuting, bu loyiha faqat o'quv va tadqiqot maqsadida ishlatilishi uchun mo'ljallangan va ishlab chiqarishda ishlatilishi mumkin emas.
Ma'lumotlar tuzilmalari
Ma'lumotlar tuzilmasi - bu kompyuterda ma'lumotlarni samarali tarzda olish va o'zgartirish uchun ularni tashkil etish va saqlashning ma'lum bir usuli. Ayniqsa, ma'lumotlar tuzilmasi ma'lumot qiymatlarining to'plami, ular orasidagi munosabatlar va ma'lumotlarga qo'llanilishi mumkin bo'lgan funksiyalar yoki operatsiyalardir.
B - Boshlang'ich, A - Ilg'or
BBog'langan ro'yxatBIkki marta bog'langan ro'yxatBNavbatBStekBHash jadvaliBHeap - maksimal va minimal heap versiyalariBUstuvor navbatATrieADaraxtAIkkilik qidiruv daraxtAAVL daraxtAQizil-qora daraxtASegment daraxt - min/max/sum diapazon so'rovlari bilan misollarAFenwick daraxt (ikkilik indeksli daraxt)
AGraf (yo'naltirilgan hamda yo'naltirilmagan)AAjratilgan to'plam - union-find ma'lumotlar strukturasi yoki merge-find to'plamiABloom filtriALRU keshi - Eng kam ishlatilgan (LRU) keshi
Algoritmlar
Algoritm muammolar sinfini qanday hal qilishning aniq spetsifikatsiyasi. Bu operatsiyalar ketma-ketligini aniqlaydigan qoidalar to'plami.
B - Boshlang'ich, A - Ilg'or
Mavzu bo'yicha algoritmlar
- Matematika
BBit manipulatsiyasi - bitlarni qo'yish/olish/yangilash/tozalash, ikkilikka ko'paytirish/bo'lish, manfiy qilish va hokazo.BIkkilik suzuvchi nuqta - suzuvchi nuqtali sonlarning ikkilik tasviri.BFaktorialBFibonachchi raqam - klassik va yopiq shakldagi versiyalarBAsosiy omillar - tub omillarni topish va ularni Xardi-Ramanujan teoremasi yordamida sanashBBirlamchilik testi (sinov bo'linish usuli)BEvklid algoritmi - eng katta umumiy bo'luvchini (EKUB) hisoblashBEng kichik umumiy karrali (EKUK)BEratosfen elagi - berilgan chegaragacha barcha tub sonlarni topishBIkkining darajasimi - raqamning ikkining darajasi ekanligini tekshirish (sodda va bitli algoritmlar)BPaskal uchburchagiBKompleks sonlar - kompleks sonlar va ular bilan asosiy amallarBRadian & Daraja - radianlarni darajaga va orqaga aylantirishBTez ko'tarishBHorner metodi - polinomlarni baholashBMatritsalar - matritsalar va asosiy matritsa operatsiyalari (ko'paytirish, transpozitsiya va boshqalar).BEvklid masofasi - ikki nuqta/vektor/matritsa orasidagi masofaAButun sonlarni bo'lishAKvadrat ildiz - Nyuton metodiALiu Hui π algoritmi - N-gonlarga asoslangan π ning taxminiy hisoblariADiskret Furye transformatsiyasi - vaqt funksiyasini (signalni) uni tashkil etuvchi chastotalarga ajratish
- Sets
BKarteziya maxsuloti - bir nechta to'plamlarning ko'paytmasiBFisher–Yates Shuffle - chekli ketma-ketlikni tasodifiy almashtirishAPower Set - to'plamning barcha kichik to'plamlari (bitwise, backtracking va kaskadli echimlar)APermutatsiyalar (takroriyalash bilan va takroriyalashsiz)AKombinatsiyalar (takroriyalash bilan va takroriyalashsiz)AEng uzun umumiy ketma-ketlik (LCS)AEng uzun ortib boruvchi ketma-ketlikAEng qisqa umumiy ketma-ketlik (SCS)AKnapsack muammosi - "0/1" va "Bir-biriga bog'lanmagan"AMaksimal kichik massiv - Toʻliq kuch va dinamik dasturlash (Kadane usuli) versiyalariAKombinatsiya yig'indisi - ma'lum summani tashkil etuvchi barcha kombinatsiyalarni topish
- Stringlar
BHamming masofasi - belgilarning bir-biridan farq qiladigan pozitsiyalar soniBPalindrom - satrning teskari tomoni ham bir xil ekanligini tekshirishALevenshtein masofasi - ikki ketma-ketlik o'rtasidagi minimal tahrirlash masofasiAKnuth–Morris–Pratt Algoritmi (KMP Algoritmi) - kichik qatorlarni qidirish (mosh keluvchi naqshni qidirish)AZ Algoritmi - kichik qatorlarni qidirish (mosh keluvchi naqshni qidirish)ARabin Karp Algoritmi - kichik qatorlarni qidirishAEng uzun umumiy kichik matnARegulyar ifoda moslashuvi (RegEx)
- Qidiruvlar
BLinear qidirishBJump qidirish (yoki Blok qidirish) - saralangan qatorda qidirishBIkkilik qidirish - saralangan qatorda qidirishBInterpolatsiya qidirish - bir tekis taqsimlangan saralangan qatorda qidirish
- Tartiblash
BPufakcha tartiblashBTanlash tartibiBKiritish tartibiBHeap tartibiBBirlashtirish tartibiBTezkor saralash - joyida va joyida bo'lmagan amalga oshirishBShell tartiblashBSanash tartibiBRadiksli tartiblashBBucket tartiblash
- Bog'langan ro'yhatlar
- Daraxtlar
BBirinchi-pastga qarab qidirish (Depth-First Search)BBirinchi-yonga qarab qidirish (Breadth-First Search)
- Grafiklar
BBirinchi-pastga qarab qidirish (Depth-First Search)BBirinchi-yonga qarab qidirish (Breadth-First Search)BKruskal Algoritmi - og'irlikdagi yo'naltirilmagan grafik uchun Minimal kengayuvchi daraxtni (MST) topishADijkstra Algoritmi - grafikning bir cho'qqisidan qolgan barcha nuqtalarga eng qisqa yo'llarni topishABellman-Ford Algoritmi - grafikning bir cho'qqisidan qolgan barcha nuqtalarga eng qisqa yo'llarni topishAFloyd-Warshall Algoritmi - grafikning barcha uchlari orasidagi eng qisqa masofalarni topishASiklni aniqlash - yo'naltirilgan va yo'naltirilmagan grafiklar uchun (DFS va Disjoint Set-ga asoslangan versiyalar)APrim Algoritmi - og'irlikdagi yo'naltirilmagan grafik uchun Minimal kengayuvchi daraxtni (MST) topishATopologik saralash - DFS metodiAArtikulyatsiya nuqtalari - Tarjan algoritmi (DFS asosida)AKo'priklar - DFS asosidagi algoritmAEyler yo'li va Eyler sxemasi - Fleury algoritmi - Har bir chekkaga bir marta tashrif buyurishAGamilton sikli - Har bir cho'qqiga bir marta tashrif buyurishAKuchli bog'langan komponentlar - Kosaraju algoritmiASayohatchi sotuvchi muammosi - har bir shaharga tashrif buyuradigan va kelib chiqqan shaharga qaytib keladigan eng qisqa yo'l
- Kriptografiya
BPolynomial Hash - polinomga asoslangan hash funktsiyasiBRail Fence Cipher - xabarlarni kodlash uchun transpozitsiya shifrlash algoritmiBCaesar Cipher - oddiy almashtirish shifridirBHill Cipher - chiziqli algebraga asoslangan almashtirish shifri
- Machine Learning
BNanoNeuron - Mashinalar aslida qanday o'rganishi mumkinligini ko'rsatadigan 7 ta oddiy JS funksiyasi (forward/backward tarqalish)Bk-NN - eng yaqin qo'shnilarni tasniflash algoritmiBk-Means - k-Means kalsterlash algoritmi
- Tasvirga ishlov berish
BSeam Carving - kontentga moslashuvchan rasm o'lchamini o'zgartirish algoritmi
- Statistikalar
BWeighted Random - elementlarning og'irligi asosida ro'yxatdan tasodifiy elementni tanlash
- Evolyutsion algoritmlar
AGenetik algoritm - avtoturargohni o'rgatish uchun genetik algoritm qanday qo'llanilishiga misol.
- Kategoriyasiz
BXanoy minorasiBKvadrat matritsaning aylanishi - joyidagi algoritmBSakrash o'yini - orqaga qaytish, dinamik dasturlash (yuqoridan pastga + pastdan yuqoriga) va ochko'z misollarBNoyob yo'llar - orqaga qaytish, dinamik dasturlash va Paskal uchburchagiga asoslangan misollaBYomg'ir teraslari - yomg'ir suvini ushlab turish muammosi (dinamik dasturlash va qo'pol kuch versiyalari)BRekursiv zinapoya - yuqoriga chiqish yo'llari sonini hisoblash (4 ta echim)BAksiyalarni sotib olish va sotish uchun eng yaxshi vaqt - bo'linib-zabt etish va bir marta o'tish misollariAN-Queens MuommosiARitsar sayohati
Paradigma bo'yicha algoritmlar
Algorithmic paradigm - bu algoritmlar sinfini loyihalashtirishga asos bo'lib xizmat qiladigan umumiy usul yoki yondashuv. Bu algoritm tushunchasidan yuqori darajadagi abstraktsiya bo'lib, algoritm kompyuter dasturi tushunchasidan yuqori darajadagi abstraktsiya bo'lgani kabi.
-
Brute Force - barcha imkoniyatlarni ko'rib chiqib va eng yaxshi echimni tanlash
BChiziqli qidirishBYomg'irli teraslar - yomg'ir suvini to'plash muammosiBRekursiv zinapoya - cho'qqiga chiqish yo'llari sonini hisoblashAMaksimal kichik massivASayohatchi sotuvchi muammosi - har bir shaharga tashrif buyuradigan va kelib chiqqan shaharga qaytib keladigan eng qisqa yo'lADiskret Furye transformatsiyasi - vaqt funksiyasini (signalni) uni tashkil etuvchi chastotalarga ajratish
-
Greedy - kelajakni o'ylamasdan, hozirgi vaqtda eng yaxshi variantni tanlash
BSakrash o'yiniABog'lanmagan yukxalta muammosiADijkstra Algoritmi - grafikning bir cho'qqisidan qolgan barcha nuqtalarga eng qisqa yo'llarni topishAPrim Algoritmi - og'irlikdagi yo'naltirilmagan grafik uchun Minimal kengayuvchi daraxtni (MST) topishAKruskal Algoritmi - og'irlikdagi yo'naltirilmagan grafik uchun Minimal kengayuvchi daraxtni (MST) topish
-
Divide and Conquer - muammoni kichikroq qismlarga bo'lib va keyin bu qismlarni hal qilish
BIkkilik qidiruvBXanoy minorasiBPaskal uchburchagiBEvklid Algoritmi - eng katta umumiy bo'luvchini (EKUB) hisoblashBBirlashtirish tartibiBTezkor saralashBBirinchi-pastga qarab qidirish daraxti (DFS)BBirinchi-pastga qarab qidirish grafigi (DFS)BMatritsalar - turli shakldagi matritsalarni hosil qilish va kesib o'tishBSakrash o'yiniBTez ko'tarishBAksiyalarni sotib olish va sotish uchun eng yaxshi vaqt - bo'linib-zabt etish va bir marta o'tish misollariAPermutatsiyalar (takroriyalash bilan va takroriyalashsiz)AKombinatsiyalar (takroriyalash bilan va takroriyalashsiz)AMaksimal kichik massiv
-
Dinamik dasturlash - ilgari topilgan kichik yechimlar yordamida yechim yaratish
BFibonachchi raqamBSakrash o'yiniBNoyob yo'llarBYomg'ir teraslari - yomg'ir suvini to'plash muammosiBRecursive Staircase - count the number of ways to reach to the topBSeam Carving - kontentga moslashuvchan rasm o'lchamini o'zgartirish algoritmiALevenshtein masofasi - ikki ketma-ketlik o'rtasidagi minimal tahrirlash masofasiAEng uzun umumiy ketma-ketlik (LCS)AEng uzun umumiy kichik matnAEng uzun ortib boruvchi ketma-ketlikAEng qisqa umumiy ketma-ketlikA0/1 Knapsak muommosiAButun sonlarni bo'lishAMaksimal kichik massivABellman-Ford Algoritmi - grafikning bir cho'qqisidan qolgan barcha nuqtalarga eng qisqa yo'llarni topishAFloyd-Warshall Algoritmi -grafikning barcha uchlari orasidagi eng qisqa masofalarni topishARegulyar ifoda moslashuvi
-
Backtracking - brute forcega o'xshab, barcha mumkin bo'lgan yechimlarni generatsiya qilishga harakat qiladi, lekin har safar keyingi yechimni yaratganingizda, yechim barcha shartlarga javob beradimi yoki yo'qligini tekshirasiz va shundan keyingina keyingi yechimlarni ishlab chiqarishni davom ettirasiz. Aks holda, orqaga qaytib, yechim topishning boshqa yo'liga o'tasiz. Odatda state-space ning DFS-qidiruvi ishlatiladi.
BSakrash o'yiniBNoyob yo'llarBPower Set - to'plamning barcha kichik to'plamlariAGamilton sikli - Har bir cho'qqiga bir marta tashrif buyurishAN-Queens muommosiARitsar sayohatiAKombinatsiya yig'indisi - ma'lum summani tashkil etuvchi barcha kombinatsiyalarni topish
-
Branch & Bound - shu paytgacha topilgan eng arzon echimdan kattaroq xarajatlarga ega qisman echimlarni bekor qilish uchun, backtracking qidiruvining har bir bosqichida topilgan eng arzon echimni eslab qoling va shu paytgacha topilgan eng arzon yechim narxidan muammoni eng kam xarajatli yechim narxining past chegarasi sifatida foydalaning. Odatda state-space daraxtining DFS o'tishi bilan birgalikda BFS traversal qo'llaniladi.
Ushbu repozitoriyadan qanday foydalanish kerak
Barcha dependensiylarni o'rnating
npm install
ESLint ni ishga tushiring
Kod sifatini tekshirish uchun ESLint ni ishga tushirishingiz mumkin.
npm run lint
Barcha testlarni ishga tushuring
npm test
Testlarni nom bo'yicha ishga tushirish
npm test -- 'LinkedList'
Muammolarni bartaraf qilish (Troubleshooting)
Agar linting yoki sinov muvaffaqiyatsiz bo'lsa, node_modules papkasini o'chirib, npm paketlarini qayta o'rnatishga harakat qiling:
rm -rf ./node_modules
npm i
Shuningdek, to'g'ri Node versiyasidan foydalanayotganingizga ishonch hosil qiling (>=16). Agar Node versiyasini boshqarish uchun nvm dan foydalanayotgan bo'lsangiz, loyihaning ildiz papkasidan nvm use ni ishga tushiring va to'g'ri versiya tanlanadi.
O'yin maydoni (Playground)
./src/playground/playground.js faylida ma'lumotlar strukturalari va algoritmlar bilan o'ynashingiz, ./src/playground/test/playground.test.js faylida esa ular uchun testlar yozishingiz mumkin.
Shundan so'ng, playground kodingiz kutilgandek ishlashini tekshirish uchun quyidagi buyruqni ishga tushirishingiz kifoya:
npm test -- 'playground'
Foydali ma'lumotlar
Manbalar
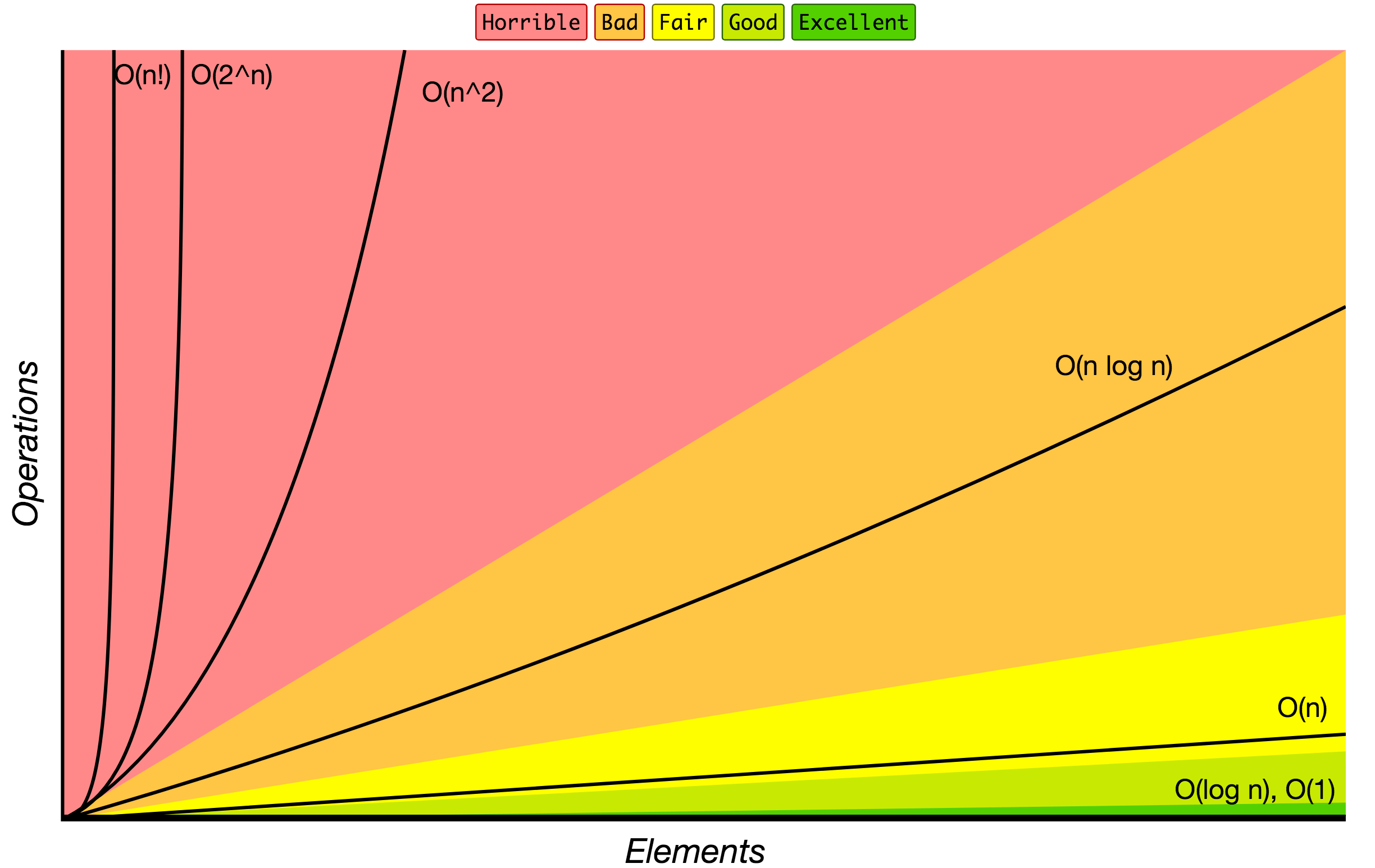
Big O Notation
Big O notation algoritmlarni kirish hajmi oshgani sayin ularning ishlash vaqti yoki bo'sh joy talablari qanday o'sishiga qarab tasniflash uchun ishlatiladi. Quyidagi jadvalda siz Big O notatsiyasida ko'rsatilgan algoritmlarning o'sishining eng keng tarqalgan tartiblarini topishingiz mumkin.
Manba: Big O Cheat Sheet.
Quyida eng ko'p qo'llaniladigan Big O notatsiyalarining ro'yxati va ularning kirish ma'lumotlarining turli o'lchamlariga nisbatan ishlashini taqqoslash keltirilgan.
| Big O Notatsiya | Turi | 10 ta element uchun hisob-kitoblar | 100 ta element uchun hisob-kitoblar | 1000 ta element uchun hisob-kitoblar |
|---|---|---|---|---|
| O(1) | O'zgarmas | 1 | 1 | 1 |
| O(log N) | Logarifmik | 3 | 6 | 9 |
| O(N) | Chiziqli | 10 | 100 | 1000 |
| O(N log N) | n log(n) | 30 | 600 | 9000 |
| O(N^2) | Kvadrat | 100 | 10000 | 1000000 |
| O(2^N) | Eksponensial | 1024 | 1.26e+29 | 1.07e+301 |
| O(N!) | Faktorial | 3628800 | 9.3e+157 | 4.02e+2567 |
Ma'lumotlar tuzilmalarining operatsiyalari murakkabligi
| Ma'lumotlar tuzilmalari | Kirish | Qidirish | Kiritish | O'chirish | Izohlar |
|---|---|---|---|---|---|
| Massiv | 1 | n | n | n | |
| Stak | n | n | 1 | 1 | |
| Navbat | n | n | 1 | 1 | |
| Bog'langan ro'yhat | n | n | 1 | n | |
| Hash jadval | - | n | n | n | Mukammal xash funksiyasi bo'lsa, xarajatlar O (1) bo'ladi. |
| Ikkilik qidiruv daraxti | n | n | n | n | Balanslangan daraxt narxida O(log(n)) bo'ladi. |
| B-daraxti | log(n) | log(n) | log(n) | log(n) | |
| Qizil-qora daraxt | log(n) | log(n) | log(n) | log(n) | |
| AVL Daraxt | log(n) | log(n) | log(n) | log(n) | |
| Bloom filtri | - | 1 | 1 | - | Qidiruv paytida noto'g'ri pozitivlar bo'lishi mumkin |
Massivlarni saralash algoritmlarining murakkabligi
| Nomi | Eng yaxshi | O'rta | Eng yomon | Xotira | Barqaror | Izohlar |
|---|---|---|---|---|---|---|
| Pufakcha tartiblash | n | n2 | n2 | 1 | Ha | |
| Kiritish tartibi | n | n2 | n2 | 1 | Ha | |
| Tanlash tartibi | n2 | n2 | n2 | 1 | Yo'q | |
| Heap tartibi | n log(n) | n log(n) | n log(n) | 1 | Yo'q | |
| Birlashtirish tartibi | n log(n) | n log(n) | n log(n) | n | Ha | |
| Tezkor saralash | n log(n) | n log(n) | n2 | log(n) | Yo'q | Tezkor saralash odatda O(log(n)) stek maydoni bilan joyida amalga oshiriladi |
| Shell tartiblash | n log(n) | depends on gap sequence | n (log(n))2 | 1 | Yo'q | |
| Sanash tartibi | n + r | n + r | n + r | n + r | Ha | r - massivdagi eng katta raqam |
| Radiksli tartiblash | n * k | n * k | n * k | n + k | Ha | k - eng uzun kalitning uzunligi |
Loyihani qo'llab-quvvatlovchilar
Siz ushbu loyihani ❤️️ GitHub yoki ❤️️ Patreon orqali qo'llab-quvvatlashingiz mumkin.
Ushbu loyihani qo'llab-quvvatlagan odamlar ∑ = 1
Muallif
A few more projects and articles about JavaScript and algorithms on trekhleb.dev