javascript-algorithms/README.zh-CN.md

JavaScript 算法与数据结构

本仓库包含了多种基于 JavaScript 的算法与数据结构。

每种算法和数据结构都有自己的 README 并提供相关说明以及进一步阅读和 YouTube 视频。

Read this in other languages: English, 繁體中文, 한국어, Polski, Français, Español

We’re writing a book that will clearly explain, in detail, the main algorithms. If you’d like to be notified when the “JavaScript Algorithms” book launches, click here.

数据结构

数据结构是在计算机中 组织和存储数 据的一种特殊方式, 它可以高效地 访问和修改 数据。更确切地说, 数据结构是数据值的集合, 它们之间的关系、函数或操作可以应用于数据。

B - 初学者, A - 进阶

• B 链表
• B 双向链表
• B 队列
• B 栈
• B 哈希表
• B 堆
• B 优先队列
• A 字典树
• A 树
  • A 二叉查找树
  • A AVL 树
  • A 红黑树
  • A 线段树 - 使用 最小/最大/总和 范围查询示例
  • A 树状数组 (二叉索引树)
• A 图 (有向图与无向图)
• A 并查集
• A 布隆过滤器

算法

算法是如何解决一类问题的明确规范。 算法是一组精确定义操作序列的规则。

算法主题

• 数学
• B Bit 操控 - set/get/update/clear 位, 乘以/除以 二进制位, 变负 等.
• B 阶乘
• B 斐波那契数
• B 素数检测 (排除法)
• B 欧几里得算法 - 计算最大公约数 (GCD)
• B 最小公倍数 (LCM)
• B 素数筛 - 查找所有素数达到任何给定限制
• B 判断2次方数 - 检查数字是否为2的幂 (原生和按位算法)
• B 杨辉三角形
• A 整数拆分
• A 割圆术 - 基于N-gons的近似π计算
• 集合
  • B 笛卡尔积 - 多集合结果
  • A 幂集 - 该集合的所有子集
  • A 排列 (有/无重复)
  • A 组合 (有/无重复)
  • A 洗牌算法 - 随机置换有限序列
  • A 最长公共子序列 (LCS)
  • A 最长递增子序列
  • A 最短公共父序列 (SCS)
  • A 背包问题 - "0/1" and "Unbound" ones
  • A 最大子数列问题 - BF算法 与 动态规划
  • A 组合求和 - 查找形成特定总和的所有组合
• 字符串
  • A 莱温斯坦距离 - 两个序列之间的最小编辑距离
  • B 汉明距离 - 符号不同的位置数
  • A 克努斯-莫里斯-普拉特算法 - 子串搜索
  • A 字符串快速查找 - 子串搜索
  • A 最长公共子串
  • A 正则表达式匹配
• 搜索
  • B 线性搜索
  • B 跳转搜索 (或块搜索) - 搜索排序数组
  • B 二分查找
  • B 插值搜索 - 搜索均匀分布的排序数组
• 排序
  • B 冒泡排序
  • B 选择排序
  • B 插入排序
  • B 堆排序
  • B 归并排序
  • B 快速排序
  • B 希尔排序
  • B 计数排序
  • B 基数排序
• 树
  • B 深度优先搜索 (DFS)
  • B 广度优先搜索 (BFS)
• 图
  • B 深度优先搜索 (DFS)
  • B 广度优先搜索 (BFS)
  • A 戴克斯特拉算法 - 找到图中所有顶点的最短路径
  • A 贝尔曼-福特算法 - 找到图中所有顶点的最短路径
  • A 弗洛伊德算法 - 找到所有顶点对 之间的最短路径
  • A 判圈算法 - 对于有向图和无向图 (基于DFS和不相交集的版本)
  • A 普林演算法 - 寻找加权无向图的最小生成树 (MST)
  • B 克鲁斯克尔演算法 - 寻找加权无向图的最小生成树 (MST)
  • A 拓扑排序 - DFS 方法
  • A 关节点 - Tarjan算法 (基于DFS)
  • A 桥 - 基于DFS的算法
  • A 欧拉回径与一笔画问题 - Fleury的算法 - 一次访问每个边
  • A 哈密顿图 - 恰好访问每个顶点一次
  • A 强连通分量 - Kosaraju算法
  • A 旅行推销员问题 - 尽可能以最短的路线访问每个城市并返回原始城市
• 未分类
  • B 汉诺塔
  • B 旋转矩阵 - 原地算法
  • B 跳跃 游戏 - 回溯, 动态编程 (自上而下+自下而上) 和贪婪的例子
  • B 独特(唯一) 路径 - 回溯, 动态编程和基于Pascal三角形的例子
  • B 雨水收集 - 诱捕雨水问题 (动态编程和暴力版本)
  • A 八皇后问题
  • A 骑士巡逻

算法范式

算法范式是基于类的设计的通用方法或方法的算法。 这是一个比算法概念更高的抽象, 就像一个 算法是比计算机程序更高的抽象。

• BF算法 - 查找/搜索 所有可能性并选择最佳解决方案

  • B 线性搜索
  • B 雨水收集 - 诱导雨水问题
  • A 最大子数列
  • A 旅行推销员问题 - 尽可能以最短的路线访问每个城市并返回原始城市

• 贪心法 - 在当前选择最佳选项, 不考虑以后情况

  • B 跳跃游戏
  • A 背包问题
  • A 戴克斯特拉算法 - 找到所有图顶点的最短路径
  • A 普里姆算法 - 寻找加权无向图的最小生成树 (MST)
  • A 克鲁斯卡尔算法 - 寻找加权无向图的最小生成树 (MST)

• 分治法 - 将问题分成较小的部分, 然后解决这些部分

  • B 二分查找
  • B 汉诺塔
  • B 杨辉三角形
  • B 欧几里得算法 - 计算最大公约数 (GCD)
  • B 跳跃游戏
  • B 归并排序
  • B 快速排序
  • B 树深度优先搜索 (DFS)
  • B 图深度优先搜索 (DFS)
  • A 排列 (有/无重复)
  • A 组合 (有/无重复)

• 动态编程 - 使用以前找到的子解决方案构建解决方案

• B 斐波那契数

• B 跳跃游戏

• B 独特路径

• B 雨水收集 - 疏导雨水问题

• A 莱温斯坦距离 - 两个序列之间的最小编辑距离

• A 最长公共子序列 (LCS)

• A 最长公共子串

• A 最长递增子序列

• A 最短公共子序列

• A 0-1背包问题

• A 整数拆分

• A 最大子数列

• A 弗洛伊德算法 - 找到所有顶点对之间的最短路径

• A 贝尔曼-福特算法 - 找到所有图顶点的最短路径

• 回溯法 - 类似于 BF算法 试图产生所有可能的解决方案, 但每次生成解决方案测试如果它满足所有条件, 那么只有继续生成后续解决方案。 否则回溯并继续寻找不同路径的解决方案。

  • B 跳跃游戏
  • B 独特路径
  • A 哈密顿图 - 恰好访问每个顶点一次
  • A 八皇后问题
  • A 骑士巡逻
  • A 组合求和 - 从规定的总和中找出所有的组合

• Branch & Bound

如何使用本仓库

安装依赖

npm install

执行测试

npm test

按照名称执行测试

npm test -- 'LinkedList'

Playground

你可以在./src/playground/playground.js文件中操作数据结构与算法, 并在./src/playground/__test__/playground.test.js中编写测试。

然后, 只需运行以下命令来测试你的 Playground 是否按无误:

npm test -- 'playground'

有用的信息

引用

▶ YouTube

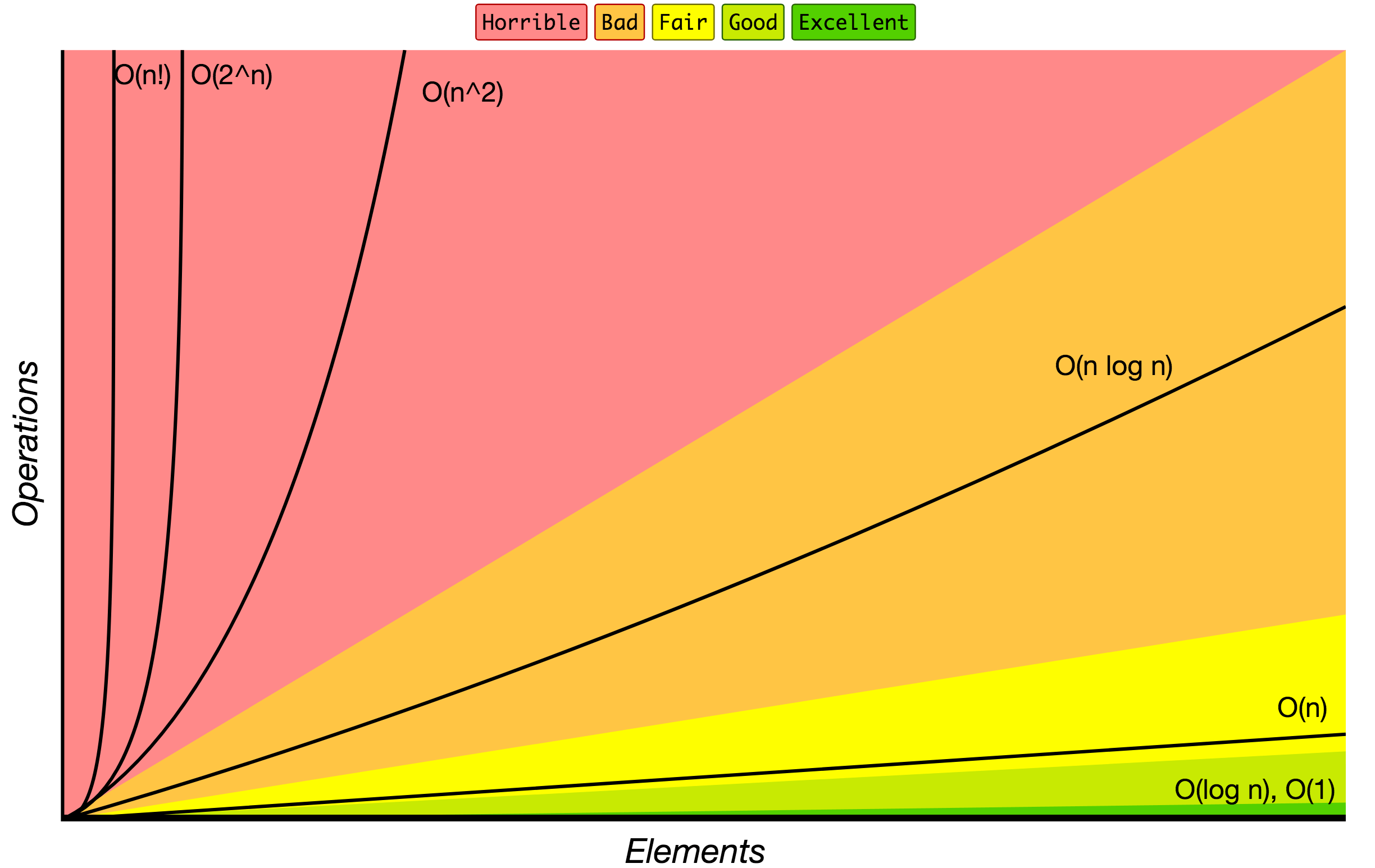
大O符号

大O符号中指定的算法的增长顺序。

源: Big O Cheat Sheet.

以下是一些最常用的 大O标记法 列表以及它们与不同大小输入数据的性能比较。

大O标记法	计算10个元素	计算100个元素	计算1000个元素
O(1)	1	1	1
O(log N)	3	6	9
O(N)	10	100	1000
O(N log N)	30	600	9000
O(N^2)	100	10000	1000000
O(2^N)	1024	1.26e+29	1.07e+301
O(N!)	3628800	9.3e+157	4.02e+2567

数据结构操作的复杂性

数据结构	连接	查找	插入	删除
数组	1	n	n	n
栈	n	n	1	1
队列	n	n	1	1
链表	n	n	1	1
哈希表	-	n	n	n
二分查找树	n	n	n	n
B树	log(n)	log(n)	log(n)	log(n)
红黑树	log(n)	log(n)	log(n)	log(n)
AVL树	log(n)	log(n)	log(n)	log(n)

数组排序算法的复杂性

名称	最优	平均	最坏	内存	稳定
冒泡排序	n	n^2	n^2	1	Yes
插入排序	n	n^2	n^2	1	Yes
选择排序	n^2	n^2	n^2	1	No
堆排序	n log(n)	n log(n)	n log(n)	1	No
归并排序	n log(n)	n log(n)	n log(n)	n	Yes
快速排序	n log(n)	n log(n)	n^2	log(n)	No
希尔排序	n log(n)	取决于差距序列	n (log(n))^2	1	No