hxx/javascript-algorithms

Fork 0

mirror of https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git synced 2024-11-10 11:09:43 +08:00

Deniz Binay 64abcf12f2

add german translation for main readme (#703 )

2021-05-06 06:46:04 +02:00

24 KiB

Raw Blame History

Algoritme dan Struktur Data Javascript

Repositori ini berisi contoh-contoh algoritme dan struktur data yang populer menggunakan JavaScript.

Setiap algoritme dan struktur data memiliki README-nya tersendiri dengan penjelasan yang berkaitan dan tautan untuk bacaan lebih lanjut (termasuk tautan menuju video YouTube).

Baca ini dalam bahasa yang lain: English, 简体中文, 繁體中文, 한국어, 日本語, Polski, Français, Español, Português, Русский, Türk, Italiana, Українська, Arabic, Deutsch

☝ Perhatikan bahwa proyek ini hanya dimaksudkan untuk tujuan pembelajaran dan riset, dan tidak dimaksudkan untuk digunakan sebagai produksi.

Struktur Data

Struktur data adalah cara tertentu untuk mengatur dan menyimpan data dalam komputer sehingga dapat diakses dan diubah secara efisien. Lebih tepatnya, struktur data adalah kumpulan dari nilai data, relasi di antara data-data, dan fungsi atau operasi yang dapat diterapkan pada data.

P - Pemula, L - Lanjutan

P Senarai Berantai
P Senarai Berantai Ganda
P Antrean
P Tumpukan
P Tabel Hash
P Heap - versi heap maksimum dan minimum
P Antrean Prioritas
L Trie
L Pohon
- L Pohon Telusur Biner
- L AVL Tree
- L Pohon Merah Hitam
- L Segment Tree - dengan contoh min/max/sum range query
- L Pohon Fenwick (Binary Indexed Tree)
L Graf (directed dan undirected)
L Disjoint Set
L Bloom Filter

Algoritme

Algoritme adalah sebuah perincian yang jelas tentang cara untuk memecahkan suatu masalah. Ia adalah sekumpulan aturan yang menjelaskan secara tepat urutan-urutan dari sebuah operasi.

P - Pemula, L - Lanjutan

Algoritme Berdasarkanan Topik

Matematika
- P Manipulasi Bit - menetapkan/mendapatkan/memperbarui/mengahpus bit, perkalian/pembagian dengan angka 2, membuat bilangan negatif etc.
- P Faktorial
- P Bilangan Fibonacci - versi klasik dan bentuk tertutup
- P Faktor Prima - menemukan faktor prima dan menghitungnya menggunakan teorema Hardy-Ramanujan
- P Pengujian Bilangan Prima (metode trial division)
- P Algoritme Euclidean - menghitung Faktor Persekutuan Terbesar (FPB)
- P Least Common Multiple (LCM)
- P Sieve of Eratosthenes - menemukan semua bilangan prima hingga batas yang ditentukan
- P Is Power of Two - mengecek apakah sebuah bilangan adalah hasil dari pangkat dua (algoritme naive dan bitwise)
- P Segitiga Pascal
- P Bilangan Kompleks - bilangan kompleks dengan operasi dasarnya
- P Radian & Derajat - konversi radian ke derajat dan sebaliknya
- P Fast Powering
- P Metode Horner - evaluasi polinomial
- L Partisi Bilangan Bulat
- L Akar Pangkat Dua - metode Newton
- L Algoritme π Liu Hui - perkiraan perhitungan π berdasarkan segibanyak
- L Transformasi Diskrit Fourier - menguraikan fungsi waktu (sinyal) menjadi frekuensi yang menyusunnya
Himpunan
- P Produk Kartesian - hasil dari beberapa himpunan
- P Pengocokan Fisher–Yates - permutasi acak dari sebuah urutan terhingga
- L Himpunan Kuasa - semua himpunan bagian dari sebuah himpunan
- L Permutasi (dengan dan tanpa pengulangan)
- L Kombinasi (dengan dan tanpa pengulangan)
- L Longest Common Subsequence (LCS)
- L Longest Increasing Subsequence
- L Shortest Common Supersequence (SCS)
- L Permasalahan Knapsack - "0/1" dan yang tidak "dibatasi"
- L Upalarik Maksimum - "Brute Force" dan "Pemrograman Dinamis" versi Kadane
- L Combination Sum - menemukan semua kombinasi yang membentuk jumlah tertentu
String
- P Jarak Hamming - jumlah posisi di mana ditemukan simbol-simbol yang berbeda
- L Algoritme Jarak Levenshtein - edit distance minimum antara dua urutan
- L Algoritme Knuth–Morris–Pratt (Algoritme KMP) - pencarian substring (pencocokan pola)
- L AlgoritmeZ - pencarian substring (pencocokan pola)
- L Algoritme Rabin Karp - pencarian substring
- L Longest Common Substring
- L Pencocokan Ekspresi Reguler
Pencarian
- P Pencarian Linier
- P Pencarian Lompat (atau Block Search) - pencarian di larik tersortir
- P Pencarian Biner - pencarian di larik tersortir
- P Pencarian Interpolasi - pencarian di larik tersortir yang terdistribusi seragam
Penyortiran
- P Sortir Gelembung
- P Sortir Seleksi
- P Sortir Sisipan
- P Sortir Heap
- P Sortir Gabungan
- P Sortir Cepat - implementasi in-place dan non-in-place
- P Sortir Shell
- P Sortir Perhitungan
- P Sortir Akar
Senarai Berantai
- P Lintas Lurus
- P Lintas Terbalik
Pohon
- P Pencarian Kedalaman Pertama (DFS)
- P Pencarian Luas Pertama (BFS)
Graf
- P Pencarian Kedalaman Pertama (DFS)
- P Pencarian Luas Pertama (BFS)
- P Algoritme Kruskal - mencari rentang pohon minimum untuk graf tidak berarah berbobot
- L Algoritme Dijkstra - menemukan jalur terpendek ke semua sudut graf dari sudut tunggal
- L Algoritme Bellman-Ford - menemukan jalur terpendek ke semua sudut graf dari sudut tunggal
- L Algoritme Floyd-Warshall - menemukan jalur terpendek antara semua pasangan sudut
- L Mendeteksi Siklus - untuk graf berarah dan tidak berarah (berdasarkan versi DFS dan Disjoint Set)
- L ALgoritme Prim - mencari rentang pohon minimum untuk graf tidak berarah berbobot
- L Sortir Topologi - metode DFS
- L Poin Artikulasi - Algoritme Tarjan (berdasarkan DFS)
- L Jembatan - Algoritme berdasarkan DFS
- L Jalur dan Sirkuit Eulerian - Algoritme Fleury - Mengunjungi setiap tepinya tepat satu kali
- L Siklus Hamiltonian - mengunjungi setiap sudutnya tepat satu kali
- L Komponen yang Terkoneksi dengan Kuat - Algoritme Kosaraju
- L Permasalahan Penjual Keliling - kemungkinan rute terpendek untuk mengunjungi setiap kota dan kembali lagi ke kota asal
Kriptografi
- P Polinomial Hash - fungsi rolling hash berdasarkan polinomial
- P Sandi Caesar - sandi pengganti sederhana
Pembelajaran Mesin
- P NanoNeuron - 7 fungsi JS sederhana yang mengilustrasikan bagaimana mesin-mesin dapat benar-benar belajar (perambatan maju/mundur)
Tidak Dikategorikan
- P Menara Hanoi
- P Perputaran Matriks Persegi - algoritme in-place
- P Permainan Melompat - runut-balik, pemrograman dinamis (atas ke bawah + bawah ke atas) and contoh-contoh greedy
- P Unique Paths - runut-balik, pemrograman dinamis and contoh-contoh beradsarkan Segitiga Pascal
- P Rain Terraces - permasalahan trapping rain water (versi pemrograman dinamis and brute force)
- P Tangga Rekursif - menghitung jumlah cara untuk mencapai ke atas tangga (4 solusi)
- L Permainan N-Queen
- L Permainan Knight's Tour

Algoritme Berdasarkan Paradigma

Paradigma algoritmik adalah sebuah metode atau pendekatan umum yang mendasari desain sebuah tingkatan algoritme. Paradigma algoritmik merupakan abstraksi yang lebih tinggi dari gagasan sebuah algoritme, seperti halnya sebuah algoritme merupakan abstraksi yang lebih tinggi dari sebuah program komputer.

Brute Force - melihat ke semua kemungkinan dan memilih solusi yang terbaik
- P Pencarian Linier
- P Rain Terraces - permasalahan trapping rain water
- P Tangga Rekursif - menghitung jumlah cara untuk mencapai ke atas tangga
- L Upalarik Maksimum
- L Permasalahan Penjual Keliling - kemungkinan rute terpendek untuk mengunjungi setiap kota dan kembali lagi ke kota asal
- L Transformasi Diskrit Fourier - menguraikan fungsi waktu (sinyal) menjadi frekuensi yang menyusunnya
Greedy - memilih pilihan terbaik pada saat ini tanpa mempertimbangkan masa yang akan datang
- P Permainan Melompat
- L Permasalahan Knapsack yang Tidak Dibatasi
- L Algoritme Dijkstra - menemukan jalur terpendek ke semua sudut graf dari sudut tunggal
- L Algoritme Prim - mencari rentang pohon minimum untuk graf tidak berarah berbobot
- L Algoritme Kruskal - mencari rentang pohon minimum untuk graf tidak berarah berbobot
Memecah dan Menaklukkan - membagi masalah menjadi bagian-bagian yang kecil, lalu memcahkan bagian-bagian tersebut
- P Pencarian Biner
- P Menara Hanoi
- P Segitiga Pascal
- P Algoritme Euclidean - menghitung Faktor Persekutuan Terbesar (FPB)
- P Sortir Gabungan
- P Sortir Cepat
- P Pencarian Kedalaman Pertama untuk Pohon (DFS)
- P Pencarian Kedalaman Pertama untuk Graf (DFS)
- P Permainan Melompat
- P Fast Powering
- L Permutasi (dengan dan tanpa pengulangan)
- L Kombinasi (dengan dan tanpa pengulangan)
Pemrograman Dinamis - membangun sebuah solusi menggunakan upasolusi yang ditemukan sebelumnya
- P Bilangan Fibonacci
- P Permainan Melompat
- P Unique Paths
- P Rain Terraces - permasalahan trapping rain water
- P Tangga Rekursif - menghitung jumlah cara untuk mencapai ke atas tangga
- L Algoritme Jarak Levenshtein - edit distance minimum antara dua urutan
- L Longest Common Subsquence (LCS)
- L Longest Common Substring
- L Longest Increasing Subsequence
- L Shortest Common Supersequence
- L Permasalahan Knapsack 0/1
- L Partisi Bilangan Bulat
- L Upalarik Maksimum
- L Algoritme Bellman-Ford - menemukan jalur terpendek ke semua sudut graf dari sudut tunggal
- L Algoritme Floyd-Warshall - menemukan jalur terpendek antara semua pasangan sudut
- L Pencocokan Ekspresi Reguler
Runut-balik - sama halnya dengan brute force, algoritme ini mencoba untuk menghasilkan segala kemungkinan solusi, tetapi setiap kali anda menghasilkan solusi selanjutnya, anda akan menguji apakah solusi tersebut memenuhi semua kondisi dan setelah itu baru akan menghasilkan solusi berikutnya. Apabila tidak, maka akan merunut-balik dan mencari solusi di jalur yang berbeda. Biasanya menggunakan lintas DFS dari ruang keadaan.
- P Permainan Melompat
- P Unique Paths
- P Himpunan Kuasa - semua himpunan bagian dari sebuah himpunan
- L Siklus Hamiltonian - mengunjungi setiap sudutnya tepat satu kali
- L Permainan N-Queen
- L Permainan Knight's Tour
- L Combination Sum - menemukan semua kombinasi yang membentuk jumlah tertentu
Mencabang dan Membatasi - digunakan untuk membuang solusi parsial dengan biaya yang lebih besar dari solusi dengan biaya yang terendah yang ditemukan sejauh ini dengan cara mengingat solusi dengan biaya terendah yang ditemukan pada setiap tahap dari pencarian runut-balik dan menggunakan biaya dari solusi dengan biaya terendah sejauh ini sebagai batas bawah pada biaya dari solusi dengan biaya yang paling sedikit untuk permasalahannya. Biasanya menggunakan lintas BFS yang berkombinasi dengan lintas DFS dari pohon ruang keadaan.

Cara menggunakan repositori ini

Meng-install semua dependensi

npm install

Menjalankan ESLint

Anda dapat menjalankannya untuk memeriksa kualitas kode.

npm run lint

Menjalankan semua tes

npm test

Menjalankan tes berdasarkan nama

npm test -- 'LinkedList'

Playground

Anda dapat bermain dengan algoritme dan struktur data di file ./src/playground/playground.js dan menuliskan tesnya di ./src/playground/__test__/playground.test.js.

Lalu, hanya tinggal menjalankan perintah berikut untuk mengetes apakah kode playground anda bekerja sesuai dengan keinginan:

npm test -- 'playground'

Informasi Bermanfaat

Referensi

▶ Algoritme dan Struktur Data di YouTube

Notasi Big O

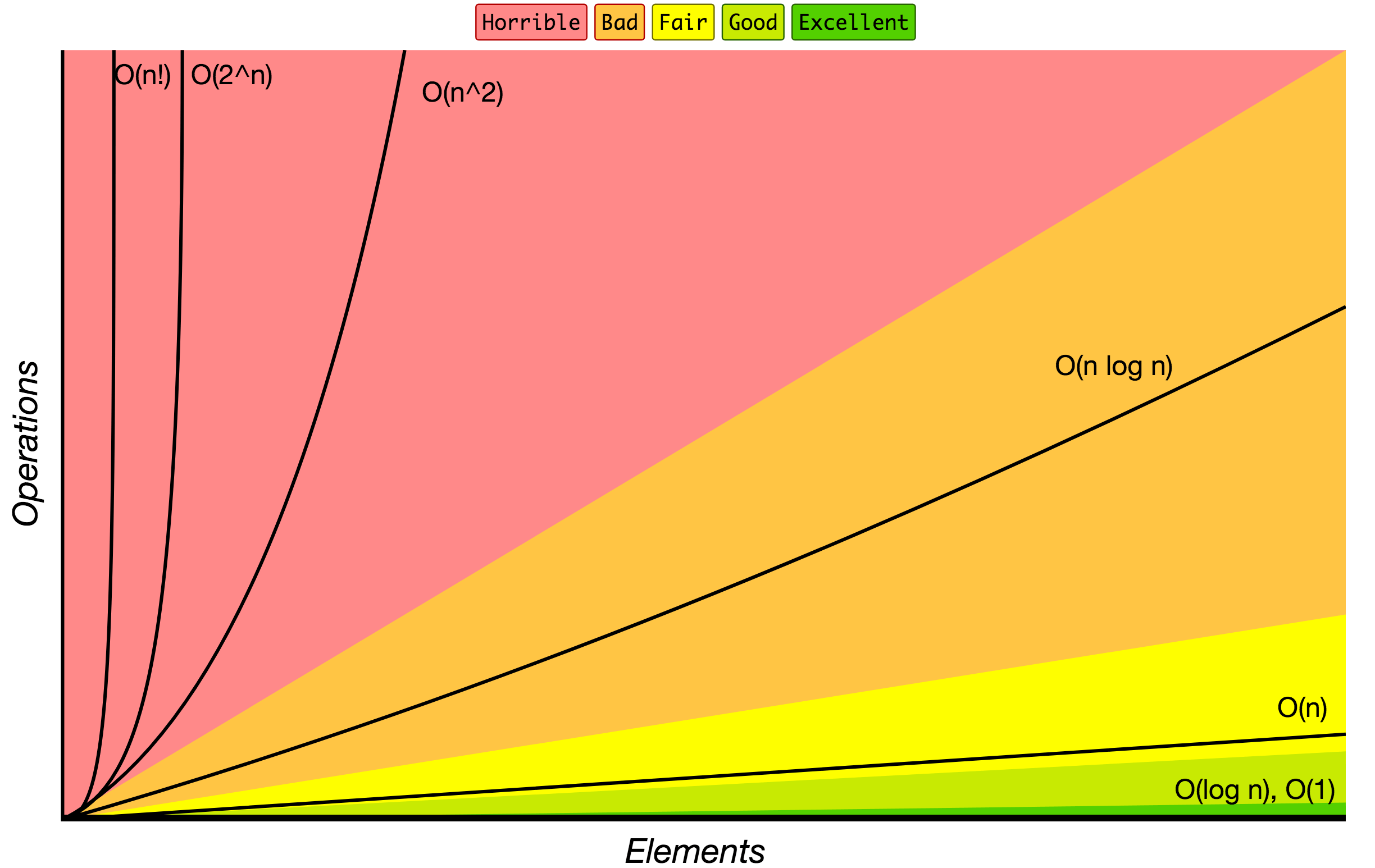
Notasi Big O digunakan untuk mengklasifikasikan algoritme berdasarkan durasi atau ruang yang dibutuhkan seiring bertambahnya input. Pada grafik dibawah, anda dapat menemukan urutan pertumbuhan yang paling umum dari algoritme yang ditentukan dalam notasi Big O.

Sumber: Big O Cheat Sheet.

Di bawah ini adalah daftar dari beberapa notasi Bog O yang sering digunakan dan perbandingan kinerjanya terhadap berbagai ukuran input data.

Notasi Big O	Komputasi untuk 10 elemen	Komputasi untuk 100 elemen	Komputasi untuk 1000 elemen
O(1)	1	1	1
O(log N)	3	6	9
O(N)	10	100	1000
O(N log N)	30	600	9000
O(N^2)	100	10000	1000000
O(2^N)	1024	1.26e+29	1.07e+301
O(N!)	3628800	9.3e+157	4.02e+2567

Kompleksitas Operasi Struktur Data

Struktur Data	Akses	Pencarian	Penyisipan	Penghapusan	Keterangan
Array (Larik)	1	n	n	n
Stack (Tumpukan)	n	n	1	1
Queue (Antrean)	n	n	1	1
Linked List (Senarai Berantai)	n	n	1	n
Hash Table	-	n	n	n	Apabila fungsi hash sempurna, biayanya akan menjadi O(1)
Binary Search Tree (Pohon Telusur Biner)	n	n	n	n	Apabila pohon seimbang, biayanya akan menjadi O(log(n))
B-Tree	log(n)	log(n)	log(n)	log(n)
Red-Black Tree (Pohon Merah-Hitam)	log(n)	log(n)	log(n)	log(n)
AVL Tree	log(n)	log(n)	log(n)	log(n)
Bloom Filter	-	1	1	-	Positif palsu dimungkinkan saat pencarian

Kompleksitas Algoritme Sortir Larik

Nama	Terbaik	Rata-rata	Terburuk	Memori	Stabil	Keterangan
Bubble sort (Sortir Gelembung)	n	n²	n²	1	Ya
Insertion sort (Sortir Sisipan)	n	n²	n²	1	Ya
Selection sort (Sortir Seleksi)	n²	n²	n²	1	Tidak
*Heap sort (Sortir Heap)*	n log(n)	n log(n)	n log(n)	1	Tidak
Merge Sort (Sortir Gabungan)	n log(n)	n log(n)	n log(n)	n	Ya
Quick sort (Sortir Cepat)	n log(n)	n log(n)	n²	log(n)	Tidak	Sortir Cepat biasanya dilakukan secara in-place dengan O(log(n)) ruang tumpukan
Shell sort (Sortir Shell)	n log(n)	tergantung pada jarak urutan	n (log(n))²	1	Tidak
Counting sort (Sortir Perhitungan)	n + r	n + r	n + r	n + r	Ya	r - angka terbesar dalam larik
Radix sort (Sortir Akar)	n * k	n * k	n * k	n + k	Ya	k - panjang dari kunci terpanjang

Pendukung Proyek

Anda dapat mendukung proyek ini via ❤️️ GitHub atau ❤️️ Patreon.

Orang-orang yang mendukung proyek ini ∑ = 1

24 KiB Raw Blame History Unescape Escape