javascript-algorithms/README.ru-RU.md

Алгоритмы и структуры данных на JavaScript

В этом репозитории содержатся базовые JavaScript-примеры многих популярных алгоритмов и структур данных.

Для каждого алгоритма и структуры данных есть свой файл README с соответствующими пояснениями и ссылками на материалы для дальнейшего изучения (в том числе и ссылки на видеоролики в YouTube).

Читать на других языках: English, 简体中文, 繁體中文, 한국어, 日本語, Polski, Français, Español, Português, Türk, Italiana, Bahasa Indonesia, Українська, Arabic

☝ Замечание: этот репозиторий предназначен для учебно-исследовательских целей (не для использования в продакшн-системах).

Структуры данных

Структура данных (англ. data structure) — программная единица, позволяющая хранить и обрабатывать множество однотипных и/или логически связанных данных в вычислительной технике. Для добавления, поиска, изменения и удаления данных структура данных предоставляет некоторый набор функций, составляющих её интерфейс.

B - Базовый уровень, A - Продвинутый уровень

• B Связный список
• B Двунаправленный связный список
• B Очередь
• B Стек
• B Хеш-табица
• B Куча — максимальная и минимальная версии
• B Очередь с приоритетом
• A Префиксное дерево
• A Деревья
  • A Двоичное дерево поиска
  • A АВЛ-дерево
  • A Красно-чёрное дерево
  • A Дерево отрезков — для минимума, максимума и суммы отрезков
  • A Дерево Фенвика (двоичное индексированное дерево)
• A Граф (ориентированный и неориентированный)
• A Система непересекающихся множеств
• A Фильтр Блума

Алгоритмы

Алгоритм — конечная совокупность точно заданных правил решения некоторого класса задач или набор инструкций, описывающих порядок действий исполнителя для решения некоторой задачи.

B - Базовый уровень, A - Продвинутый уровень

Алгоритмы по тематике

• Математика
  • B Битовые манипуляции — получение/запись/сброс/обновление битов, умножение/деление на 2, сделать отрицательным и т.п.
  • B Факториал
  • B Числа Фибоначчи — классическое решение, решение в замкнутой форме
  • B Тест простоты (метод пробного деления)
  • B Алгоритм Евклида — нахождение наибольшего общего делителя (НОД)
  • B Наименьшее общее кратное (НОК)
  • B Решето Эратосфена — нахождение всех простых чисел до некоторого целого числа n
  • B Степень двойки — является ли число степенью двойки (простое и побитовое решения)
  • B Треугольник Паскаля
  • B Комплексные числа — комплексные числа, базовые операции над ними
  • B Радианы и градусы — конвертирование радианов в градусы и наоборот
  • B Быстрое возведение в степень
  • A Разбиение числа
  • A Квадратный корень — метод Ньютона
  • A Алгоритм Лю Хуэя — расчёт числа π с заданной точностью методом вписанных правильных многоугольников
  • A Дискретное преобразование Фурье — разложение временной функции (сигнала) на частотные составляющие
• Множества
  • B Декартово произведение — результат перемножения множеств
  • B Тасование Фишера — Йетса — создание случайных перестановок конечного множества
  • A Булеан — все подмножества заданного множества (побитовый поиск и поиск с возвратом)
  • A Перестановки (с повторениями и без повторений)
  • A Сочетания (с повторениями и без повторений)
  • A Наибольшая общая подпоследовательность
  • A Наибольшая увеличивающаяся подпоследовательность
  • A Наименьшая общая супер-последовательность
  • A Задача о рюкзаке — "0/1" и "неограниченный" рюкзаки
  • A Максимальный под-массив — метод полного перебора и алгоритм Кадане
  • A Комбинации сумм — нахождение всех комбинаций, сумма каждой из которых равна заданному числу
• Алгоритмы работы со строками
  • B Расстояние Хэмминга — число позиций, в которых соответствующие символы различны
  • A Расстояние Левенштейна — метрика, измеряющая разность между двумя последовательностями
  • A Алгоритм Кнута — Морриса — Пратта — поиск подстроки (сопоставление с шаблоном)
  • A Z-функция — поиск подстроки (сопоставление с шаблоном)
  • A Алгоритм Рабина — Карпа — поиск подстроки
  • A Наибольшая общая подстрока
  • A Разборщик регулярных выражений
• Алгоритмы поиска
  • B Линейный поиск
  • B Поиск с перескоком (поиск блоков) — поиск в упорядоченном массиве
  • B Двоичный поиск — поиск в упорядоченном массиве
  • B Интерполяционный поиск — поиск в равномерно распределённом упорядоченном массиве.
• Алгоритмы сортировки
  • B Сортировка пузырьком
  • B Сортировка выбором
  • B Сортировка вставками
  • B Пирамидальная сортировка (сортировка кучей)
  • B Сортировка слиянием
  • B Быстрая сортировка — с использованием дополнительной памяти и без её использования
  • B Сортировка Шелла
  • B Сортировка подсчётом
  • B Поразрядная сортировка
• Связный список
  • B Прямой обход
  • B Обратный обход
• Деревья
  • B Поиск в глубину
  • B Поиск в ширину
• Графы
  • B Поиск в глубину
  • B Поиск в ширину
  • B Алгоритм Краскала — нахождение минимального остовного дерева для взвешенного неориентированного графа
  • A Алгоритм Дейкстры — нахождение кратчайших путей от одной из вершин графа до всех остальных
  • A Алгоритм Беллмана — Форда — нахождение кратчайших путей от одной из вершин графа до всех остальных
  • A Алгоритм Флойда — Уоршелла — нахождение кратчайших расстояний между всеми вершинами графа
  • A Задача нахождения цикла — для ориентированных и неориентированных графов (на основе поиска в глубину и системы непересекающихся множеств)
  • A Алгоритм Прима — нахождение минимального остовного дерева для взвешенного неориентированного графа
  • A Топологическая сортировка — на основе поиска в глубину
  • A Шарниры (разделяющие вершины) — алгоритм Тарьяна (на основе поиска в глубину)
  • A Мосты — на основе поиска в глубину
  • A Эйлеров путь и Эйлеров цикл — алгоритм Флёри (однократное посещение каждой вершины)
  • A Гамильтонов цикл — проходит через каждую вершину графа ровно один раз
  • A Компоненты сильной связности — алгоритм Косарайю
  • A Задача коммивояжёра — кратчайший маршрут, проходящий через указанные города с последующим возвратом в исходный город
• Криптография
  • B Полиноминальный хэш — функция кольцевого хэша, основанная на полиноме
• Машинное обучение
  • B Нано-нейрон — 7 простых JavaScript функций, отображающих способности машины к обучению (прямое и обратное распространение)
• Прочие алгоритмы
  • B Ханойская башня
  • B Поворот квадратной матрицы — используется дополнительная память
  • B Прыжки — на основе бэктрекинга, динамического программирования (сверху-вниз + снизу-вверх) и жадных алгоритмов
  • B Поиск уникальных путей — на основе бэктрекинга, динамического программирования и треугольника Паскаля
  • B Подсчёт дождевой воды — на основе перебора и динамического программирования
  • B Задача о рекурсивной лестнице — подсчёт количества путей, по которым можно достичь верха лестницы (4 способа)
  • A Задача об N ферзях
  • A Маршрут коня

Алгоритмы по парадигме программирования

Парадигма программирования — общий метод или подход, лежащий в основе целого класса алгоритмов. Понятие "парадигма программирования" является более абстрактным по отношению к понятию "алгоритм", которое в свою очередь является более абстрактным по отношению к понятию "компьютерная программа".

• Алгоритмы полного перебора — поиск лучшего решения исчерпыванием всевозможных вариантов
  • B Линейный поиск
  • B Подсчёт дождевой воды
  • B Задача о рекурсивной лестнице — подсчёт количества путей, по которым можно достичь верха лестницы
  • A Максимальный подмассив
  • A Задача коммивояжёра — кратчайший маршрут, проходящий через указанные города с последующим возвратом в исходный город
  • A Дискретное преобразование Фурье — разложение временной функции (сигнала) на частотные составляющие
• Жадные алгоритмы — принятие локально оптимальных решений с учётом допущения об оптимальности конечного решения
  • B Прыжки
  • A Задача о неограниченном рюкзаке
  • A Алгоритм Дейкстры — нахождение кратчайших путей от одной из вершин графа до всех остальных
  • A Алгоритм Прима — нахождение минимального остовного дерева для взвешенного неориентированного графа
  • A Алгоритм Краскала — нахождение минимального остовного дерева для взвешенного неориентированного графа
• Разделяй и властвуй — рекурсивное разбиение решаемой задачи на более мелкие
  • B Двоичный поиск
  • B Ханойская башня
  • B Треугольник Паскаля
  • B Алгоритм Евклида — нахождение наибольшего общего делителя (НОД)
  • B Сортировка слиянием
  • B Быстрая сортировка
  • B Поиск в глубину (дерево)
  • B Поиск в глубину (граф)
  • B Прыжки
  • B Быстрое возведение в степень
  • A Перестановки (с повторениями и без повторений)
  • A Сочетания (с повторениями и без повторений)
• Динамическое программирование — решение общей задачи конструируется на основе ранее найденных решений подзадач
  • B Числа Фибоначчи
  • B Прыжки
  • B Поиск уникальных путей
  • B Подсчёт дождевой воды
  • B Задача о рекурсивной лестнице — подсчёт количества путей, по которым можно достичь верха лестницы
  • A Расстояние Левенштейна — метрика, измеряющая разность между двумя последовательностями
  • A Наибольшая общая подпоследовательность
  • A Наибольшая общая подстрока
  • A Наибольшая увеличивающаяся подпоследовательность
  • A Наименьшая общая суперпоследовательность
  • A Рюкзак 0-1
  • A Разбиение числа
  • A Максимальный подмассив
  • A Алгоритм Беллмана — Форда — поиск кратчайшего пути во взвешенном графе
  • A Алгоритм Флойда — Уоршелла — нахождение кратчайших путей от одной из вершин графа до всех остальных
  • A Разборщик регулярных выражений
• Поиск с возвратом (бэктрекинг) — при поиске решения многократно делается попытка расширить текущее частичное решение. Если расширение невозможно, то происходит возврат к предыдущему более короткому частичному решению, и делается попытка его расширить другим возможным способом. Обычно используется обход пространства состояний в глубину.
  • B Прыжки
  • B Поиск уникальных путей
  • B Булеан — все подмножества заданного множества
  • A Гамильтонов цикл — проходит через каждую вершину графа ровно один раз
  • A Задача об N ферзях
  • A Маршрут коня
  • A Комбинации сумм — нахождение всех комбинаций, сумма каждой из которых равна заданному числу
• Метод ветвей и границ — основан на упорядоченном переборе решений и рассмотрении только тех из них, которые являются перспективными (по тем или иным признакам) и отбрасывании бесперспективных множеств решений. Обычно используется обход в ширину в совокупности с обходом дерева пространства состояний в глубину.

Как использовать этот репозиторий

Установка всех зависимостей

npm install

Запуск ESLint

Эта команда может потребоваться вам для проверки качества кода.

npm run lint

Запуск всех тестов

npm test

Запуск определённого теста

npm test -- 'LinkedList'

Песочница

Вы можете экспериментировать с алгоритмами и структурами данных в файле ./src/playground/playground.js (файл ./src/playground/__test__/playground.test.js предназначен для написания тестов).

Для проверки работоспособности вашего кода используйте команду:

npm test -- 'playground'

Полезная информация

Ссылки

▶ О структурах данных и алгоритмах

Нотация «О» большое

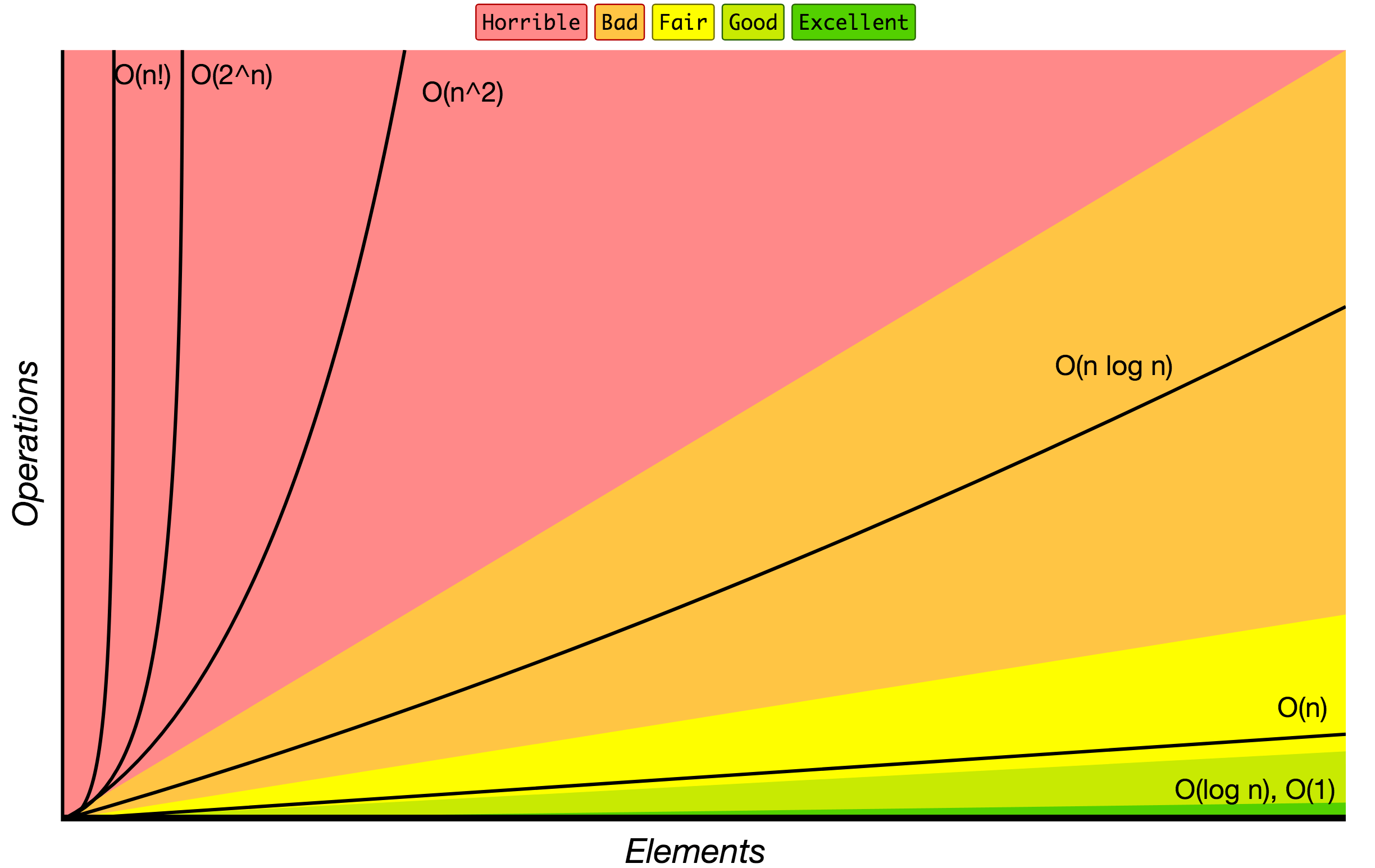
Нотация «О» большое используется для классификации алгоритмов в соответствии с ростом времени выполнения и затрачиваемой памяти при увеличении размера входных данных. На диаграмме ниже представлены общие порядки роста алгоритмов в соответствии с нотацией «О» большое.

Источник: Big O Cheat Sheet.

Ниже представлены часто используемые обозначения в нотации «О» большое, а также сравнение их производительностей на различных размерах входных данных.

Нотация «О» большое	10 элементов	100 элементов	1000 элементов
O(1)	1	1	1
O(log N)	3	6	9
O(N)	10	100	1000
O(N log N)	30	600	9000
O(N^2)	100	10000	1000000
O(2^N)	1024	1.26e+29	1.07e+301
O(N!)	3628800	9.3e+157	4.02e+2567

Сложности операций в структурах данных

Структура данных	Получение	Поиск	Вставка	Удаление	Комментарии
Массив	1	n	n	n
Стек	n	n	1	1
Очередь	n	n	1	1
Связный список	n	n	1	n
Хеш-таблица	-	n	n	n	Для идеальной хеш-функции — O(1)
Двоичное дерево поиска	n	n	n	n	В сбалансированном дереве — O(log(n))
B-дерево	log(n)	log(n)	log(n)	log(n)
Красно-чёрное дерево	log(n)	log(n)	log(n)	log(n)
АВЛ-дерево	log(n)	log(n)	log(n)	log(n)
Фильтр Блума	-	1	1	-	Возможно получение ложно-положительного срабатывания

Сложности алгоритмов сортировки

Наименование	Лучший случай	Средний случай	Худший случай	Память	Устойчивость	Комментарии
Сортировка пузырьком	n	n2	n2	1	Да
Сортировка вставками	n	n2	n2	1	Да
Сортировка выбором	n2	n2	n2	1	Нет
Сортировка кучей	n log(n)	n log(n)	n log(n)	1	Нет
Сортировка слиянием	n log(n)	n log(n)	n log(n)	n	Да
Быстрая сортировка	n log(n)	n log(n)	n2	log(n)	Нет	Быстрая сортировка обычно выполняется с использованием O(log(n)) дополнительной памяти
Сортировка Шелла	n log(n)	зависит от выбранных шагов	n (log(n))2	1	Нет
Сортировка подсчётом	n + r	n + r	n + r	n + r	Да	r — наибольшее число в массиве
Поразрядная сортировка	n * k	n * k	n * k	n + k	Да	k — длина самого длинного ключа