javascript-algorithms/README.uk-UA.md

Алгоритми JavaScript та структури даних

Даний репозиторій приклади багатьох популярних алгоритмів та структур даних на основі JavaScript.

Кожен алгоритм та структура даних має свій окремий README-файл із відповідними поясненнями та посиланнями для подальшого вивчення (включаючи посилання на відео на YouTube).

Вивчення матеріалу на інших мовах: English, 简体中文, 繁體中文, 한국어, 日本語, Polski, Français, Español, Português, Русский, Türk, Italiana, Bahasa Indonesia, Arabic, Deutsch

☝ Зверніть увагу! Даний проект призначений лише для навчальних та дослідницьких цілей, і він не призначений для виробництва (продакшн).

Структури даних

Структура даних (в програмуванні) - це спосіб організації даних в комп'ютерах. Часто разом зі структурою даних пов'язується і специфічний перелік операцій, що можуть бути виконаними над даними, організованими в таку структуру. Точніше, структура даних - це сукупність даних цінності, взаємозв'язки між ними та функції або операції, до яких можна застосувати дані.

B - Початківець, A - Просунутий рівень

• B Зв'язаний список
• B Двобічно зв'язаний список
• B Черга
• B Стек
• B Геш-таблиця
• B Купа, стіс або піраміда - max and min heap versions
• B Черга з пріоритетом
• A Префіксне дерево
• A Дерево
  • A Двійкове дерево пошуку
  • A АВЛ-дерево
  • A Червоно-чорне дерево
  • A Дерево відрізків - with min/max/sum range queries examples
  • A Дерево Фенвіка (Binary Indexed Tree)
• A Граф (абстрактний тип даних) (both directed and undirected)
• A Система неперетинних множин
• A Фільтр Блума

Алгоритми

Алгоритм - це однозначна специфікація способу вирішення класу задач. Це набір правил, які точно визначають послідовність операцій.

B - Початківець, A - Просунутий рівень

Алгоритми за тематикою

• Математика
  • B Бітова маніпуляція - встановити / отримати / оновити / очистити біти, множення / ділення на два, робити від’ємними тощо
  • B Факторіал
  • B Послідовність Фібоначчі - класична та закриті версії
  • B Основні фактори - пошук простих множників і підрахунок їх за допомогою теореми Харді-Рамануджана
  • B Тест простоти (метод пробного поділу)
  • B Алгоритм Евкліда - метод обчислення найбільшого спільного дільника (НСД)
  • B Найменше спільне кратне (НСК)
  • B Решето Ератосфена - алгоритм знаходження всіх простих чисел менших деякого цілого числа n
  • B Піднесення до степеня - перевірити, чи є число ступенем двох (просте та побітове рішення)
  • B Трикутник Паскаля
  • B Комплексне число - комплексні числа та основні операції з ними
  • B Радіани & Градуси - перетворення радіанів у градуси та навпаки
  • B Швидке піднесення до степеня
  • B Схема Горнера - поліноміальна оцінка
  • A Розбиття числа
  • A Метод дотичних (метод Ньютона) - метод наближеного знаходження кореня дійсного рівняння
  • A Алгоритм Лю Хуея - розрахунок числа π з заданою точністю методом вписаних правильних багатокутників
  • A Дискретне перетворення Фур'є - розкладання тимчасової функції (сигналу) на частотні складові
• Множина
  • B Декартів добуток множин - множина усіх можливих впорядкованих пар
  • B Тасування Фішера - Єйтса - створення випадкових перестановок кінцевого безлічі
  • A Булеан - множина всіх підмножин даної множини (бітові та зворотні рішення)
  • A Перестановка (з повтореннями та без)
  • A Комбінації (з повтореннями та без)
  • A Пошук найдовшої спільної підпослідовності
  • A Завдання пошуку найбільшою збільшується підпослідовності
  • A Найменша загальна супер-послідовність
  • A Задача пакування рюкзака - приклади "0/1" та "Необмежений"
  • A Максимальний підмасив - метод «Грубої сили» та алгоритм Кадана
  • A Комбінована сума - знайти всі комбінації, що утворюють конкретну суму
• Алгоритми роботи з рядками
  • B Відстань Геммінга - число позицій, у яких відповідні цифри двох двійкових слів однакової довжини різні
  • A Відстань Левенштейна - міра відмінності двох послідовностей символів (рядків)
  • A Алгоритм Кнута — Морріса — Пратта пошук підрядків (узгодження шаблонів)
  • A Z-функція - пошук підрядків (зіставлення зразків)
  • A Алгоритм Рабіна — Карпа - алгоритм пошуку рядка
  • A Найбільший загальний підрядок
  • A Підбирання регулярного виразу
• Алгоритми пошуку
  • B Лінійний пошук
  • B Пошук блоків - пошук у відсортованому масиві
  • B Двійковий пошук - знаходження заданого значення у впорядкованому масиві
  • B Інтерполяційний алгоритм пошуку - алгоритм для пошуку за заданим ключем в індексованому масиві, який впорядкований за значенням ключів
• Алгоритми сортування
  • B Сортування бульбашкою
  • B Сортування вибором
  • B Сортування включенням
  • B Пірамідальне сортування
  • B Сортування злиттям
  • B Швидке сортування
  • B Сортування Шелла
  • B Сортування підрахунком
  • B Сортування за розрядами
• Зв’язані списки
  • B Прямий обхід
  • B Зворотний обхід
• Дерева
  • B Пошук у глибину
  • B Пошук у ширину
• Графи
  • B Пошук у глибину
  • B Пошук у ширину
  • B Алгоритм Крускала - алгоритм побудови мінімального кістякового дерева зваженого неорієнтовного графа
  • A Алгоритм Дейкстри - знаходження найкоротшого шляху від однієї вершини графа до всіх інших вершин
  • A Алгоритм Беллмана — Форда - алгоритм пошуку найкоротшого шляху в зваженому графі
  • A Алгоритм Флойда — Воршелла - знаходження найкоротшого шляху в зваженому графі з додатними або від'ємними вагами ребер (але без від'ємнозначних циклів)
  • A Циклічний граф - граф, що складається з єдиного циклу, або, іншими словами, деякого числа вершин, з'єднаних замкнутим ланцюгом.
  • A Алгоритм Прима - жадібний алгоритм побудови мінімального кістякового дерева зваженого зв'язного неорієнтованого графа
  • A Топологічне сортування - впорядковування вершин безконтурного орієнтованого графа згідно з частковим порядком, визначеним ребрами цього графу на множині його вершин
  • A Алгоритм Тар'яна - алгоритм пошуку компонент сильної зв'язності в орієнтованому графі, що працює за лінійний час
  • A Міст (теорія графів)
  • A Ейлерів ланцюг - ланцюг у графі, який проходить кожне ребро рівно один раз
  • A Гамільтонів граф - шлях, що містить кожну вершину графа рівно один раз
  • A Компонента сильної зв'язності графа - Алгоритм Косараджу - алгоритм для знаходження компонент сильної зв’язності орієнтованого графу
  • A Задача комівояжера - знаходження найвигіднішого маршруту, що проходить через вказані міста хоча б по одному разу
• Криптографія
  • B Хеш-функція - функція, що перетворює вхідні дані будь-якого (як правило великого) розміру в дані фіксованого розміру.
  • B Шифр Цезаря (шифр зсуву) - симетричний моноалфавітний алгоритм шифрування, в якому кожна буква відкритого тексту заміняється на ту, що віддалена від неї в алфавіті на сталу кількість позицій
  • B Шифр Гілла - поліграмний шифр підстановки, заснований на лінійній алгебрі
• Машинне навчання
  • B Нано-нейрон - 7 простих функцій JS, які ілюструють, як машини насправді можуть навчатися (пряме та зворотнє поширення)
  • B Метод k-найближчих сусідів - простий непараметричний класифікаційний метод, де для класифікації об'єктів у рамках простору властивостей використовуються відстані (зазвичай евклідові), пораховані до усіх інших об'єктів
  • B Кластеризація методом к–середніх - популярний метод кластеризації, — впорядкування множини об'єктів в порівняно однорідні групи.
• Без категорії
  • B Ханойська вежа
  • B Поворот квадратної матриці
  • B Гра стрибків - зворотне відстеження, динамічне програмування (зверху вниз + знизу вгору) та жадібні приклади
  • B Проблема унікальних шляхів - зворотне відстеження, динамічне програмування та приклади на основі Трикутника Паскаля
  • B Дощові тераси - проблема захоплення дощової води (динамічне програмування та версії грубої сили)
  • B Завдання про рекурсивні сходи - підрахунок кількості способів досягти вершини (4 рішення)
  • A Задача про вісім ферзів
  • A Задача про хід коня

Парадигма програмування

Парадиигма програмува́ння — це система ідей і понять, які визначають стиль написання комп'ютерних програм, а також спосіб мислення програміста. Це спосіб концептуалізації, що визначає організацію обчислень і структурування роботи, яку виконує комп'ютер.

• Метод «грубої сили» або повний перебір - метод рішення криптографічної задачі шляхом перебору всіх можливих варіантів ключа
  • B Лінійний пошук
  • B Дощові тераси - задача про дощові тераси
  • B Завдання про рекурсивні сходи - підрахунок кількості способів досягти вершини
  • A Максимальний підмасив
  • A Задача комівояжера - знаходження найвигіднішого маршруту, що проходить через вказані міста хоча б по одному разу
  • A Дискретне перетворення Фур'є - розкладання тимчасової функції (сигналу) на частотні складові
• "Жадібні" алгоритми - простий і прямолінійний евристичний алгоритм, який приймає найкраще рішення, виходячи з наявних на кожному етапі даних, не зважаючи на можливі наслідки, сподіваючись урешті-решт отримати оптимальний розв'язок
  • B Гра стрибків - зворотне відстеження, динамічне програмування (зверху вниз + знизу вгору) та жадібні приклади
  • A Задача пакування рюкзака - приклади "0/1" та "Необмежений"
  • A Алгоритм Дейкстри - знаходження найкоротшого шляху від однієї вершини графа до всіх інших вершин
  • A Алгоритм Прима - жадібний алгоритм побудови мінімального кістякового дерева зваженого зв'язного неорієнтованого графа
  • A Алгоритм Крускала - алгоритм побудови мінімального кістякового дерева зваженого неорієнтовного графа
• Розділяй і володарюй - важлива парадигма розробки алгоритмів, що полягає в рекурсивному розбитті розв'язуваної задачі на дві або більше підзадачі того ж типу, але меншого розміру, і комбінуванні їх розв'язків для отримання відповіді до вихідного завдання. Розбиття виконуються доти, поки всі підзавдання не стануть елементарними.
  • B Двійковий пошук - знаходження заданого значення у впорядкованому масиві
  • B Ханойська вежа
  • B Трикутник Паскаля
  • B Алгоритм Евкліда - метод обчислення найбільшого спільного дільника (НСД)
  • B Сортування злиттям
  • B Швидке сортування
  • B Пошук у глибину
  • B Пошук у ширину
  • B Гра стрибків - зворотне відстеження, динамічне програмування (зверху вниз + знизу вгору) та жадібні приклади
  • B Швидке піднесення до степеня
  • A Перестановка (з повтореннями та без)
  • A Комбінації (з повтореннями та без)
• Динамічне програмування - розділ математики, який присвячено теорії і методам розв'язання багатокрокових задач оптимального управління
  • B Послідовність Фібоначчі - класична та закриті версії
  • B Гра стрибків - зворотне відстеження, динамічне програмування (зверху вниз + знизу вгору) та жадібні приклади
  • B Проблема унікальних шляхів - зворотне відстеження, динамічне програмування та приклади на основі Трикутника Паскаля
  • B Дощові тераси - проблема захоплення дощової води (динамічне програмування та версії грубої сили)
  • B Завдання про рекурсивні сходи - підрахунок кількості способів досягти вершини (4 рішення)
  • A Відстань Левенштейна - міра відмінності двох послідовностей символів (рядків)
  • A Пошук найдовшої спільної підпослідовності
  • A Найбільший загальний підрядок
  • A Завдання пошуку найбільшою збільшується підпослідовності
  • A Найменша загальна супер-послідовність
  • A Задача пакування рюкзака - приклади "0/1" та "Необмежений"
  • A Розбиття числа
  • A Максимальний підмасив
  • A Алгоритм Беллмана — Форда - алгоритм пошуку найкоротшого шляху в зваженому графі
  • A Алгоритм Флойда — Воршелла - знаходження найкоротшого шляху в зваженому графі з додатними або від'ємними вагами ребер (але без від'ємнозначних циклів)
  • A Підбирання регулярного виразу
• Пошук із зворотом - подібно до грубої сили, намагайтеся генерувати всі можливі рішення, але кожного разу, коли ви створюєте наступне рішення, тестуєте чи він задовольняє всім умовам, і лише потім продовжуєте генерувати наступні рішення. В іншому випадку поверніться назад і рухайтесь далі іншим шляхом пошуку рішення.
  • B Гра стрибків - зворотне відстеження, динамічне програмування (зверху вниз + знизу вгору) та жадібні приклади
  • B Проблема унікальних шляхів - зворотне відстеження, динамічне програмування та приклади на основі Трикутника Паскаля
  • B Булеан - множина всіх підмножин даної множини (бітові та зворотні рішення)
  • A Гамільтонів граф - шлях, що містить кожну вершину графа рівно один раз
  • A Задача про вісім ферзів
  • A Задача про хід коня
  • A Комбінована сума - знайти всі комбінації, що утворюють конкретну суму
• Метод гілок і меж - один з поширених методів дискретної оптимізації. Метод працює на дереві рішень та визначає принципи роботи конкретних алгоритмів пошуку розв'язків, тобто, є мета-алгоритмом. Для різних задач комбінаторної оптимізації створюють спеціалізовані алгоритми гілок та меж.

Як користуватися цим репозиторієм

Встановіть усі залежності

npm install

Запустіть ESLint

Запустіть для перевірки якості коду

npm run lint

Запустіть усі тести

npm test

Запустіть тести за назвою

npm test -- 'LinkedList'

Ігрище

Ви можете побавитись зі структурами даних та алгоритмами в файлі ./src/playground/playground.js та писати тести до них в даному файлі ./src/playground/__test__/playground.test.js.

Для перевірки, чи працює ваш код належним чином запустіть команду:

npm test -- 'playground'

Корисна інформація

Список літератури

▶ Структури даних та алгоритми на YouTube

Асимптотична нотація великого О (нотація Ландау)

Асимптотична нотація великого О (нотація Ландау) розповсюджена математична нотація для формального запису асимптотичної поведінки функцій. Широко вживається в теорії складності обчислень, інформатиці та математиці.

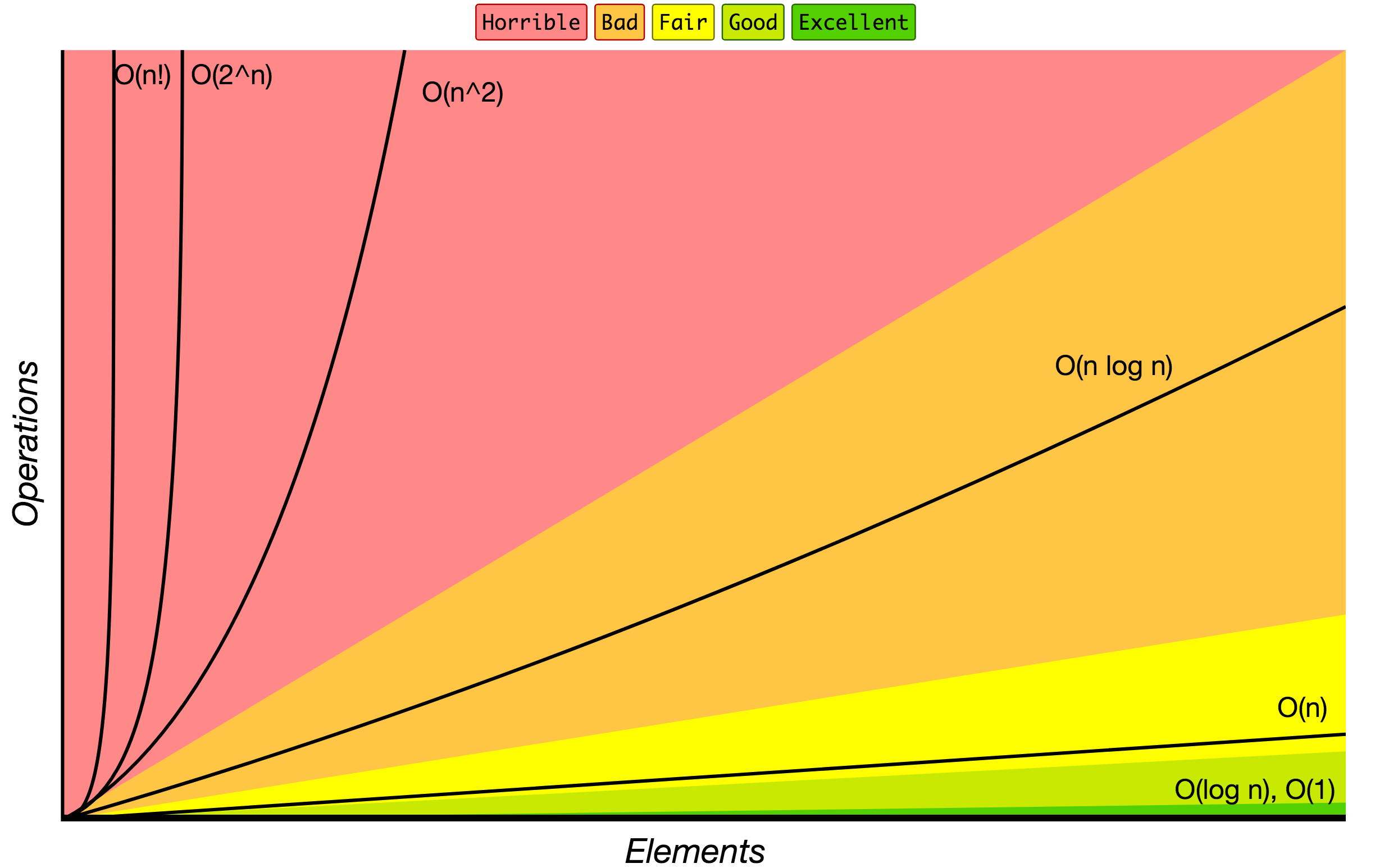
Джерело: Асимптотична нотація великого О.

Нижче наведено список деяких найбільш часто використовуваних позначень нотації Ландаута їх порівняння продуктивності з різними розмірами вхідних даних.

Нотація Ландау	Обчислення для 10 елементів	Обчислення для 100 елементів	Обчислення для 1000 елементів
O(1)	1	1	1
O(log N)	3	6	9
O(N)	10	100	1000
O(N log N)	30	600	9000
O(N^2)	100	10000	1000000
O(2^N)	1024	1.26e+29	1.07e+301
O(N!)	3628800	9.3e+157	4.02e+2567

Складність операцій в структурі даних

Структура даних	Доступ	Пошук	Вставка	Видалення	Коментарі
Масив	1	n	n	n
Купа	n	n	1	1
Черга	n	n	1	1
Зв’язаний список	n	n	1	n
Хеш-таблиця	-	n	n	n	У разі ідеальної хеш-функції - O(1)
Бінарне дерево пошуку	n	n	n	n	У разі збалансованого дерева витрати становитимуть O (log (n))
Б-дерево	log(n)	log(n)	log(n)	log(n)
Червоно-чорне дерево	log(n)	log(n)	log(n)	log(n)
АВЛ-дерево	log(n)	log(n)	log(n)	log(n)
Фільтр Блума	-	1	1	-	Під час пошуку можливі помилкові спрацьовування

Складність алгоритмів сортування масивів

Назва	Найкращий	Середній	Найгірший	Пам'ять	Стабільність	Коментарі
Сортування бульбашкою	n	n2	n2	1	Так
Сортування включенням	n	n2	n2	1	Так
Сортування вибором	n2	n2	n2	1	Ні
Пірамідальне сортування	n log(n)	n log(n)	n log(n)	1	Ні
Сортування злиттям	n log(n)	n log(n)	n log(n)	n	Так
Швидке сортування	n log(n)	n log(n)	n2	log(n)	Ні	Швидке сортування зазвичай виконується на місці з використанням O (log (n)) додаткової пам'яті
Сортування Шелла	n log(n)	залежить від послідовності проміжків	n (log(n))2	1	Ні
Сортування підрахунком	n + r	n + r	n + r	n + r	Так	Де r - найбільше число в масиві
Сортування за розрядами	n * k	n * k	n * k	n + k	Так	Де k - довжина найдовшого ключа

Патронати проекту

Ви можете підтримати цей проект через ❤️️ GitHub або ❤️️ Patreon.

Люди, які підтримують цей проект ∑ = 1

ℹ️ A few more projects and articles about JavaScript and algorithms on trekhleb.dev