javascript-algorithms/README.pe-PE.md

الگوریتم های جاوا اسکریپت و ساختارهای داده

🇺🇦 اوکراین [در حال حمله است] (https://twitter.com/MFA_Ukraine) توسط ارتش روسیه. غیرنظامیان در حال کشته شدن هستند. مناطق مسکونی در حال بمباران هستند.

• از طریق [بانک ملی اوکراین] به اوکراین کمک کنید (https://bank.gov.ua/en/news/all/natsionalniy-bank-vidkriv-spetsrahunok-dlya-zboru-koshtiv-na-potrebi-armiyi)
• از طریق صندوق SaveLife به اوکراین کمک کنید
• اطلاعات بیشتر در war.ukraine.ua

[](https://github.com/trekhleb/javascript-algorithms/actions?query=workflow% 3ACI+شاخه%3Amaster)

این مخزن شامل نمونه های بسیاری بر اساس جاوا اسکریپت است الگوریتم ها و ساختارهای داده محبوب

هر الگوریتم و ساختار داده README جداگانه خود را دارد همراه با توضیحات مرتبط و لینک برای مطالعه بیشتر (از جمله به ویدیوهای یوتیوب).

این را به زبان های دیگر بخوانید: 简体中文، 繁體中文، 한국어، 日本語، Polski، Français، Español، Português، Русский، Türk، Italiana، Bahasa Indonesia، Українська، عربی، Tiếng Việt، Deutsch

☝ توجه داشته باشید که این پروژه برای اهداف یادگیری و تحقیق استفاده می شود فقط، و نیست برای تولید استفاده شود.

ساختارهای داده

ساختار داده روشی خاص برای سازماندهی و ذخیره سازی داده ها در رایانه است تا بتواند به طور موثر قابل دسترسی و اصلاح باشد. به طور دقیق تر، ساختار داده مجموعه ای از داده ها است مقادیر، روابط بین آنها و توابع یا عملیاتی که می توان روی آنها اعمال کرد داده.

"B" - مبتدی، "A" - پیشرفته

• B [فهرست پیوند شده] (src/data-structures/linked-list)
• B [فهرست پیوند شده دوگانه] (src/data-structures/doubly-linked-list)
• 'B' [صف] (src/data-structures/queue)
• «B» [پشته] (src/data-structures/stack)
• B [Hash Table] (src/data-structures/hash-table)
• B [Heap] (src/data-structures/heap) - نسخه‌های حداکثر و حداقل پشته
• B [صف اولویت] (src/data-structures/priority-queue)
• A [Trie] (src/data-structures/trie)
• «A» [درخت] (src/data-structures/tree)
  • A [درخت جستجوی باینری] (src/data-structures/tree/binary-search-tree)
  • A [AVL Tree] (src/data-structures/tree/avl-tree)
  • A [درخت قرمز-سیاه] (src/data-structures/tree/red-black-tree)
  • A [Segment Tree] (src/data-structures/tree/segment-tree) - با نمونه جستجوهای محدوده حداقل/حداکثر/جمع
  • A درخت Fenwick (درخت نمایه شده باینری)
• A [گراف] (src/data-structures/graph) (هم جهت دار و هم بدون جهت)
• «A» [مجموعه جدا] (src/data-structures/disjoint-set)
• «A» [فیلتر بلوم] (src/data-structures/bloom-filter)

الگوریتم ها

یک الگوریتم یک مشخصات روشن از نحوه حل یک کلاس از مسائل است. این است مجموعه ای از قوانین که دقیقاً دنباله ای از عملیات را تعریف می کند.

"B" - مبتدی، "A" - پیشرفته

الگوریتم ها بر اساس موضوع

• ریاضی

  • 'B' [دستکاری بیت] (src/الگوریتم ها/ریاضی/بیت ها) - تنظیم/دریافت/به روز رسانی/پاک کردن بیت ها، ضرب/تقسیم بر دو، ایجاد منفی و غیره.
  • B [نقطه شناور دودویی] (src/الگوریتم ها/ریاضی/نقطه شناور باینری) - نمایش دودویی اعداد ممیز شناور.
  • B [فاکتوری] (src/algorithms/math/factorial)
  • 'B' [شماره فیبوناچی] (src/الگوریتم ها/ریاضی/فیبوناچی) - نسخه های کلاسیک و بسته
  • 'B' [عوامل اول] (src/الگوریتم ها/ریاضی/عوامل اول) - یافتن عوامل اول و شمارش آنها با استفاده از قضیه هاردی رامانوجان
  • B [آزمون اولیه] (src/algorithms/math/primality-test) (روش تقسیم آزمایشی)
  • 'B' [الگوریتم اقلیدسی] (src/algorithms/math/euclidean-algorithm) - محاسبه بزرگترین مقسوم علیه مشترک (GCD)
  • B [کمترین ضرب رایج] (src/algorithms/math/least-common-multiple) (LCM)
  • B [الک اراتوستن] (src/الگوریتم ها/ریاضی/الک-اراتوستن) - یافتن تمام اعداد اول تا هر حد معین
  • B [قدرت دو است] (src/algorithms/math/is-power-of-two) - بررسی کنید که آیا عدد توان دو است (الگوریتم‌های ساده و بی‌تفاوت)
  • 'B' [مثلث پاسکال] (src/algorithms/math/pascal-triangle)
  • 'B' [شماره مختلط] (src/algorithms/math/complex-number) - اعداد مختلط و عملیات اساسی با آنها
  • 'B' [رادیان و درجه] (src/الگوریتم ها/ریاضی/رادیان) - تبدیل رادیان به درجه و معکوس
  • B [تقویت سریع] (src/الگوریتم‌ها/ریاضی/تغذیه سریع)
  • B [روش هورنر] (src/الگوریتم‌ها/ریاضی/روش هورنر) - ارزیابی چند جمله‌ای
  • 'B' [ماتریس] (src/الگوریتم ها/ریاضی/ماتریس) - ماتریس ها و عملیات اصلی ماتریس (ضرب، جابجایی و غیره)
  • B [فاصله اقلیدسی](src/algorithms/

  ریاضی/اقلیدسی-فاصله) - فاصله بین دو نقطه/بردار/ماتریس

  • 'A' [پارتیشن عدد صحیح] (src/algorithms/math/integer-partition)
  • A [ریشه مربع] (src/الگوریتم ها/ریاضی/ریشه مربع) - روش نیوتن
  • A الگوریتم Liu Hui π - محاسبات π تقریبی بر اساس N-gon
  • 'A' [تبدیل فوریه گسسته] (src/algorithms/math/fourier-transform) - یک تابع زمان (یک سیگنال) را به فرکانس‌هایی که آن را تشکیل می‌دهند تجزیه می‌کند.

• مجموعه

  • B [محصول دکارتی] (src/الگوریتم‌ها/مجموعه‌ها/محصولات دکارتی) - محصول مجموعه‌های متعدد
  • 'B' [Fisher-Yates Shuffle] (src/algorithms/sets/fisher-yates) - جایگشت تصادفی یک دنباله محدود
  • «A» [مجموعه توان] (src/الگوریتم‌ها/مجموعه‌ها/مجموعه قدرت) - همه زیرمجموعه‌های یک مجموعه (راه‌حل‌های بیتی و پس‌گرد)
  • «A» [جایگشت‌ها] (src/الگوریتم‌ها/مجموعه‌ها/جایگشت‌ها) (با و بدون تکرار)
  • A [ترکیب ها] (src/الگوریتم ها/مجموعه ها/ترکیبات) (با و بدون تکرار)
  • A [طولانی ترین دنباله متداول] (src/الگوریتم ها/مجموعه ها/طولانی ترین-متداول-زیر دنباله) (LCS)
  • A [طولانی‌ترین دنباله افزایش‌دهنده] (src/الگوریتم‌ها/مجموعه‌ها/طولانی‌ترین-افزاینده-زیر دنباله)
  • A [کوتاه‌ترین سوپرست متداول] (src/الگوریتم‌ها/مجموعه‌ها/کوتاه‌ترین ابرتوالی مشترک) (SCS)
  • A [مسئله کوله پشتی] (src/algorithms/sets/knapsack-problem) - موارد "0/1" و "Unbound"
  • A [Maximum Subarray] (src/algorithms/sets/maximum-subray) - نسخه های "Brute Force" و "Dynamic Programming" (Kadane's)
  • A [ترکیب جمع] (src/الگوریتم‌ها/مجموعه‌ها/ترکیب-جمع) - همه ترکیب‌هایی را پیدا کنید که مجموع خاصی را تشکیل می‌دهند.

• رشته های

  • 'B' [فاصله همینگ] (src/الگوریتم ها/رشته/همینگ-فاصله) - تعداد موقعیت هایی که نمادها در آنها متفاوت هستند
  • B [Palindrome] (src/algorithms/string/palindrome) - بررسی کنید که آیا رشته به صورت معکوس یکسان است یا خیر
  • A [فاصله Levenshtein] (src/algorithms/string/levenshtein-distance) - حداقل فاصله ویرایش بین دو دنباله
  • A الگوریتم Knuth–Morris–Pratt (الگوریتم KMP) - جستجوی زیر رشته (تطبیق الگو)
  • A [الگوریتم Z] (src/algorithms/string/z-algorithm) - جستجوی زیر رشته (تطبیق الگو)
  • A [الگوریتم Rabin Karp] (src/algorithms/string/rabin-karp) - جستجوی زیر رشته
  • A [طولانی ترین زیر رشته مشترک] (src/algorithms/string/longest-common-substring)
  • «A» [تطبیق عبارت منظم] (src/algorithms/string/regular-expression-matching)

• جستجو

  • B [جستجوی خطی] (src/algorithms/search/linear-search)
  • B [Jump Search] (src/algorithms/search/jump-search) (یا Block Search) - جستجو در آرایه مرتب شده
  • B [جستجوی باینری] (src/algorithms/search/binary-search) - جستجو در آرایه مرتب شده
  • B [جستجوی درون یابی] (src/algorithms/search/interpolation-search) - جستجو در آرایه مرتب شده به طور یکنواخت توزیع شده

• مرتب سازی

  • «B» [مرتب‌سازی حباب‌ها] (src/الگوریتم‌ها/مرتب‌سازی/مرتب‌سازی حباب‌ها)
  • «B» [مرتب‌سازی انتخابی] (src/الگوریتم‌ها/مرتب‌سازی/مرتب‌سازی انتخابی)
  • «B» [مرتب‌سازی درج] (src/الگوریتم‌ها/مرتب‌سازی/مرتب‌سازی درج)
  • «B» [مرتب‌سازی پشته] (src/الگوریتم‌ها/مرتب‌سازی/مرتب‌سازی پشته)
  • B [Merge Sort] (src/algorithms/sorting/merge-sort)
  • «B» [مرتب‌سازی سریع] (src/الگوریتم‌ها/مرتب‌سازی/مرتب‌سازی سریع) - پیاده‌سازی در محل و غیردرجا
  • B [Sellsort] (src/algorithms/sorting/shell-sort)
  • «B» [مرتب‌سازی شمارش] (src/الگوریتم‌ها/مرتب‌سازی/شمارش مرتب‌سازی)
  • B [Radix Sort] (src/algorithms/sorting/radix-sort)

• لیست های پیوندی

  • B [پیمایش مستقیم] (src/algorithms/linked-list/traversal)
  • B [پیمایش معکوس] (src/algorithms/linked-list/reverse-traversal)

• درختان

  • B [Depth-First Search] (src/algorithms/tree/depth-first-search) (DFS)
  • B [Breadth-First Search] (src/algorithms/tree/breadth-first-search) (BFS)

• نمودارها

  • B [جستجوی عمق-اول](src/الگوریتم ها/گراف/عمق-اول-جستجو) (DFS)
  • B [جستجوی عرض-اول](src/الگوریتم ها/گراف/عرض-اول-جستجو) (BFS)
  • B [الگوریتم کروسکال] (src/algorithms/graph/kruskal) - یافتن حداقل درخت پوشا (MST) برای نمودار وزنی بدون جهت
  • A [الگوریتم Dijkstra] (src/algorithms/graph/dijkstra) - یافتن کوتاه‌ترین مسیرها به تمام رئوس نمودار از یک راس
  • A الگوریتم بلمن-فورد - یافتن کوتاه ترین مسیرها برای همه رئوس نمودار از یک راس
  • A [الگوریتم فلوید-وارشال] (src/algorithms/graph/floyd-warshall) - کوتاه ترین مسیرها را بین همه جفت رئوس پیدا کنید
  • A [Detect Cycle] (src/algorithms/graph/ detect-cycle) - هم برای نمودارهای جهت دار و هم بدون جهت (نسخه های مبتنی بر DFS و Disjoint Set)
  • A [الگوریتم Prim] (src/algorithms/graph/prim) - یافتن حداقل درخت پوشا (MST) برای نمودار وزنی بدون جهت
  • A [مرتب‌سازی توپولوژیکی] (src/algorithms/graph/topological-sorting) - روش DFS
  • A [نقاط بیانی] (src/algorithms/graph/articulation-points) - الگوریتم ترجان (بر اساس DFS)
  • A [پلها] (src/algorithms/graph/bridges) - الگوریتم مبتنی بر DFS
  • 'A' [مسیر اویلر و مدار اویلر] (src/algorithms/graph/eule

  rian-path) - الگوریتم فلوری - دقیقاً یک بار از هر لبه بازدید کنید

  • A [چرخه همیلتونی] (src/algorithms/graph/Hamiltonian-cycle) - از هر رأس دقیقاً یک بار بازدید کنید
  • A [کامپوننت های به شدت متصل] (src/algorithms/graph/strongly-connected-components) - الگوریتم کوساراجو
  • A [مسئله فروشنده مسافر] (src/algorithms/graph/travelling-salesman) - کوتاه ترین مسیر ممکن که از هر شهر بازدید می کند و به شهر مبدأ باز می گردد.

• رمزنگاری

  • B [هش چند جمله‌ای] (src/الگوریتم‌ها/رمزنگاری/هش چند جمله‌ای) - تابع هش رول بر اساس چند جمله‌ای
  • B [رمز حصار ریلی] (src/algorithms/cryptography/rail-fence-cipher) - یک الگوریتم رمز جابجایی برای رمزگذاری پیام ها
  • B [Caesar Cipher] (src/algorithms/cryptography/caesar-cipher) - رمز جایگزین ساده
  • B [رمز تپه] (src/الگوریتم‌ها/رمز نگاری/تپه-رمز) - رمز جایگزینی بر اساس جبر خطی

• فراگیری ماشین

  • B [NanoNeuron] (https://github.com/trekhleb/nano-neuron) - 7 تابع JS ساده که نشان می‌دهد ماشین‌ها چگونه واقعاً می‌توانند یاد بگیرند (انتشار به جلو/عقب)
  • B k-NN - الگوریتم طبقه‌بندی k-نزدیک‌ترین همسایگان
  • B k-Means - الگوریتم خوشه بندی k-Means

• پردازش تصویر

  • B [Seam Carving] (src/algorithms/image-processing/seam-carving) - الگوریتم تغییر اندازه تصویر آگاه از محتوا

• آمار

  • 'B' [تصادفی وزنی] (src/الگوریتم ها/آمار/وزنی-تصادفی) - آیتم تصادفی را از لیست بر اساس وزن آیتم ها انتخاب کنید

• الگوریتم های تکاملی

  • A [الگوریتم ژنتیک] (https://github.com/trekhleb/self-parking-car-evolution) - نمونه ای از نحوه استفاده از الگوریتم ژنتیک برای آموزش خودروهای خود پارکینگ

• دستهبندی نشده

  • B [برج هانوی] (src/الگوریتم‌ها/دسته‌بندی نشده/هانوی-برج)
  • B [چرخش ماتریس مربع] (src/الگوریتم‌ها/ دسته‌بندی نشده/چرخش ماتریس مربع) - الگوریتم در محل
  • B [بازی پرش] (src/الگوریتم ها/ دسته بندی نشده/بازی پرش) - عقب نشینی، برنامه نویسی پویا (از بالا به پایین + پایین به بالا) و مثال های حریصانه
  • B [مسیرهای منحصربه‌فرد] (src/الگوریتم‌ها/ دسته‌بندی‌نشده/مسیرهای منحصربه‌فرد) - بک‌تراکینگ، برنامه‌نویسی پویا و مثال‌های مبتنی بر مثلث پاسکال
  • B [تراس های بارانی] (src/الگوریتم ها/ دسته بندی نشده/تراس های بارانی) - به دام انداختن مشکل آب باران (برنامه نویسی پویا و نسخه های brute force)
  • B [پلکان بازگشتی] (src/الگوریتم‌ها/ دسته‌بندی نشده/پله‌های بازگشتی) - تعداد راه‌های رسیدن به بالا را بشمارید (4 راه‌حل)
  • B [بهترین زمان برای خرید سهام] (src/الگوریتم‌ها/دسته‌بندی نشده/بهترین زمان برای خرید-فروش- سهام) - تقسیم و غلبه و نمونه‌هایی با یک پاس
  • A [مسئله N-Queens] (src/algorithms/uncategorized/n-queens)
  • «A» [تور شوالیه] (src/الگوریتم‌ها/دسته‌بندی نشده/شوالیه-تور)

الگوریتم های پارادایم

پارادایم الگوریتمی یک روش یا رویکرد عمومی است که زیربنای طراحی یک کلاس است از الگوریتم ها این یک انتزاع بالاتر از مفهوم یک الگوریتم است، درست به عنوان یک الگوریتم یک انتزاع بالاتر از یک برنامه کامپیوتری است.

• Brute Force - به همه احتمالات نگاه کنید و بهترین راه حل را انتخاب کنید

  • B [جستجوی خطی] (src/algorithms/search/linear-search)
  • B [تراس های بارانی] (src/الگوریتم ها/ دسته بندی نشده/تراس های بارانی) - به دام انداختن مشکل آب باران
  • B [پلکان بازگشتی] (src/algorithms/uncategorized/recursive-staircase) - تعداد راه‌های رسیدن به بالا را بشمارید
  • A [حداکثر زیرآرایه] (src/algorithms/sets/maximum-subray)
  • A [مسئله فروشنده مسافر] (src/algorithms/graph/travelling-salesman) - کوتاه ترین مسیر ممکن که از هر شهر بازدید می کند و به شهر مبدأ باز می گردد.
  • 'A' [تبدیل فوریه گسسته] (src/algorithms/math/fourier-transform) - یک تابع زمان (یک سیگنال) را به فرکانس‌هایی که آن را تشکیل می‌دهند تجزیه می‌کند.

• ** حریص** - بهترین گزینه را در زمان کنونی انتخاب کنید، بدون هیچ توجهی به آینده

  • B [بازی پرش] (src/الگوریتم‌ها/ دسته‌بندی نشده/بازی پرش)
  • A [مسئله کوله پشتی بدون محدودیت] (src/algorithms/sets/knapsack-problem)
  • A [الگوریتم Dijkstra] (src/algorithms/graph/dijkstra) - یافتن کوتاهترین مسیر برای همه رئوس نمودار
  • A [الگوریتم Prim] (src/algorithms/graph/prim) - یافتن حداقل درخت پوشا (MST) برای نمودار وزنی بدون جهت
  • A [الگوریتم کروسکال] (src/algorithms/graph/kruskal) - یافتن حداقل درخت پوشا (MST) برای نمودار وزنی بدون جهت

• تقسیم و تسخیر - مسئله را به قسمت های کوچکتر تقسیم کنید و سپس آن قسمت ها را حل کنید

  • B [جستجوی باینری] (src/algorithms/search/binary-search)
  • B [برج هانوی] (src/الگوریتم‌ها/دسته‌بندی نشده/هانوی-برج)
  • 'B' [مثلث پاسکال] (src/algorithms/math/pascal-triangle)
  • 'B' [الگوریتم اقلیدسی] (src/algorithms/math/euclidean-algorithm) - محاسبه بزرگترین مقسوم علیه مشترک (GCD)
  • B [Merge Sort] (src/algorithms/sorting/merge-sort)
  • «B» [مرتب‌سازی سریع] (src/الگوریتم‌ها/مرتب‌سازی/مرتب‌سازی سریع)
  • B [جستجوی اول عمق درخت] (src/algorithms/tree/depth-first-search) (DFS)
  • B [عمق نمودار-F

  irst Search](src/algorithms/graph/depth-first-search) (DFS)

  • B [ماتریس] (src/الگوریتم ها/ریاضی/ماتریس) - تولید و پیمایش ماتریس های اشکال مختلف
  • B [بازی پرش] (src/الگوریتم‌ها/ دسته‌بندی نشده/بازی پرش)
  • B [تقویت سریع] (src/الگوریتم‌ها/ریاضی/تغذیه سریع)
  • B [بهترین زمان برای خرید سهام] (src/الگوریتم‌ها/دسته‌بندی نشده/بهترین زمان برای خرید-فروش- سهام) - تقسیم و غلبه و نمونه‌هایی با یک پاس
  • «A» [جایگشت‌ها] (src/الگوریتم‌ها/مجموعه‌ها/جایگشت‌ها) (با و بدون تکرار)
  • A [ترکیب ها] (src/الگوریتم ها/مجموعه ها/ترکیبات) (با و بدون تکرار)
  • A [حداکثر زیرآرایه] (src/algorithms/sets/maximum-subray)

• برنامه نویسی پویا - ایجاد راه حل با استفاده از راه حل های فرعی که قبلاً پیدا شده بود

  • 'B' [شماره فیبوناچی] (src/الگوریتم ها/ریاضی/فیبوناچی)
  • B [بازی پرش] (src/الگوریتم‌ها/ دسته‌بندی نشده/بازی پرش)
  • B [مسیرهای منحصر به فرد] (src/algorithms/uncategorized/unique-paths)
  • B [تراس های بارانی] (src/الگوریتم ها/ دسته بندی نشده/تراس های بارانی) - به دام انداختن مشکل آب باران
  • B [پلکان بازگشتی] (src/algorithms/uncategorized/recursive-staircase) - تعداد راه‌های رسیدن به بالا را بشمارید
  • B [Seam Carving] (src/algorithms/image-processing/seam-carving) - الگوریتم تغییر اندازه تصویر آگاه از محتوا
  • A [فاصله Levenshtein] (src/algorithms/string/levenshtein-distance) - حداقل فاصله ویرایش بین دو دنباله
  • A [طولانی ترین دنباله متداول] (src/الگوریتم ها/مجموعه ها/طولانی ترین-متداول-زیر دنباله) (LCS)
  • A [طولانی ترین زیر رشته مشترک] (src/algorithms/string/longest-common-substring)
  • A [طولانی‌ترین دنباله افزایش‌دهنده] (src/الگوریتم‌ها/مجموعه‌ها/طولانی‌ترین-افزاینده-زیر دنباله)
  • A [کوتاه‌ترین سوپرست متداول] (src/الگوریتم‌ها/مجموعه‌ها/کوتاه‌ترین سوپرتوالی مشترک)
  • A [0/1 مشکل کوله پشتی] (src/algorithms/sets/knapsack-problem)
  • 'A' [پارتیشن عدد صحیح] (src/algorithms/math/integer-partition)
  • A [حداکثر زیرآرایه] (src/algorithms/sets/maximum-subray)
  • A [الگوریتم بلمن-فورد] (src/algorithms/graph/bellman-ford) - یافتن کوتاه ترین مسیر برای همه رئوس نمودار
  • A [الگوریتم فلوید-وارشال] (src/algorithms/graph/floyd-warshall) - کوتاه ترین مسیرها را بین همه جفت رئوس پیدا کنید
  • «A» [تطبیق عبارت منظم] (src/algorithms/string/regular-expression-matching)

• Backtracking - مشابه نیروی بی رحم، سعی کنید همه راه حل های ممکن را ایجاد کنید، اما هر بار که راه حل بعدی را ایجاد می کنید، آزمایش می کنید اگر همه شرایط را برآورده کند و تنها پس از آن به تولید راه حل های بعدی ادامه دهید. در غیر این صورت، به عقب برگردید، و ادامه دهید مسیرهای مختلف برای یافتن راه حل به طور معمول از پیمایش DFS فضای حالت استفاده می شود.

  • B [بازی پرش] (src/الگوریتم‌ها/ دسته‌بندی نشده/بازی پرش)
  • B [مسیرهای منحصر به فرد] (src/algorithms/uncategorized/unique-paths)
  • «B» [مجموعه توان] (src/الگوریتم‌ها/ست‌ها/مجموعه قدرت) - همه زیر مجموعه‌های یک مجموعه
  • A [چرخه همیلتونی] (src/algorithms/graph/Hamiltonian-cycle) - از هر رأس دقیقاً یک بار بازدید کنید
  • A [مسئله N-Queens] (src/algorithms/uncategorized/n-queens)
  • «A» [تور شوالیه] (src/الگوریتم‌ها/دسته‌بندی نشده/شوالیه-تور)
  • A [ترکیب جمع] (src/الگوریتم‌ها/مجموعه‌ها/ترکیب-جمع) - همه ترکیب‌هایی را پیدا کنید که مجموع خاصی را تشکیل می‌دهند.

• **شاخه و محدود ** - کم هزینه ترین راه حل یافت شده در هر مرحله از عقب نشینی را به خاطر بسپارید جستجو کنید، و از هزینه کم‌هزینه‌ترین راه‌حلی که تاکنون پیدا شده است، به عنوان یک کران پایین‌تر در هزینه استفاده کنید یک راه حل کم هزینه برای مشکل، به منظور کنار گذاشتن راه حل های جزئی با هزینه های بیشتر از این کم هزینه ترین راه حل پیدا شده تا کنون به طور معمول پیمایش BFS در ترکیب با پیمایش DFS فضای حالت درخت استفاده می شود

نحوه استفاده از این مخزن

همه وابستگی ها را نصب کنید

npm نصب کنید

اجرای ESLint

ممکن است بخواهید آن را اجرا کنید تا کیفیت کد را بررسی کنید.

npm اجرا lint

اجرای تمام تست ها

تست npm

آزمون ها را با نام اجرا کنید

تست npm -- 'LinkedList'

عیب یابی

اگر پرده زدن یا آزمایش ناموفق بود، سعی کنید پوشه «node_modules» را حذف کنید و بسته‌های npm را دوباره نصب کنید:

rm -rf ./node_modules
npm من

همچنین مطمئن شوید که از نسخه صحیح Node (>=14.16.0) استفاده می کنید. اگر از nvm برای مدیریت نسخه Node استفاده می‌کنید، می‌توانید «nvm use» را از پوشه اصلی پروژه اجرا کنید و نسخه صحیح انتخاب خواهد شد.

زمین بازی

می‌توانید با ساختارهای داده و الگوریتم‌ها در فایل «./src/playground/playground.js» بازی کنید و بنویسید آن را در «./src/playground/test/playground.test.js» آزمایش می کند.

سپس به سادگی دستور زیر را اجرا کنید تا بررسی کنید که آیا کد زمین بازی شما مطابق انتظار کار می کند یا خیر:

تست npm -- "زمین بازی"

اطلاعات مفید

منابع

▶ ساختارها و الگوریتم‌های داده در YouTube

نماد بزرگ O

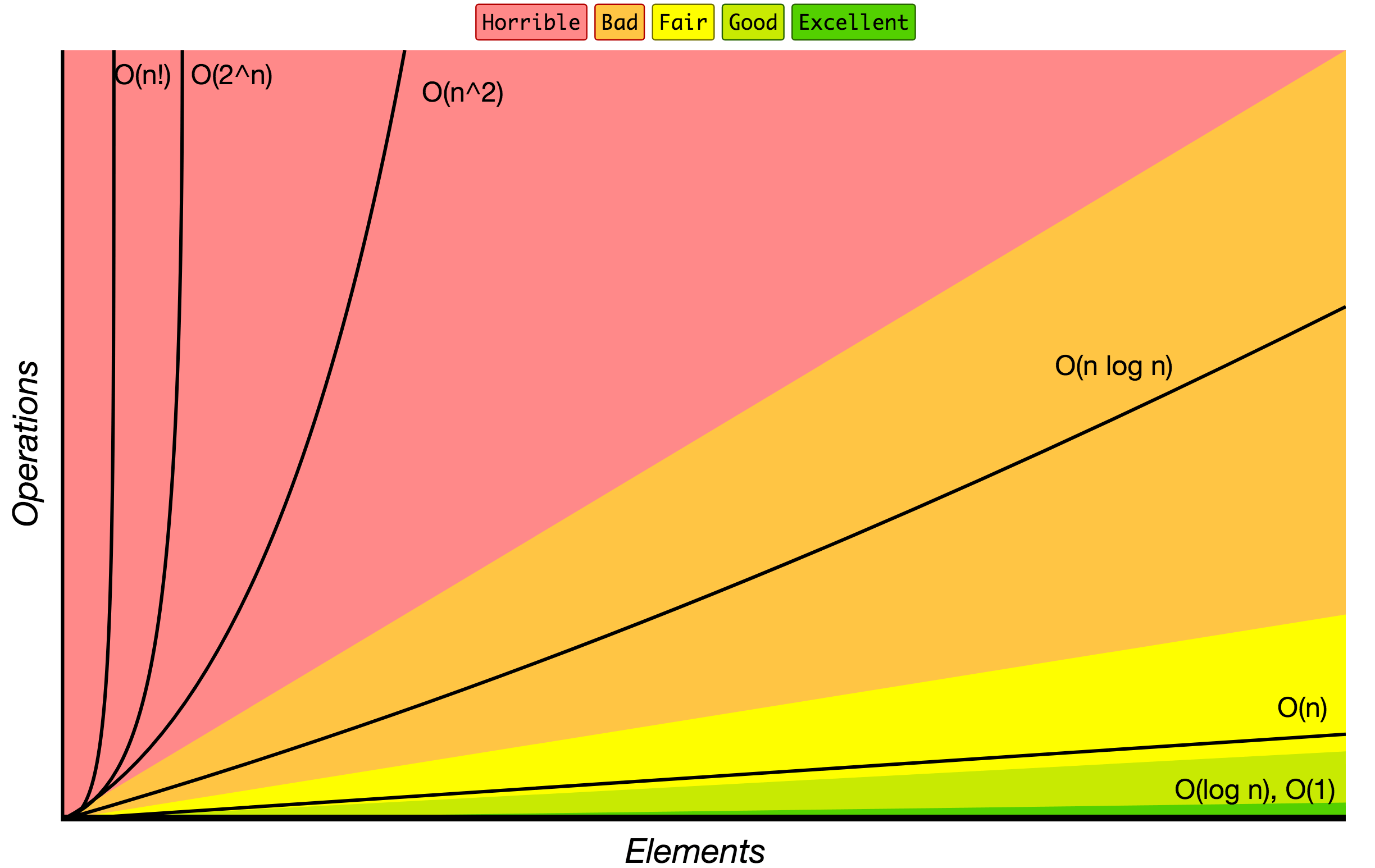
نشانگذاری Big O برای طبقه بندی الگوریتم ها بر اساس چگونگی رشد زمان یا فضای مورد نیاز آنها با افزایش اندازه ورودی استفاده می شود. در نمودار زیر می توانید رایج ترین ترتیبات رشد الگوریتم های مشخص شده را بیابید

در نماد O بزرگ.

منبع: Big O Cheat Sheet.

در زیر لیستی از برخی از پرکاربردترین نمادهای Big O و مقایسه عملکرد آنها در برابر اندازه های مختلف داده های ورودی آورده شده است.

Big O Notation	نوع	محاسبات برای 10 عنصر	محاسبات برای 100 عنصر	محاسبات برای 1000 عنصر
O(1)	ثابت	1	1	1
O(log N)	لگاریتمی	3	6	9
O(N)	خطی	10	100	1000
O(N log N)	n log(n)	30	600	9000
O(N^2)	درجه دوم	100	10000	1000000
O(2^N)	نمایی	1024	1.26e+29	1.07e+301
O(N!)	فاکتوریل	3628800	9.3e+157	4.02e+2567

پیچیدگی عملیات ساختار داده

ساختار داده	دسترسی	جستجو	درج	حذف	نظرات
آرایه	1	n	n	n
پشته	n	n	1	1
**صف **	n	n	1	1
فهرست پیوند شده	n	n	1	n
جدول هش	-	n	n	n	در صورت عملکرد هش کامل هزینه ها O(1)
درخت جستجوی باینری	n	n	n	n	در صورت متعادل بودن هزینه های درخت O(log(n))
B-Tree	log(n)	log(n)	log(n)	log(n)
درخت قرمز-سیاه	log(n)	log(n)	log(n)	log(n)
AVL Tree	log(n)	log(n)	log(n)	log(n)
فیلتر بلوم	-	1	1	-	در حین جستجو، نتایج مثبت کاذب امکان پذیر است

پیچیدگی الگوریتم های مرتب سازی آرایه

نام	بهترین	میانگین	بدترین	حافظه	پایدار	نظرات
مرتب سازی حبابی	n	n2	n2	1	بله
**مرتب سازی درج **	n	n2	n2	1	بله
مرتب سازی انتخابی	n2	n2	n2	1	نه
مرتب سازی پشته	n log(n)	n log(n)	n log(n)	1	نه
**مرتب سازی ادغام **	n log(n)	n log(n)	n log(n)	n	بله
مرتب سازی سریع	n log(n)	n log(n)	n2	log(n)	نه	مرتب سازی سریع معمولاً در محل با فضای پشته O(log(n)) انجام می شود
مرتب سازی پوسته	n log(n)	به دنباله شکاف بستگی دارد	n (log(n))2	1	نه
شمارش مرتب سازی	n + r	n + r	n + r	n + r	بله	r - بزرگترین عدد در آرایه
مرتب سازی ریشه	n * k	n * k	n * k	n + k	بله	k - طول طولانی ترین کلید

حامیان پروژه

می توانید از طریق ❤️️ GitHub یا ❤️️ [Patreon] (https://www.patreon.com/trekhleb) از این پروژه حمایت کنید.

کسانی که از این پروژه حمایت می کنند ∑ = 0

ℹ️ چند پروژه و مقاله دیگر درباره جاوا اسکریپت و الگوریتم ها در [trekhleb.dev](https:/ /trekhleb.dev)