hxx/javascript-algorithms
1
0
Fork 0
mirror of https://github.moeyy.xyz/https://github.com/trekhleb/javascript-algorithms.git synced 2024-11-10 11:09:43 +08:00
Code Issues Packages Projects Releases Wiki Activity
c539d21589
javascript-algorithms/README.ma-MA.md
name 7e8d5689ab deploy
2022-08-25 16:41:58 -07:00

23 KiB
Raw Blame History

Algoritma JavaScript dan Struktur Data

🇺🇦 UKRAINE SEDANG DISERANG OLEH TENTERA RUSIA. ORANG AWAM SEMAKIN DIBUNUH. KAWASAN KEDIAMAN SEMAKIN DIBOM.

[CI](https://github.com/trekhleb/javascript-algorithms/actions?query=workflow% 3ACI+cawangan%3Amaster) codecov

Repositori ini mengandungi banyak contoh berasaskan JavaScript algoritma dan struktur data yang popular.

Setiap algoritma dan struktur data mempunyai README tersendiri dengan penjelasan dan pautan berkaitan untuk bacaan lanjut (termasuk yang kepada video YouTube).

Baca ini dalam bahasa lain: 简体中文, 繁體中文, 한국어, 日本語, Polski, Français, Español, Português, Русский, Türk, Italiana, Bahasa Indonesia, Українська, Arab, Tiếng Việt, Deutsch

☝ Ambil perhatian bahawa projek ini bertujuan untuk digunakan untuk tujuan pembelajaran dan penyelidikan sahaja, dan ia tidak bertujuan untuk digunakan untuk pengeluaran.

Struktur Data

Struktur data ialah cara tertentu untuk mengatur dan menyimpan data dalam komputer supaya ia boleh boleh diakses dan diubah suai dengan cekap. Lebih tepat lagi, struktur data ialah himpunan data nilai, hubungan di antara mereka, dan fungsi atau operasi yang boleh digunakan data itu.

B - Pemula, A - Lanjutan

Algoritma

Algoritma ialah spesifikasi yang tidak jelas tentang cara menyelesaikan kelas masalah. Ia adalah satu set peraturan yang mentakrifkan dengan tepat urutan operasi.

B - Pemula, A - Lanjutan

Algoritma mengikut Topik

Algoritma mengikut Paradigma

Paradigma algoritma ialah kaedah atau pendekatan generik yang mendasari reka bentuk kelas daripada algoritma. Ia adalah abstraksi yang lebih tinggi daripada tanggapan algoritma, sama seperti an algoritma adalah abstraksi yang lebih tinggi daripada program komputer.

  • Brute Force - lihat semua kemungkinan dan pilih penyelesaian terbaik
    • B Carian Linear
    • B Rain Terraces - memerangkap masalah air hujan
    • B [Tangga Rekursif](src/algoritma/tak berkategori/tangga rekursif) - kira bilangan cara untuk sampai ke atas
    • A [Subarray Maksimum](src/algoritma/set/subarray maksimum)
    • A Masalah Jurujual Perjalanan - laluan terpendek mungkin yang melawati setiap bandar dan kembali ke bandar asal
    • A Transformasi Fourier Diskret - menguraikan fungsi masa (suatu isyarat) kepada frekuensi yang membentuknya
  • Rakus - pilih pilihan terbaik pada masa semasa, tanpa sebarang pertimbangan untuk masa hadapan
  • B [Permainan Lompat](src/algoritma/tidak dikategorikan/permainan lompat)
  • Divide and Conquer - bahagikan masalah kepada bahagian yang lebih kecil dan kemudian selesaikan bahagian tersebut
  • Pengaturcaraan Dinamik - bina penyelesaian menggunakan sub-penyelesaian yang ditemui sebelum ini
  • Penjejakan Belakang - sama seperti kekerasan, cuba jana semua penyelesaian yang mungkin, tetapi setiap kali anda menjana penyelesaian seterusnya anda menguji jika ia memenuhi semua syarat, dan hanya kemudian terus menjana penyelesaian seterusnya. Jika tidak, mundur, dan teruskan a jalan yang berbeza untuk mencari penyelesaian. Biasanya traversal DFS bagi ruang keadaan sedang digunakan.

    • B [Permainan Lompat](src/algoritma/tidak dikategorikan/permainan lompat)

    • B [Laluan Unik](src/algoritma/tidak dikategorikan/laluan-unik)

    • B Set Kuasa - semua subset set

    • A Kitaran Hamiltonian - Lawati setiap bucu tepat sekali

    • A Masalah N-Queens

    • A [Lawatan Kesatria](src/algoritma/tidak dikategorikan/jelajah kesatria)

    • A Jumlah Gabungan - cari semua gabungan yang membentuk jumlah tertentu

    • Branch & Bound - ingat penyelesaian kos terendah yang terdapat pada setiap peringkat penjejakan ke belakang cari, dan gunakan kos penyelesaian kos terendah yang ditemui setakat ini sebagai had yang lebih rendah pada kos penyelesaian kos termurah untuk masalah, untuk membuang penyelesaian separa dengan kos lebih besar daripada penyelesaian kos terendah ditemui setakat ini. Biasanya traversal BFS digabungkan dengan traversal DFS of state-space pokok sedang digunakan.

Cara menggunakan repositori ini

Pasang semua kebergantungan

pemasangan npm

Jalankan ESLint

Anda mungkin mahu menjalankannya untuk menyemak kualiti kod.

npm run lint

Jalankan semua ujian

ujian npm

Jalankan ujian mengikut nama

ujian npm -- 'LinkedList'

Penyelesaian masalah

Jika linting atau ujian gagal, cuba padamkan folder node_modules dan pasang semula pakej npm:

rm -rf ./node_modules
npm i

Juga pastikan anda menggunakan versi Nod yang betul (>=14.16.0). Jika anda menggunakan nvm untuk pengurusan versi Nod, anda boleh menjalankan nvm use daripada folder akar projek dan versi yang betul akan diambil.

Taman permainan

Anda boleh bermain dengan struktur data dan algoritma dalam fail ./src/playground/playground.js dan tulis mengujinya dalam ./src/playground/__test__/playground.test.js.

Kemudian hanya jalankan arahan berikut untuk menguji sama ada kod taman permainan anda berfungsi seperti yang diharapkan:

ujian npm -- 'taman permainan'

Informasi berguna

Rujukan

▶ Struktur Data dan Algoritma di YouTube

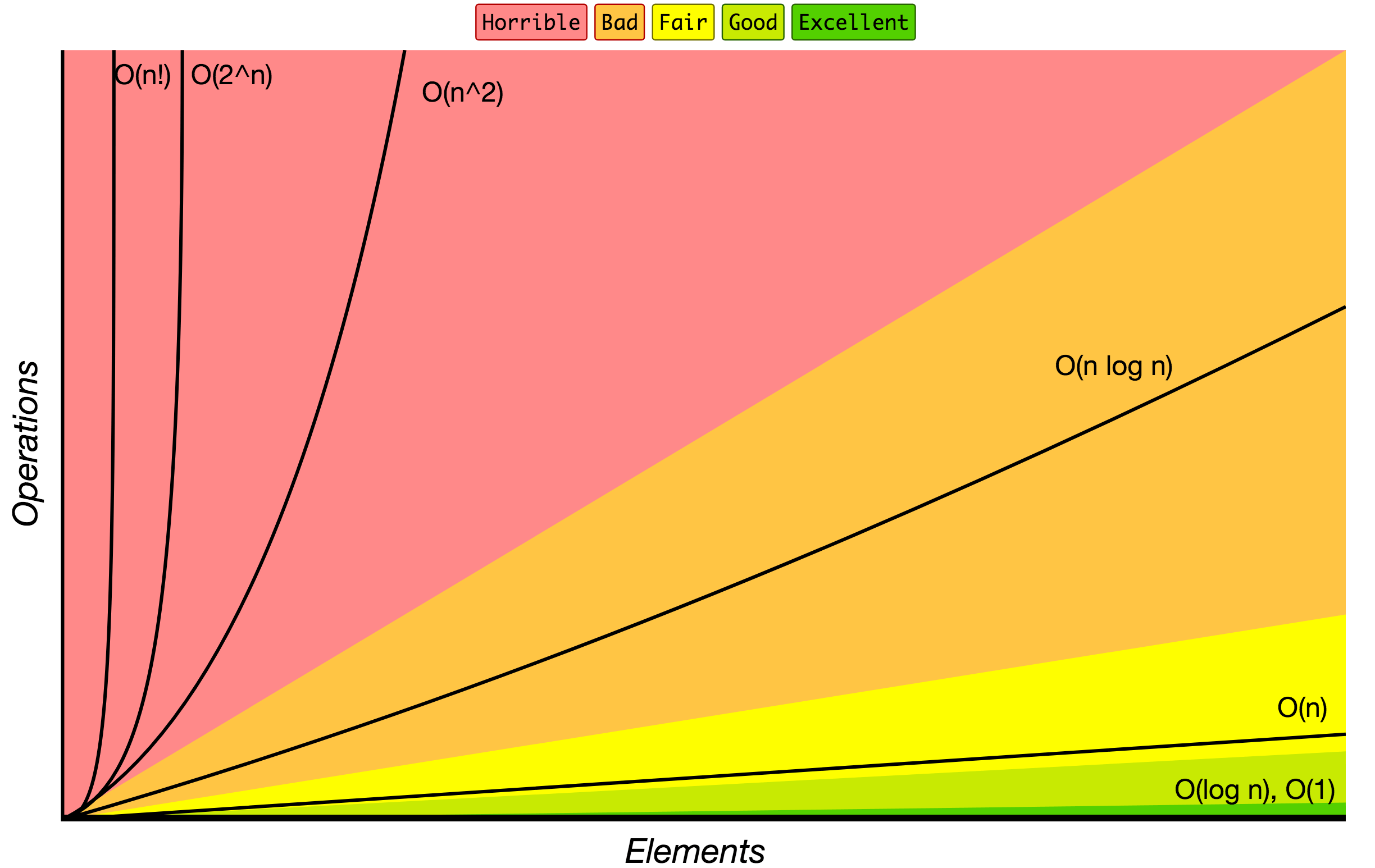
Notasi O Besar

Notasi O Besar digunakan untuk mengklasifikasikan algoritma mengikut cara masa berjalan atau keperluan ruang mereka berkembang apabila saiz input bertambah. Pada carta di bawah anda mungkin menemui susunan pertumbuhan algoritma yang paling biasa yang dinyatakan dalam tatatanda Big O.

Graf O Besar

Sumber: Big O Cheat Sheet.

Di bawah ialah senarai beberapa tatatanda Big O yang paling banyak digunakan dan perbandingan prestasinya terhadap saiz data input yang berbeza.

Notasi O Besar Taip Pengiraan untuk 10 elemen Pengiraan untuk 100 elemen Pengiraan untuk 1000 elemen
O(1) Malar 1 1 1
O(log N) Logaritma 3 6 9
O(N) Linear 10 100 1000
O(N log N) n log(n) 30 600 9000
O(N^2) Kuadratik 100 10000 1000000
O(2^N) Eksponen 1024 1.26e+29 1.07e+301
O(N!) Faktorial 3628800 9.3e+157 4.02e+2567

Kerumitan Operasi Struktur Data

Struktur Data Akses Cari Sisipan Pemadaman Komen
Array 1 n n n
Timbunan n n 1 1
Beratur n n 1 1
Senarai Terpaut n n 1 n
Jadual Hash - n n n Dalam kes kos fungsi cincang yang sempurna ialah O(1)
Pokok Carian Binari n n n n Dalam kes kos pokok seimbang ialah O(log(n))
B-Tree log(n) log(n) log(n) log(n)
Pokok Merah-Hitam log(n) log(n) log(n) log(n)
Pokok AVL log(n) log(n) log(n) log(n)
Penapis Bloom - 1 1 - Positif palsu mungkin semasa mencari

Kerumitan Algoritma Pengisihan Tatasusunan

Nama Terbaik Purata Paling teruk Memori Stabil Komen
Isih gelembung n n2 n2 1 Ya
Isihan sisipan n n2 n2 1 Ya
Isih pilihan n2 n2 n2 1 Tidak
Isihan timbunan n log(n) n log(n) n log(n) 1 Tidak
Isih gabung n log(n) n log(n) n log(n) n Ya
Isih cepat n log(n) n log(n) n2 log(n) Tidak Quicksort biasanya dilakukan di tempat dengan ruang tindanan O(log(n))
Isih cangkerang n log(n) bergantung pada jujukan jurang n (log(n))2 1 Tidak
Isih mengira n + r n + r n + r n + r Ya r - nombor terbesar dalam tatasusunan
Isih Radix n * k n * k n * k n + k Ya k - panjang kunci terpanjang

Penyokong Projek

Anda boleh menyokong projek ini melalui ❤️️ GitHub atau ❤️️ Patreon.

Orang yang menyokong projek ini ∑ = 0

ℹ️ Beberapa lagi projek dan artikel tentang JavaScript dan algoritma pada [trekhleb.dev](https:/ /trekhleb.dev)